ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Переменный электрический ток – это электрический ток, изменяющийся во времени. К переменному току относят различные виды импульсных, пульсирующих периодических и квазипериодических токов. В технике под переменным током обычно подразумевают периодические токи переменного направления. Чаще всего применяется переменный ток, сила которого меняется во времени по гармоническому закону (гармонический, или синусоидальный переменный ток).
Рассмотрим процессы, происходящие в цепях, по которым протекает переменный гармонический ток. Предположим, что режим прохождения тока установился, т.е. собственные колебания в цепи затухли, и физические процессы в цепи представляют собой вынужденные колебания. Такие предположения позволяют избежать математических трудностей, связанных с решением дифференциальных уравнений, и существенно упростить анализ процессов происходящих в цепях переменного тока.
Рассмотрим частные случаи, когда переменное напряжение U(t) = U0·coswt подается или на сопротивление R, или на емкость C, или на индуктивность L.
Сопротивление R
Если в качестве нагрузки выступает активное сопротивление R, то ток в цепи определяется соотношением:
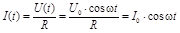
|
Видно, что в такой цепи колебание тока происходит синфазно с колебаниями напряжения, без сдвига по фазе между напряжением и током. Амплитудные значения тока и напряжения связаны соотношением
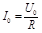 . .
| (14) |
Емкость С
Если цепь состоит только из емкости C, то изменение тока со временем определяется скоростью изменения заряда конденсатора I = dq/dt. Так как q = C·U(t), то
 , ,
| (15) |
где I0 = w·C·U0.
То есть ток в цепи, состоящей только из емкости, изменяется со временем, так же как и напряжение, по синусоиде, но опережает по фазе напряжение на 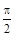 . Временнáя зависимость напряжения и силы тока в такой цепи представлена на рис. 15.
. Временнáя зависимость напряжения и силы тока в такой цепи представлена на рис. 15.
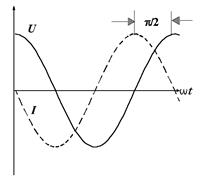
Рис. 15.
Кроме того, видно, что если ввести понятие емкостного сопротивления 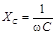 , то амплитудные значения напряжения U0 и тока I0 связаны законом Ома
, то амплитудные значения напряжения U0 и тока I0 связаны законом Ома
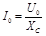 . .
| (16) |
Сдвиг по фазе можно объяснить следующим образом. Возьмем заряженный конденсатор, который начинает разряжаться. Это значит, что напряжение начинает убывать, а ток - увеличиваться по абсолютной величине. Когда напряжение на обкладках конденсатора окажется равным нулю, ток достигнет максимума. Далее происходит изменение знака напряжения, что соответствует перезарядке конденсатора. После чего напряжение по абсолютной величине начинает увеличиваться, а сила тока уменьшаться. Описанные процессы иллюстрируют возникновение сдвига по фазе между напряжением и силой тока на 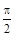 .
.
Индуктивность L
Пусть через катушку (соленоид), характеризующуюся постоянной самоиндукции (или индуктивностью) L, проходит переменный ток I(t) = I0·coswt.
По закону электромагнитной индукции (Фарадея - Ленца) в любом замкнутом контуре при изменении магнитного потока через поверхность (площадь), ограниченную этим контуром, возникает ЭДС индукции E, пропорциональная скорости изменения магнитного потока
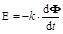 , ,
|
где Φ – магнитный поток, k – коэффициент (в системе СИ k = 1). Знак «минус» означает, что направление индукционного тока таково, что создаваемое им магнитное поле препятствует изменению первичного магнитного потока.
Частным случаем проявления этого эффекта является возникновение самоиндукции при любых изменениях тока в цепи. В простейшем случае (при отсутствии ферромагнетиков) Φ = L·I, где L – индуктивность проводника, зависящая от его размеров, формы и свойств среды. Изменения тока вызывают изменения создаваемого им магнитного потока, что в свою очередь приводит к появлению ЭДС самоиндукции E, равной
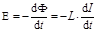 . .
|
ЭДС самоиндукции в цепи, состоящей из соленоида, в каждый момент времени компенсируется напряжением U, подаваемым на индуктивность L. То есть
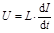 . .
| (17) |
Тогда
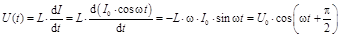 , ,
| (18) |
где U0 = w·L·I0.
Формула (18) показывает, что напряжение в цепи опережает ток на 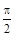 .
.
Если ввести понятие индуктивного сопротивления XL = w·L, то амплитудные значения напряжения и силы тока можно связать законом Ома:
 . .
| (19) |
Согласно (14), (16) и (19) закон Ома справедлив для амплитудных значений напряжения и тока.
Закон Ома для мгновенных значений переменного тока можно использовать только для случая активного сопротивления R.
Величину переменного тока можно охарактеризовать амплитудными значениями тока или напряжения. Это целесообразно делать, например, при подборе изоляции каких-либо электротехнических деталей, так как «пробои» возникают именно в моменты, когда переменное напряжение достигает максимальных значений.
На практике обычно вводят понятие эффективных (действующих) значения величин силы тока Iэфф и напряжения Uэфф, чтобы формула для поглощаемой (отдаваемой сопротивлению) мощности имела тот же вид, что и для цепей постоянного тока[1]:
 , ,
| (20) | |
 . .
| (21) |
Тогда
| P = Iэфф·Uэфф·cosφ. | (22) |
Легко показать, что эффективное значение переменного тока Iэфф равно такому значению постоянного тока I, который выделяет на
сопротивлении R за одно и то же время t столько же тепла Q, что и данный переменный ток.
В обозначениях переменного напряжения U, и силы тока I, под U и I обычно понимают эффективные значения тока и напряжения. Напряжение сети переменного тока «220В» является именно эффективным напряжением, и именно эффективные значения тока и напряжения измеряют амперметры и вольтметры.
ПОНЯТИЕ О ВЕКТОРНЫХ ДИАГРАММАХ
Реальные электрические цепи представляют какие-либо комбинации простейших элементов R, C и L.
Чтобы определить связь между током и напряжением в цепи, включающей несколько различных элементов, необходимо уметь складывать гармонические колебания одной частоты, но с разными амплитудами и фазами. Такую задачу аналитически бывает решить сложно, но существует графический метод, позволяющий сделать это достаточно просто и наглядно, – это метод векторных диаграмм.
 |
Данный метод основан на том, что изменяющуюся по гармоническому закону величину, например, a(t) = A0·sin(wt + j) (или a(t) = A0·cos(wt + j)), можно представить как проекцию на ось ординат (или ось абсцисс) радиус-вектора, вращающегося против часовой стрелки с угловой скоростью w (рис. 16) – a1 = A0·sinωt1, a2 = A0·sinωt2.
Рис. 16.
Длина такого вектора должна быть равна амплитуде колебаний, т.е. в данном случае равна A01. Начальное его положение при t = 0 должно составлять с осью X угол j (j – начальная фаза колебаний). Совокупность нескольких векторов, изображающих гармонически изменяющиеся величины одной и той же частоты называется векторной диаграммой.
Взаимная ориентация векторов сохраняется в любой момент времени, если складываемые колебания имеют одну и ту же частоту, поэтому для построения векторных диаграмм токов и напряжений достаточно указать их фазовые углы в момент t = 0.
 |
При построении векторных диаграмм используется математическая теорема, согласно которой проекция геометрической суммы векторов на любую ось равна алгебраической сумме их проекций на ту же ось. Поэтому задача сложения выражений типа U(t) = U0·sin(wt + j) сводится к простой графической задаче сложения векторов (рис. 17 – u1 = U10·sinφ1, u2 = U20·sinφ2, u = u1 + u2 = U0·sinφ).[2]
Рис. 17.
Последовательное соединение элементов
Рассмотрим последовательное соединение емкости, индуктивности и активного сопротивления, к которым приложено переменное напряжение U(t) = U0·coswt (рис. 18).
В случае последовательного соединения в каждый момент времени сила тока во всех участках цепи одна и та же, а сумма мгновенных падений напряжения на элементах равна значению приложенного к цепи напряжения в тот же момент времени:
| U(t) = UR(t) + UC(t) + UL(t). | (23) |
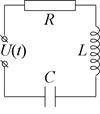
Рис. 18.
Представим соотношение (23) в виде векторной диаграммы и с ее помощью найдем связь между амплитудными и мгновенными значениями тока и напряжения в рассматриваемой цепи.
 а
а
|  б
б
|
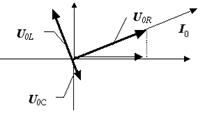
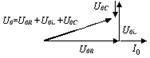
| Рис. 19. |
UR совпадает по фазе с током, значит, вектор U0R направлен так же как вектор I0, UC отстает от тока на p/2, значит, U0C развернут на p/2 «назад» относительно U0R, а U0L, соответственно «вперед» (рис. 19,а). Поскольку эти векторы вращаются с одной частотой w против часовой стрелки, то их взаимное расположение друг относительно друга не изменяется, и найти суммарное напряжение U0 можно в любой момент времени (рис. 19,б).
Из рис. 19,б видно, что
| U02 = U0R2 + (U0L – U0C)2, | (24) |
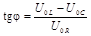 , ,
| (25) |
где j – угол между векторами I0 и U0.
Воспользовавшись формулами (14), (16) и (19) можно вместо (24) и (25) записать:
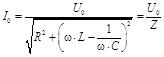 , ,
| (26) |
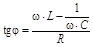 . .
| (27) |
Величина 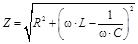 называется полным сопротивлением цепи или импедансом, а формула (26) - обобщенным законом Ома. По аналогии с треугольником, образуемым амплитудными значениями падений напряжения, можно построить треугольник сопротивлений (рис. 20) Графически полное сопротивление будет представлять собой гипотенузу прямоугольного треугольника. Один катет такого треугольника равен R – его называют активным сопротивлением. Другой катет равен (w·L –
называется полным сопротивлением цепи или импедансом, а формула (26) - обобщенным законом Ома. По аналогии с треугольником, образуемым амплитудными значениями падений напряжения, можно построить треугольник сопротивлений (рис. 20) Графически полное сопротивление будет представлять собой гипотенузу прямоугольного треугольника. Один катет такого треугольника равен R – его называют активным сопротивлением. Другой катет равен (w·L –  ), эту составляющую полного сопротивления называют реактивным сопротивлением и обычно обозначают X:
), эту составляющую полного сопротивления называют реактивным сопротивлением и обычно обозначают X:
X = XL – XC = w·L –  . .
| (28) |
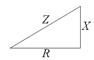
Рис. 20.
При условии w·L =  полное сопротивление цепи минимально и равно активному сопротивлению R0. Формула (26) показывает, что величина переменного тока в цепи существенно зависит от его частоты. При частоте w =
полное сопротивление цепи минимально и равно активному сопротивлению R0. Формула (26) показывает, что величина переменного тока в цепи существенно зависит от его частоты. При частоте w = 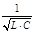 амплитудные значения тока принимают максимальные значения I0max = U0/R. Такое явление называют резонансом напряжений, а частоту w =
амплитудные значения тока принимают максимальные значения I0max = U0/R. Такое явление называют резонансом напряжений, а частоту w = 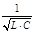 называют резонансной частотой электрической цепи. Величина тока при резонансе получается тем больше, чем меньше активное сопротивление цепи.
называют резонансной частотой электрической цепи. Величина тока при резонансе получается тем больше, чем меньше активное сопротивление цепи.
Параллельное соединение элементов
Рассмотрим цепь переменного тока, содержащую параллельно соединенные элементы R, L и C (рис. 21).

Рис. 21.
Пусть U(t) = U0·coswt. Напряжение на всех элементах цепи одинаково и равно U(t). Мгновенное значение тока в неразветвленной части цепи I(t) равно сумме токов в параллельных участках:
| I(t) = IR(t) + IC (t) + IL(t). | (29) |
В этом случае удобно строить векторную диаграмму для токов.
С учетом, что ток через сопротивление находится в фазе с приложенным напряжением, ток через участок, содержащий С, опережает напряжение на 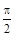 , а через участок, содержащий L, отстает от напряжения на
, а через участок, содержащий L, отстает от напряжения на 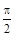 , векторную диаграмму можно изобразить следующим образом (рис. 22).
, векторную диаграмму можно изобразить следующим образом (рис. 22).
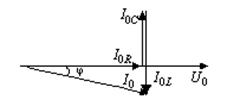
Рис. 22.
Из диаграммы видно, что
I0 =  . .
| (30) |
При этом
I0R·R =  = I0L·w·L = U0. = I0L·w·L = U0.
| (31) |
Воспользовавшись векторной диаграммой и формулой (31), нетрудно получить выражения для амплитуды тока через неразветвленную часть цепи и для сдвига по фазе между приложенным напряжением и током
 , ,
| (32) |
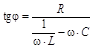 . .
| (33) |
Из векторной диаграммы следуют и выражения для мгновенных значений тока в ветвях цепи
IR =  , ,
| (34) |
IL = 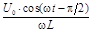 , ,
| (35) |
IC = U0·w·C·cos(wt + 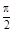 ). ).
| (36) |
При условии, что w·L =  , сдвиг фаз между током в неразветвленной части цепи и напряжением равен нулю (j = 0). При этом токи IL и IC находятся в противофазе и численно равны. Эти токи могут превосходить ток в подводящих проводах, что требует особенно внимательного соблюдения правил техники безопасности. Такая ситуация называется резонансом токов. При этом происходит периодический обмен энергией между электрическими и магнитными полями в емкости и индуктивности, а источник питания только компенсирует потери энергии на нагревание сопротивления R.
, сдвиг фаз между током в неразветвленной части цепи и напряжением равен нулю (j = 0). При этом токи IL и IC находятся в противофазе и численно равны. Эти токи могут превосходить ток в подводящих проводах, что требует особенно внимательного соблюдения правил техники безопасности. Такая ситуация называется резонансом токов. При этом происходит периодический обмен энергией между электрическими и магнитными полями в емкости и индуктивности, а источник питания только компенсирует потери энергии на нагревание сопротивления R.
Резонанс токов в цепи с параллельным соединением элементов приводит к тому, что ток во внешней цепи имеет наименьшее значение.
Если убрать сопротивление R, то ток в подводящих проводах будет равен нулю, хотя в контуре, состоящем из L и C, ток может быть очень большим. Это устройство используется в резонансных усилителях, в которых колебательный контур настраивается на частоту сигнала, который требуется усилить.
МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА
Напомним, что мощностью называется физическая величина, численно равная работе в единицу времени. Элементарная работа dA по переносу заряда dq, совершенная за время dt на участке цепи с падением напряжения U, определяется выражением
dA = U·dq.
Тогда мгновенная мощность:
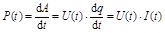 , ,
| (37) |
где U(t) и I(t) – мгновенные значения напряжения и силы тока.
В цепях синусоидального переменного тока, содержащих активное сопротивление R, индуктивность L и емкость C, ток, в общем случае, сдвинут по фазе относительно напряжения на угол φ:
U(t) = U0·cosωt,
I(t) = I0·cos(ωt + φ),
где U0 и I0 – амплитудные значения напряжения и силы тока, ω – круговая частота. Тогда элементарная работа dA за время dt:
| dA = U(t)·I(t)·dt = I0·U0·cosωt·cos(ωt + φ)·dt. | (38) |
Мгновенная мощность переменного тока также является величиной переменной. Для оценки энергетических свойств электроустановок используется значение средней мощности.
Для определения средней мощности P достаточно подсчитать работу тока за один период колебания T:

| (39) |
Воспользуемся формулой произведения косинусов:
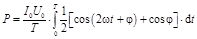 . .
| (40) |
Интеграл от первого слагаемого в квадратных скобках есть среднее значение косинуса за период и, следовательно, обращается в ноль. Таким образом, получили
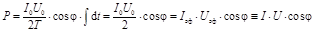 . .
| (41) |
Величину P = I·U·cosφ называют активной мощностью или средней мощностью, или просто мощностью переменного тока. Активная мощность в системе СИ измеряется в ваттах (1 Вт = 1 В ´ 1 А). Прибор, предназначенный для регистрации активной мощности, называется ваттметром (подробнее об устройстве и принципе действия ваттметра см. раздел «Ваттметр» в главе «Электроизмерительные приборы»).
Кроме активной мощности в теории переменных токов рассматривают полную(кажущуюся) мощность S = I·U иреактивную мощность Q = I·U·sinj.
Для того чтобы понять смысл реактивной мощности, рассмотрим энергетические процессы в цепи переменного тока, содержащей индуктивность L. В такой цепи потребление мощности в каждый момент времени не сводится только к выделению тепла. В той части периода, где ток нарастает, в катушке индуктивности L возбуждается магнитное поле, на что расходуется энергия источника. Когда же ток начинает уменьшаться, энергия, запасенная магнитным полем катушки, возвращается обратно источнику. Таким образом, индуктивность является то потребителем, то генератором энергии, а в среднем за период расход энергии в индуктивности равен нулю.
Аналогичные колебания происходят в цепи переменного тока, содержащей емкость C. В этом случае энергия запасается в электрическом поле конденсатора. Реактивная мощность Q не совершает никакой полезной работы, однако, она оказывает существенное влияние на режим функционирования электрических цепей. Поэтому расчет проводов и других элементов цепей переменного тока производят, исходя из полной мощности, которая учитывает активную и реактивную составляющие.
Очевидно, что активная P, реактивная Q и полная S мощности имеют одинаковую размерность. Однако в электротехнике, в отличие от единиц активной мощности, для удобства полную мощность принято измерять в вольт-амперах (ВА), а единица измерения реактивной мощности Q – вольт-ампер реактивный (ВАр).
Каким образом величины P, S и Q связаны между собой?
Для наглядности рассмотрим векторную диаграмму напряжений для последовательной цепи переменного тока, содержащей R, L и C, изображенную на рис. 23.

| ||
| а | б | в |
Рис. 23.
Сумма коллинеарных векторов UL и UC и перпендикулярного им вектора UR равна вектору U, который отображает общее падение напряжения в цепи. Он сдвинут относительно вектора тока I на угол j. Вектора U, UR и (UL + UC) образуют треугольник напряжений А0В (прямоугольный), причем катет АВ численно характеризует падение напряжения на чисто реактивной, а 0В – на чисто активной нагрузках:
| АВ = U·sinj, 0В = U·cosj. | (42) |
Разделив стороны векторного треугольника напряжений на величину силы тока I, получаем треугольник сопротивлений A′0′B′ (рис. 23,б), который уже не будет векторным. Умножив стороны треугольника напряжений на I, получаем треугольник мощностей A″0″B″, также не векторный (рис. 23,в). Очевидно, что эти три треугольника подобны. Сопоставляя стороны треугольника мощностей и треугольника напряжений, заключаем:
| 0″A″ = I·U = S ← полная мощность, | (43) |
| 0″B″ = I·U·cosj = S·cosj = P ← активная мощность, | (44) |
| А″B″ = I·U·sinj = S·sinj = Q ← реактивная мощность. | (45) |
И, как видно из треугольника A″0″B″, справедливо соотношение:
| S2 = P2 + Q2. | (46) |
То есть полная мощность является геометрической суммой активной и реактивной мощностей.
Стороны треугольника сопротивлений и треугольника мощностей по построению связаны следующим образом:
| P = I2·R, | (47) |
| Q = I2·(XL – XC) = I2·X, | (48) |
| S = I2·Z, | (49) |
где R – активное сопротивление цепи, X – реактивное сопротивление, XL = wL – индуктивное сопротивление, XC = 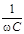 – емкостное сопротивление,
– емкостное сопротивление, 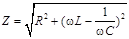 – полное сопротивление (импеданс) цепи переменного тока.
– полное сопротивление (импеданс) цепи переменного тока.
Если известны индуктивная QLi и емкостная QCi составляющие реактивной мощности и активная Pi мощность каждого i-го потребителя, то полная мощность, на которую должен рассчитываться источник, составляет
 . .
| (50) |
Величина cosj, стоящая в выражении для активной мощности (см. формулу (44)), показывает, какая часть полной мощности цепи приходится на долю активной мощности, поэтому cosj называют коэффициентом мощности.
Из формулы (50) видно, что коэффициент мощности можно увеличить, уменьшая второе слагаемое под корнем. Большинство промышленных потребителей (трансформаторы, электродвигатели) потребляют индуктивную реактивную мощность. Для уменьшения такой реактивной мощности параллельно индуктивной нагрузке включают емкость.
[1] Подробнее о целесообразности введения эффективных значений тока и напряжения см. в разделе «Мощность переменного тока».
1 При построении векторной диаграммы можно вместо амплитудных значений использовать эффективные (см. предыдущий раздел).
[2] Подробнее см. в разделе «Приложения. Построение векторных диаграмм».
| <== предыдущая лекция | | | следующая лекция ==> |
| ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЛИНЕЙНОГО И ОБЪЕМНОГО РАСШИРЕНИЯ ПОЛИКРИСТАЛЛИЧЕСКИХ ТЕЛ ПРИ НАГРЕВАНИИ | | | Предмет і задачі фізіології. Методи фізіологічних досліджень. |
Дата добавления: 2016-04-19; просмотров: 3919;
