Раздвижение пластин конденсатора
Задача 4.2. Изолированный воздушный конденсатор заряжен зарядом Q, площадь его пластин S, а расстояние между пластинами d1. Какую работу необходимо совершить внешней силой, чтобы увеличить расстояние между пластинами до величины d2 > d1?
| Q S d1 d2 d2 > d1 | Решение. Работа внешней силы пойдет на увеличение энергии конденсатора, поэтому
А = W2 – W1 = 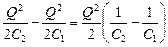 = =
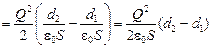 . .
|
| А = ? | |
Ответ: А 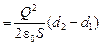 .
.
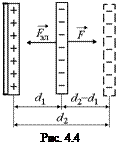 Читатель: А нельзя ли вычислить работу непосредственно по формуле А = Fэл(d2 – d1), где Fэл – сила, с которой притягиваются пластины?
Читатель: А нельзя ли вычислить работу непосредственно по формуле А = Fэл(d2 – d1), где Fэл – сила, с которой притягиваются пластины?
Автор: Можно. Ведь чтобы раздвинуть пластины, одну из них надо закрепить, а к другой приложить силу, равную той, с которой притягиваются пластины, и переместить незакрепленную пластину на расстояние (d2 – d1) (рис. 4.4). Сила F с которой притягиваются пластины, равна
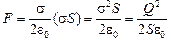 .
.
Тогда
А = F(d2 – d1) = 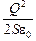 (d2 – d1).
(d2 – d1).
Как видим, мы получили тот же результат.
СТОП! Решите самостоятельно: А6, В3–В5.
Задача 4.3. Плоский воздушный конденсатор подключили к источнику постоянного напряжения величины U. Площадь пластин конденсатора S, расстояние между ними d1. Какую работу необходимо совершить внешней силой, чтобы уменьшить расстояние между пластинами до величины d2 < d1?
| Q S d1, d2 d2 < d1 | Решение. Читатель: Так как пластины притягиваются друг к другу, то, по-моему, никакой работы внешней силе вообще совершать не надо. Нужно только не мешать пластинам двигаться навстречу друг другу. | |
| Авнеш = ? | ||
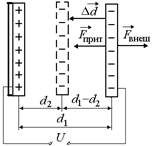 Рис. 4.5
Рис. 4.5
| Автор: Вы правы, но если мы не хотим, чтобы пластины при этом разгонялись и приобретали кинетическую энергию, надо закрепить одну из пластин, а другую притормаживать внешней силой так, чтобы она двигалась с постоянной скоростью: 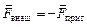 (рис. 4.5).
Читатель: Тогда работа внешней силы будет отрицательной, так как (рис. 4.5).
Читатель: Тогда работа внешней силы будет отрицательной, так как 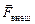 и и
| |
вектор перемещения 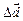 (
( 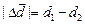 ) составят угол 180° (см. рис. 4.5).
) составят угол 180° (см. рис. 4.5).
Автор: И как же нам найти работу внешней силы?
Читатель: Она равна изменению энергии конденсатора:
Авнеш = W2 – W1 = 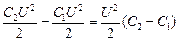 =
=
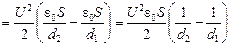 .
.
Автор: Но d2 < d1, значит, 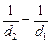 > 0, т.е. Авнеш > 0! А Вы только что доказали, что Авнеш < 0. В чем же дело?
> 0, т.е. Авнеш > 0! А Вы только что доказали, что Авнеш < 0. В чем же дело?
Читатель: Не понимаю.
Автор: Вспомним, что наш конденсатор подключен к источнику напряжения, и в процессе сближения пластин напряжение поддерживается постоянным, а вот емкость в процессе сближения пластин увеличивается: С2 > С1. Следовательно, заряд на пластинах также увеличивается:
 Q2 = C2U > Q1 = C1U.
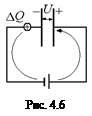
Q2 = C2U > Q1 = C1U.
Таким образом, источник напряжения как бы «перетащил» заряд DQ = Q2 – Q1 = (C2 – C1)U с отрицательно заряженной пластины на положительно заряженную (рис. 4.6). При этом источнику пришлось совершить работу против сил электрического поля в конденсаторе:
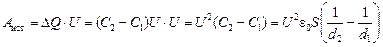 .
.
А общая работа источника напряжения и внешней силы как раз равна изменению энергии конденсатора:
Аист + Авнеш = W2 – W1.
Тогда
Авнеш = (W2 – W1) – Аист = = 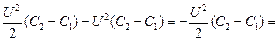
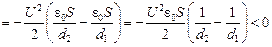 .
.
Как видите, работа внешних сил действительно получилась отрицательной.
Ответ: 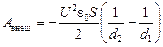 .
.
Читатель: Если пластины раздвигать, то работа внешних сил, конечно, будет положительной, а вот какой будет работа источника?
Автор: Отрицательной. Ведь заряды на пластинах будут уменьшаться, следовательно, DQ = Q2 – Q1 < 0 и Аист = DQU < 0. То есть конденсатор, разряжаясь, будет передавать свою энергию источнику напряжения (аккумулятору), заряжая его.
СТОП! Решите самостоятельно: В6, С4–С6.
Задача 4.4. Изолированный конденсатор имеет заряд Q. Между его обкладками находится пластина из диэлектрика с диэлектрической проницаемостью e. Емкость конденсатора без пластины равна С. Какую работу надо совершить внешней силой, чтобы вытащить пластину из конденсатора?
| Q С e | Решение. Читатель: Я не понимаю, почему для того, чтобы вытащить пластину диэлектрика из конденсатора, надо совершать работу. Ведь поле в конденсаторе однородно, значит, никаких сил, действующих по касательным к пластинам, быть не может. Кроме того, пластина из диэлектрика электрически нейтральна. Автор: Во-первых, на краях обкладок поле неоднородно, а во-вторых, не надо забывать про поляризационные заряды! Силовые линии на краях конденсатора имеют вид, показанный на рис. 4.7. Мы видим, что |
| Авнеш = ? | |
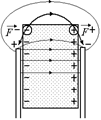 Рис. 4.7
Рис. 4.7
|
напряженность поля там как раз имеет касательную к пластинам составляющую. И именно из-за этого на поляризационные заряды действует сила, «возвращающая» пластину в конденсатор. Поэтому чтобы вытащить пластину из конденсатора, необходимо приложить внешнюю силу.
Теперь осталось вычислить работу внешней силы. Если емкость конденсатора без диэлектрика равна C0, то емкость с диэлектриком eС0. Тогда начальная энергия конденсатора 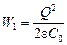 , а конечная
, а конечная 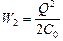 . Работа внешней силы равна изменению энергии конденсатора:
. Работа внешней силы равна изменению энергии конденсатора:
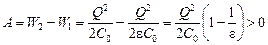 .
.
Ответ: 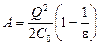 .
.
СТОП! Решите самостоятельно: А7, В7–В9, С7.
Задача 4.5. Воздушный конденсатор емкостью С0 подключен к источнику напряжения U. Какую работу надо совершить внешней силе, чтобы вставить в конденсатор пластину из диэлектрика с диэлектрической проницаемостью e?
| U C0 e | Решение. Сначала заряд на конденсаторе был равен Q1 = C0U. После того как вставили пластину, заряд увеличился и стал равным Q1 = eC0U. Следовательно, источник совершил работу Аист = U(Q2 – Q1) = U(eC0U – C0U) = U2C0(e – 1) > 0. |
| Авнеш = ? | |
Суммарная работа источника и внешней силы равна изменению энергии конденсатора:
Аист + Авнеш = W2 – W1.
Тогда
Авнеш = (W2 – W1) – Аист = 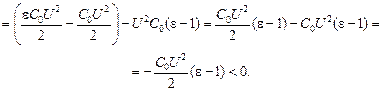
Таким образом, работа внешней силы отрицательна: пластина сама будет втягиваться в конденсатор.
Ответ: Авнеш 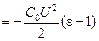 .
.
СТОП! Решите самостоятельно: В11, В12, В14.
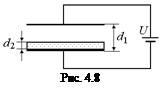 Задача 4.6. Плоский конденсатор подключен к источнику напряжения U (рис. 4.8). Площадь каждой пластины конденсатора S, расстояние между пластинами d1. К нижней пластине прижата металлическая пластинка той же площади S, толщины d2 и массы т. Металлическую пластинку отпускают. С какой скоростью она ударится о верхнюю пластину конденсатора? Силой тяжести пренебречь.
Задача 4.6. Плоский конденсатор подключен к источнику напряжения U (рис. 4.8). Площадь каждой пластины конденсатора S, расстояние между пластинами d1. К нижней пластине прижата металлическая пластинка той же площади S, толщины d2 и массы т. Металлическую пластинку отпускают. С какой скоростью она ударится о верхнюю пластину конденсатора? Силой тяжести пренебречь.
| U S d1 d2 m | Решение. Если бы конденсатор не был подключен к источнику напряжения, то после того, как пластинка «подпрыгнула» и ударилась о верхнюю обкладку, конденсатор бы полностью разрядился. Однако в данном случае источник «загонит» на обкладку новые заряды +q и –q в точности равные старым: q = CU. При этом |
| υ = ? |
энергия конденсатора 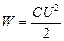 не изменится, но источник совершит работу
не изменится, но источник совершит работу 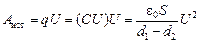 .
.
И эта работа как раз и пойдет на увеличение кинетической энергии пластинки: 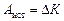 , тогда
, тогда
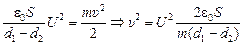 .
.
Ответ: 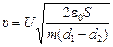 .
.
СТОП! Решите самостоятельно: С11–С13.
Дата добавления: 2016-04-11; просмотров: 11706;
