Задачи средней трудности. В1. Площадь каждой пластины плоского конденса­тора S = 200 см2, а расстояние между ними d = 1,00 см

В1. Площадь каждой пластины плоского конденса­тора S = 200 см², а расстояние между ними d = 1,00 см. Какова энергия поля, если напряженность поля Е = 500 кВ/м?

В2. Как изменится энергия конденсатора, если при той же разности потенциалов между пластинами увеличить все его геометрические размеры в k раз? При тех же размерах увеличить заряд в п раз?

В3. Определить работу, которую необходимо совершить, чтобы увеличить расстояние между пластинами плоского воздуш­ного конденсатора на l = 0,400 мм. Площадь каждой пластины равна S = 2p×10⁴ мм², заряд составляет q = 2,00×10^–7 Кл.

В4.Плоский воздушный конденсатор емкости С = 1,6×10³ пФ зарядили до разности потенциалов U = 500 В, отключили от источника напряжения и увеличили расстояние между пластинами в три раза. Определить разность потенциалов на пластинах конденсатора после их раздвижения и работу, совершенную внешними силами для раздвижения пластин.

В5. Пластины изолированного плоского конденсатора раздвигают так, что емкость его меняется от C₁до С₂(C₁ > С₂).Какую работу надо совершить при этом, если заряд конденсатора q? При решении учесть, что напряженность поля между пластинами равна сумме напряженностей полей от каждой из пластин в отдельности.

В6. Конденсатор подключен к аккумулятору. Раздвигая пластины конденсатора, мы преодолеваем силы притяжения между пластинами конденсатора и, следовательно, совершаем работу. На что затрачивается эта работа? Что происходит с энергией конденсатора?

В7.Плоский воздушный конденсатор с площадью пластин S = 80 см² каждая и расстоянием между ними d = 1,5 мм заряжается от источника с напряжением U = 100 В, отключается от него и погружается в жидкий диэлектрик с относительной диэлектрической проницаемостью e = 2,5. Как и на сколько изменится при этом энергия конденсатора?

В8.Между обкладками плоского конденсатора находится пластина из диэлектрика. Емкость конденсатора равна С, его заряд равен Q, диэлектрическая проницаемость материала пластинки равна e. Какую работу надо совершить, чтобы вытащить пластинку из конденсатора? (Трение между пластинкой и обкладками конденсатора не учитывать.)

В9. Между обкладками плоского конденсатора находится парафиновая пластинка. Емкость конденсатора С = 4,0 мкФ, его заряд q = 0,20 мКл. Какую работу нужно совершить, чтобы вытащить пластинку из конденсатора?

В10. Конденсатор емкости С без диэлектрика имеет заряд q. Какое количество теплоты выделится в конденсаторе, если его заполнить веществом с диэлектрической проницаемостью e?

В11. К батарее с напряжением U = 200 В подключили воздушный конденсатор, площадь пластин которого S = 12,6 см², а рас­стояние между пластинами d = 1 мм. Какую работу совершит батарея при заполнении пространства между обкладками конден­сатора диэлектриком, диэлектрическая проницаемость которого e = 5,5? Как при этом изменится запасенная в конденсато­ре энергия?

В12. Конденсатор емкости С подключен к батарее. Какое количество теплоты выделится в конденсаторе, если его заполнить веществом с диэлектрической проницаемостью e? Батарея поддерживает на конденсаторе постоянную разность потенциалов V.

В13. Энергия плоского воздушного конденсатора W₁= 2×10^–7 Дж. Опре­делить энергию конденсатора после заполнения его диэлектриком с диэлектри­ческой проницаемостью e= 2, если конденсатор:

1) отключен от источника питания;

2) подключен к источнику питания.

В14.Плоский конденсатор с диэлектриком (e = 4,0) приобрел энергию W = 0,12 Дж от подключенного к нему источника напряжения. Определить работу внешних сил А по удалению диэлектрика из пространства между пластинами и работу источника А₀.

В15. Плоский конденсатор имеет пластины площадью S, расположенные на расстоянии d. Пластины заряжены с поверхностной плотностью заряда +s и –s. Между пластинами находится диэлектрик с диэлектрической проницаемостью e. Найти работу, которую необходимо совершить внешней силе для увеличения расстояния между пластинами в 3 раза.

Задачи трудные

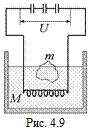С1.Батарею конденсаторов ёмкостью С = 4 мкФ, заряженную до напряжения U = 30 кВ, разряжают через спираль с большим сопротивлением, помещенную в калориметр с водой (М = 90 г) и льдом (т = 10 г) при t₀ = 0 °С. Определить состав и температуру смеси в калориметре после разрядки батареи. Удельная теплота плавления льда l = 0,34×10⁶ Дж/кг, удельная теплоёмкость воды с₀ = 4,2 кДж/кг×К (рис. 4.9).

С2. Напряженность поля в конденсаторе Е, диэлектрическая проницаемость диэлектрика e, площадь пластин S, начальное расстояние между пластинами d. Какая энергия выделится в конденсаторе, если расстояние между его пластинами увеличить в 2 раза?

С3. Расстояние между пластинами плоского воздуш­ного конденсатора, присоединенного к источнику напряжения U = 180 В равно d₁ = = 5,0 мм. Площадь пластин конденсатора S = 175 см². Найти работу по раздвижению пластин до расстояния d₂ = 12 мм в двух случаях: 1) конденсатор перед раздвижением пластин отключен от источника; 2) конденсатор в процессе раздвижения пластин все время соединен с источником.

С4.Расстояние между пластинами плоского воздушно­го конденсатора, присоединенного к источнику напряжения U,равно d₁,площадь пластин S. Найти работу по раздвижению пластин конденсатора до расстояния d₂ > d_l,если конденсатор в процессе раздвижения пластин соединен с источником напря­жения.

С5.Максимальная емкость, конденсатора настройки в радиоприемнике равна С₁ = 100 пФ. Путем поворота подвижных пластин емкость конденсатора может быть уменьшена до С₂ = 10 пФ.Предположим, что кон­денсатор заряжен до разности потенциалов U = 300 В,когда его емкость максимальна. Затем ручку на­стройки поворачивают, и емкость конденсатора становится минимальной. Чему равна работа внешней силы, совершенная при повороте ручки настройки?

С6.Расстояние между пластинами заряженного плоского конденсатора увеличивают в п раз. Как при этом изменяется запасенная в конденсаторе энергия? Рассмотреть случаи, когда конденсатор: а) подключен к источнику постоянного напряжения; б) отключен от источника.

С7.Плоский воздушный конденсатор заполнили керосином (e =2) и зарядили, сообщив ему энергию W. Затемконденсатор отсоединили от источника, слили керо­син иразрядили. Какая энергия выделилась при разряде?

С8. Плоский конденсатор с площадью пластин S имеет заряд q. Докажитечто при раздвижении пластин на расстояние х нужно совершить работу, равную объему пространства, которое заполнит вновь созданное электрическое поле напряженности Е, умноженному на плотность энергии e₀Е²/2.

С9.Одна из пластин плоского конденсатора емкости С имеет за­ряд +q,а другая +5q. Какая энергия запасена в таком кон­денсаторе? Какие заряды следует поместить на обкладки, чтобы при той же энергии в конденсаторе электрическое поле вне его не существовало?

C10.Большая тонкая проводящая пластина площади S и толщины d помещена в однородное электрическое поле напряженности Е перпендикулярно пла­стине. Какое количество теплоты выделится в проводнике, если поле мгновенно выключить?

С11. Конденсатор емкостью С = 1,0 мФ при напряжении U = 1200 В применяют для импульсной стыковой сварки медной проволоки. Найти среднюю полезную мощность разряда, если он длится 1,0×10^–6 с. КПД установки 4%.

С12. Плоский конденсатор находится во внешнем однород­ном электрическом поле напряженности Е, направление которого совпадает с направлением поля в конденсаторе. По пластинам, площадь которых равна S, равномерно рас­пределены заряды q и –q. Какую работу нужно совершить, чтобы перевернуть конденсатор, поменяв пластины местами? Расстояние между пластинами равно d. Влиянием силы тяжести пренебречь.

С13.Верхняя пластина плоского конденсатора площадью S ви­сит на пружине, жесткость которой k. Какую разность потенциалов нужно приложить к пластинам конденсатора, чтобы они сблизились до расстояния d₁?Начальное расстояние между пластинами равно d₀.

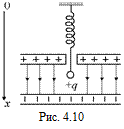
С14.К нерастянутой вертикальной пружине, концы которой сначала закреплены, подвешивают шарик мас­сой т, имеющий положительный заряд q. Шарик нахо­дится в однородном электростатическом поле плоского конденсатора (рис. 4.10) с напряженностью Е. Затем ко­нец пружины освобож­дают. Найдите новое положение равновесия шарика и подсчитайте изменение энергии при переходе в это состоя­ние. Объясните резуль­тат.