Схема сложных процентов.

1. Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Пусть исходный инвестируемый капитал равен Р, требуемая доходность - r(в долях единицы). Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину Р*r. Таким образом, размер инвести­рованного капитала (Rn) через п лет будет равен:

R_n = P + P*r + … + P*r = P (1 + n*r).

2. Считается, что инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходной величины инве­стированного капитала, а с общей суммы, включающей также и ранее на­численные и не востребованные инвестором проценты. В этом случае происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляются проценты, все время возрастает. Следовательно, размер инвестированного капитала будет равен:

к концу 1-го года: F₁= Р + Р*r = Р(1+r);

к концу 2-го года: F₂ = F₁ + F₁ *r = F₁(1 +r) = Р(1 + r)²;

…

к концу n-го года: F_п= Р • (1+г)ⁿ.

В случае краткосрочных ссуд со сроком погашения до одного года в качестве показателя п берется величина, характеризующая удельный вес длины подпериода (дни, месяц, квартал, полугодие) в общем периоде (год). Длина различных временных интервалов в расчетах может округ­ляться: месяц - 30 дней; квартал - 90 дней; полугодие - 180 дней; год -360 (или 365, 366) дней.

2. Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности.

На практике многие финансовые операции выполняются в рамках од­ного года, при этом могут использоваться различные схемы и методы на­числения процентов. В частности, большое распространение имеют краткосрочные ссуды, т.е. ссуды, предоставляемые на срок до одного года с однократным начислением процентов. Как отмечалось выше, в этом случае для кредитора, диктующего чаще всего условия финансового контракта, более выгодна схема простых процентов, при этом в расчетах используют промежуточную процентную ставку, которая равна доле го­довой ставки, пропорциональной доле временного интервала в году.

F = P * (1 + f*r) или F = P * (1 + t/T*r),

где r - годовая процентная ставка в долях единицы;

t - продолжительность финансовой операции в днях;

Т- количество дней в году;

f- относительная длина периода до погашения ссуды.

Для наглядности формулу можно записать следующим обра­зом:

F = P * (1 + t*r/T),

т.е. дробь r/Т представляет собой дневную ставку, а произведение t*r/T -ставку за t дней.

Определяя продолжительность финансовой операции, принято день выдачи и день погашения ссуды считать за один день.

В практике финансовых операций нередко оговаривается не только величина годового процента, но и количество периодов начисления процентов. В этом случае расчет ведется по формуле сложных процентов по подынтервалам и по ставке, равной пропорциональной доле исходной годовой ставки, по формуле:

F_n = P*(1 + r/m)^n*m,

где r- объявленная годовая ставка;

т - количество начислений в году;

п - количество лет.

Модели инфляции

Инфляция характеризуется обесценением национальной валюты, снижением ее покупательной способности и общим повышением цен в стране. В таком случае инвестор может потерять часть дохода, а заемщик соответственно может выиграть за счет погашения задолженности деньгами сниженной покупательной способности. На этом основании необходимо установить количественные соотношения по определению влияния инфляции на показатели финансовой операции. Следует заметить, что если наблюдается общее снижение цен, то происходит дефляция.

Все показатели финансовой операции можно разделить на две группы: номинальные, рассчитанные в текущих ценах, и реальные, учитывающие влияние инфляции, рассчитанные в сопоставимых ценах базисного периода.

Для количественной оценки упомянутых процессов формируют определенный набор товаров и услуг, называемый потребительской корзиной, и фиксируют изменение ее стоимости в различные моменты времени. Состав потребительской корзины математически можно представить в виде n-мерного вектора:

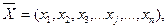
где х- количество i-го вида товара или услуги в корзине:

п - количество товаров и услуг потребительской корзины.

В базисном периоде /о цены состава потребительской корзины можно представить в виде n-мерного вектора

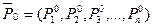
а в анализируемом периоде t_j соответственно вектором

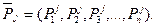
Тогда стоимость потребительской корзины описывается скалярным произведением векторов 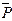и .

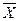S= .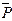

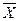Стоимость корзины в базисном периоде t₀ составит:

,

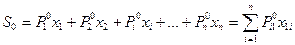а в анализируемом периоде t_j составит:

,

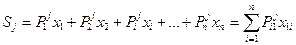На этом основании полагают, что изменение (рост или падение) потребительских цен определяется безразмерным показателем, называемым индексом инфляции, который показывает, во сколько раз выросли цены;

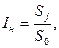
а относительная величина уровня инфляции есть темп инфляции:

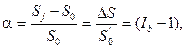
откуда следует, что индекс инфляции равен: I_и = 1 + α.

Уровень инфляции в процентах определяется так:

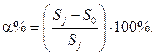
Индекс инфляции показывает, во сколько раз выросли цены, а уровень инфляции - на сколько процентов выросли цены за рассматриваемый период.

Рассмотрим различные варианты начисления процентов с учетом инфляции.

Для простых процентов обозначим i_α ставку процентов, учитывающую инфляцию, тогда наращенную сумму можно определить по формуле

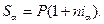
Затем, воспользовавшись уравнением связи S_α с S с помощью индекса инфляции:

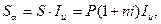
запишем равенство

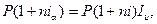
откуда и получим модель определения ставки процентов, учитывающую инфляцию,

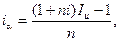
Реальная доходность операции при заданных 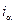и 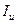определяется по формуле

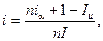
Для сложных процентов аналогично запишем два выражения:

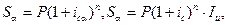
из которых определим:

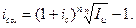
Эту формулу можно записать так:

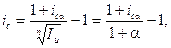
по которой можно сравнивать 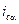и α (больше, равно или меньше), проводить экономический анализ эффективности вложений и установить, поглощается ли доход инфляцией или про реальный прирост вложенного капитала, а не убыток.