Мультипликативная модель.

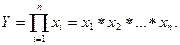
Пример 2. Выручка от реализации продукции (объем продукции - V) может быть выражена как произведение комплекса факторов: численность персонала (Чп), доля рабочих в общей численности персонала (dр); среднегодовая выработка одного рабочего (Вр)

V = Чп * dр * Вр

Кратная модель.

Пример 3. Рентабельность продукции (Рпр) представляет собой частное от деления прибыли от реализации (Преал.) на выручку от реализации (Vр.п):

Преал Рпр = ¾¾¾ * 100 . Vр.п

a + b a a * b Y = ¾¾¾ ; Y = ¾¾¾ ; Y = ¾¾¾ ; Y = (a + b) * c и т.д. c b + c c

Смешанная (комбинированная) модель представляет собой сочетание в различных комбинациях предыдущих моделей:

Пбал Р = ¾¾¾ . ОС + ОБ

Пример 4. Рентабельность предприятия (Р) определяется как частное от деления балансовой прибыли (Пбал) на среднегодовую стоимость основных (ОС) и нормируемых оборотных (ОБ) средств:

Ø Преобразования детерминированных факторных моделей

Для моделирования различных ситуаций в факторном анализе применяются специальные методы преобразования типовых факторных моделей. Все они основаны на приеме детализации. Детализация – разложение более общих факторов на менее общие. Детализация позволяет на основе знания экономической теории упорядочить анализ, содействует комплексному рассмотрению факторов, указывает значимость каждого из них.

Развитие детерминированной факторной системы достигается, как правило, за счет детализации комплексных факторов. Элементные (простые) факторы не раскладываются.

Пример 1. Факторы

Vрп = Чп * Вп = = Чп * dр * Вр = = Чп * dр * Дн * Вдн = = Чп * dр * Дн * РДчас * Вчас

1-го порядка 2-го порядка 3-го порядка 4-го порядка

Условные обозначения: Vрп– объем реализованной продукции; Чп – численность персонала; Вп – средняя годовая выработка персонала; dр – доля рабочих в общей численности персонала; Вр – среднегодовая выработка одного рабочего; Дн – среднее число дней отработанных в течение года 1 рабочим; Вдн – средняя дневная выработка; РДчас– средняя продолжительность рабочего дня; Вчас – средняя годовая выработка

Большая часть традиционных (специальных) приемов детерминированного факторного анализа основана на элиминировании. Прием элиминирования используется для определения изолированного фактора путем исключения воздействия всех остальных. Исходной посылкой данного приема является следующая: Все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, затем изменяются два, три и т.д. при неизменности остальных. Прием элиминирования является в свою очередь основой для других приемов детерминированного факторного анализа, цепных подстановок, индексных, абсолютных и относительных (процентных) разниц.

Ø Прием цепных подстановок

Цель. Измерение изолированного влияния факторов на изменение результативного показателя.

Область применения. Все виды детерминированных факторных моделей.

Ограничение на использование. Факторы в модели должны быть последовательно расположены: от количественных к качественным, от более общих к более частным.

Порядок применения. Рассчитывается ряд скорректированных значений результативного показателя путем последовательной замены базисных значений факторов на фактические.

Расчет влияния факторов целесообразно проводить в аналитической таблице.

Исходная модель: П = А х В х С х Д

Постановки

Факторы

Результатив-ный показатель, П

Изменение результативного показателя, _DП

Причина отклонения

А_о А₁ А₁ А₁ А₁

В₀

В₁

С₀ С₀ С₀ С₁ С₁

Д₀ Д₀ Д₀ Д₀ Д₁

П₀ П^/ П^// П^/ П₁

_DП^А=П^/-П_о _DП^в=П^//-П^/ _DП^с=П^///-П^// _DП^д=П₁-П^///

изменение фактора А изменение фактора В изменение фактора С изменение фактора Д

Баланс отклонений: D П = D П^а + D П^в + D П^с+ D П^д

Ø Прием абсолютных разниц

Цель. Измерение изолированного влияния факторов на изменение результативного показателя.

Область применения.Детерминированные факторные модели; в том числе:

1. Мультипликативные

2. Смешанные (комбинированные)

типа Y = (A-B)C и Y = A(B-C)

Ограничения на использование. Факторы в модели должны быть последовательно расположены: от количественных к качественным, от более общих к более частным.

Порядок применения.Величина влияния отдельного фактора на изменение результативного показателя определяется путем умножения абсолютного прироста исследуемого фактора на базисную (плановую) величину факторов, которые в модели находятся справа от него, и на фактическую величину факторов, расположенных слева.

В случае исходной мультипликативной модели П = А х В х С х Д получим: изменение результативного показателя

1. За счет фактора А:

DП^А = (А₁ – А₀) х В₀ х С₀ х Д₀

2. За счет фактора В:

DП^В = А₁х (В_{1 -}В₀) х С₀ х Д₀

3. За счет фактора С:

DП^С = А₁ х В₁ х (С₁ - С₀) х Д₀

4. За счет фактора Д:

DП^Д = А₁ х В₁ х С₁ х ( Д₁- Д₀)

5. Общее изменение (отклонение) результативного показателя (баланс отклонений)

D П = D П^а + D П^в + D П^с+ D П^д

Баланс отклонений должен соблюдаться (так же как в приеме цепных подстановок).

Ø Прием относительных (процентных) разниц

Цель. Измерение изолированного влияния факторов на изменение результативного показателя.

Область применения. Детерминированные факторные модели, включая:

1) мультипликативные;

2) комбинированные типа Y = (А – В) С,

целесообразно применять, когда известны определенные ранее относительные отклонения факторных показателей в процентах или коэффициентах.

Требования к последовательности расположения факторов в модели отсутствуют.

Исходная посылка. Результативный признак изменяется пропорционально изменению факторного признака.

Порядок применения. Величина влияния отдельного фактора на изменение результативного показателя определяется путем умножения базисного (планового)значения результативного показателя на относительный прирост факторного признака.

Исходная модель:

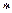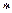Y = А В С

Изменение результативного показателя:

1. За счет фактора А:

Y₀ x DА% А₁ – А₀ DY^А = ¾¾¾¾¾, где DА% = ¾¾¾¾ х 100 ₁₀₀А₀

( Y₀ + DY^А )x DВ% В₁ – В₀ DY^В = ¾¾¾¾, где DВ% = ¾¾¾¾ х 100 ₁₀₀В₀

За счет фактора В:

2. За счет фактора С:

(Y₀ + DY^А + DY^В )x DС% С₁ – С₀ DY^С = ¾¾¾¾¾, где DС% = ¾¾¾¾ х 100 100 С₀

Баланс отклонений. Общее отклонение результативного показателя складывается из отклонений по факторам:

D Y = Y₁- Y₀ = D Y^A + D Y^B+ D Y^C

Ø Индексный метод

Цель. Измерение относительного и абсолютного изменения экономических показателей и влияния на него различных факторов.

Область применения.

1. Анализ динамики показателей, в том числе агрегированных (сложенных).

2. Детерминированные факторные модели; включая мультипликативные и кратные.

Порядок применения. Абсолютное и относительное изменение экономических явлений.

Агрегатный индекс стоимости продукции (товарооборота)

åp₁ q₁ I pq = ¾¾¾¾. åp_o q₀

I pq – характеризует относительное изменение стоимости продукции в действующих ценах (ценах соответствующего периода)

Разность числителя и знаменателя (åp₁ q₁- åp_o q₀) – характеризует абсолютное изменение стоимости продукции в отчетном периоде по сравнению с базисным.

Агрегатный индекс цен:

åp₁ q₁ I p = ¾¾¾¾ åp_o q₁

I p – характеризует относительное изменение средней цены на совокупность видов продукции (товаров).

Разность числителя и знаменателя (åp₁ q₁- åp_o q₁) – характеризует абсолютное изменение стоимости продукции вследствие изменения цен на отдельные ее виды.

å q₁ p₀ I q = ¾¾¾¾ åq₀ p₀

Агрегатный индекс физического объема продукции:

характеризует относительное изменение объема продукции в фиксированных (сопоставимых) ценах.

åq₁ p₀- åq₀ p₀ – разность числителя и знаменателя характеризует абсолютное изменение стоимости продукции вследствие изменения физических объемов различных ее видов.

На основе индексных моделей проводится факторный анализ.

Так, классической аналитической задачей является определение влияния на стоимость продукции фактора количества (физического объема) и цен:

Ipq = Ip x Iq

В абсолютных величинах

å p₁ q₁- å p₀ q₀= (å q₁p₀- å q₀ p₀) + (å p₁ q₁- å p₀ q₁).

Аналогично, используя индексную модель, можно определить влияние на полную себестоимость продукции (zq) факторов ее физического объема (q) и себестоимости единицы продукции различных видов (z)

Izq = Iq x Iz

В абсолютном выражении

å z₁ q₁- å z₀ q₀= (å q₁z₀- å q₀ z₀) + (å z₁ q₁- å z₀ q₁)

Ø Интегральный метод

Цель. Измерение изолированного влияния факторов на изменение результативного показателя.

Область применения. Детерминированные факторные модели, в том числе

· Мультипликативные

· Кратные

· Смешанные типа

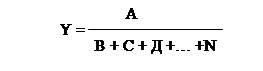
Преимущества. По сравнению с приемами, основанными на элиминировании, дает более точные результаты, поскольку дополнительный прирост результативного показателя за счет взаимодействия факторов распределяется пропорционально их изолированному воздействию на результативный показатель.

Порядок применения. Величина влияния отдельного фактора на изменение результативного показателя определяется на основе формул для разных факторных моделей, выведенных с применением дифференцирования и интегрирования в факторном анализе.

1. ¦= х ×у

Изменение результативного показателя за счет фактора х

D¦_х = D ху₀ +DхDу / 2

за счет фактора у

D¦_у = D ух₀ +DуDх / 2

Общее изменение результативного показателя: D¦ = D¦_х + D¦_у

Баланс отклонений

D¦ = ¦₁ - ¦₀ = D¦_х +D¦_у

<1 2 345 6 7 >

Дата добавления: 2016-04-11; просмотров: 5593;