Погруженный в жидкость

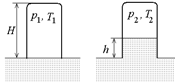
Задача 4.5. Цилиндрический сосуд высотой Н стоит вверх дном, едва касаясь поверхности жидкости плотностью r (рис. 4.3,а). Температура воздуха в сосуде Т₁. Через некоторое время жидкость поднялась в сосуде на высоту h (рис. 4.3,б). Какова была в этот момент температура воздуха в сосуде? Атмосферное давление р₀.

Н Т1 r р0 h	а б Рис. 4.3	Решение. Согласно формуле (4.1) 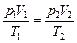. (1) Начальный объем V1 = HS, (2) где S – площадь дна сосуда.
Т2 = ?

Конечный объем

V₂ = (H – h)S. (3)

Начальное давление равно атмосферному

р₁ = р₀. (4)

Конечное давление меньше атмосферного на rgh:

р₂ = р₀ – rgh. (5)

Подставляя (2)–(5) в (1), получим:

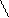
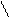
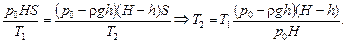
Ответ: .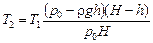

СТОП! Решите самостоятельно: С6, С7, С14.

Смежные объемы, разделенные

Подвижным поршнем

Задача 4.6. В горизонтально расположенном цилиндрическом сосуде находятся две массы газа, разделенные подвижным теплонепроницаемым поршнем при температурах Т₁ и Т₂ соответственно (Т₁ < Т₂). В начальный момент поршень делит сосуд пополам (рис. 4.4,а). Найти отношение объемов газа слева и справа от поршня после того, как левую и правую половины сосуда нагрели на DТ.

Т1 Т2 DТ	а б Рис. 4.4
V1/V2 = ?

Решение. Главное в задачах такого типа – давления в левой и правой половинах сосуда всегда равны, если поршень неподвижен. Запишем уравнения Клайперона для левой и правой половины сосуда (рис. 4.4,б) и получим:

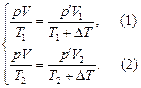
Разделим равенство (1) на равенство (2), тогда

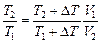Þ .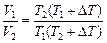

Читатель: Что меньше: V₁ или V₂?

Автор: Разделим числитель и знаменатель на (Т₁Т₂), получим

.

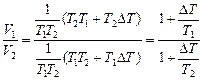Так как по условию задачи Т₁ < Т₂, то V₁ > V₂. Это значит, что поршень сместится вправо.

Ответ: .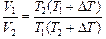

Стоп! Решите самостоятельно: В9, С11, С12.