Аналитический критерий устойчивости

Стационарные состояния биологических систем. Множественность стационарных состояний. Устойчивость стационарных состояний. Примеры.

Одним из важнейших свойств открытых биосистем является установление в них стационарных состояний в отличие от термодинамического равновесия, свойственного изолированным системам. Наиболее важным свойством стационарного состояния является его устойчивость. Эта устойчивость определяется способностью системы самопроизвольно возвращаться в стационарное состояние после внесения внешних возмущений, отклоняющих систему от исходной стационарной точки.

Устойчивость стационарной точки.

Возьмем простейшую открытую систему:

А→^υприта→^υотт

в которую поступает вещество а из внешнего резервуара с постоянной скоростью υприт = const.

Уравнение для системы имеет вид:

da/dt = υприт – υоттока = υо – ka = f(a)

В стационарном состоянии da/dt = 0, а = а (так буду обозначать стационарные точки – как подчёркивать сверху, не знаю) и υприт = υоттока

Рисунок 1

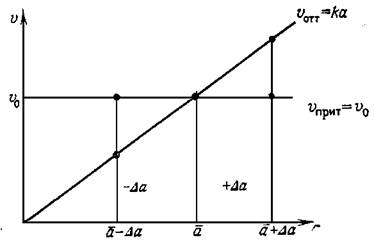
Посмотрим, устойчива ли точка. Пусть в системе произошло возмущение, сместившее систему в точку а + ∆а. Мы видим, что здесь υприт < υоттока, а значит в системе будут самопроизвольно уменьшаться и концентрация вещества, и υприт , пока снова не установится равновесие скоростей. Аналогичные рассуждения проводим для ситуации а - ∆а. Таким образом, случайные отклонения от стационарной точки компенсируются самой системой, которая находится в устойчивом стационарном состоянии.

Аналитический критерий устойчивости

Возьмем простейшую математическую модель, которой в общем виде соответствует одно дифференциальное уравнение первого порядка:

da/dt = f(a), где правая часть может иметь любой вид.

Пусть система обладает стационарной точкой а = а, где da/dt |(а = а) = 0, и следовательно f(a)= 0

Дадим отклонение ε такое, что разность ε = а – а – небольшая величина

|ε/а| = |( а - а)/а| << 1

Подставим а = а + ε в диффур. Получаем

d(а + ε )/dt = dε/dt (что da/dt = 0 надеюсь, всем понятно) = f(а + ε )

Получившуюся функцию разложим в ряд Тейлора около точки а

dε/dt = f(а + ε ) = f(а) + (df/da) а = а * ε + 0,5(d²f/da²) а = а * ε² +…

Так как в стационарной точке f(a)= 0, то ограничиваясь величиной I порядка найдём, что

dε/dt = f’(a)| a *ε

Это уравнение определяет поведение во времени возмущения ε около стационарной точки. Изменение ε = ε(t) имеет вид:

ε = εо*exp(f’a(а)*t), где εо – начальное отклонение при t=0

Видно, что если f’a(а)<0, то ε→0 при t→∞, а значит, отклонение со временем исчезает и стационарная точка устойчива. Аналогично, при f’a(а)>0 отклонение со временем будет расти.

Несколько стационарных точек.Всложной системе могут протекать реакции второго и более высоких порядков. Тогда в алгебраическом уравнении f(a)= 0 для определения координат стационарной точки появится несколько корней, это соответствует тому, что наша система может обладать несколькими стационарными состояниями.

Рассмотрим модель проточного культиватора, где концентрация с меняется из-за того, что происходит размножение бактериальных клеток (gс²), их гибель (-bс) и приток извне с заданной постоянной скоростьюVo, которую мы можем менять при необходимости. Модель имеет вид

dc/dt = Vo – bc + gс² = f(c). Пусть для простоты g = 1

Приравнивая уравнение к нулю найдём, что система имеет 2 стационарные точки:

c1 = b/2 + √(b²/4 – Vo)

c2 = b/2 - √(b²/4 – Vo)

Точка c1 неустойчива, т. к. f’(c1) = 2 c1 – b = 2√(b²/4 – Vo) > 0

В зависимости от величины Vo может меняться число стационарных точек. При Vo< b²/4 возможны два стационарных режима, при Vo= b²/4 имеется лишь одно стационарное состояние, а при Vo> b²/4 их вообще нет. Таким образом, значение Vo= b²/4 является бифуркационным, а параметрVo – управляющим.