Цель синусоидального тока с активным сопротивлением и емкостью
1.Рассмотрим цепь с последовательным соединением активного сопротивления R и емкости C (рис.76) под воздействием
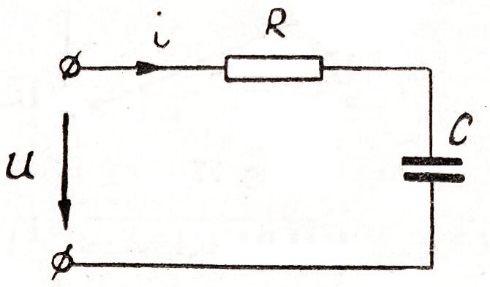
Рис. 76
синусоидального напряжения. Уравнение равновесия напряжений для этой цепи имеет вид:

Если принять начальную фазу тока равной нулю, то выражение 3.48 будет иметь вид:

Здесь
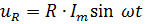
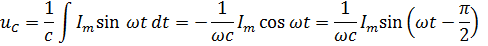
Напряжения на активном сопротивлении и на емкости изменяются по синусоидальному закону. Действующее значение напряжения на активном сопротивлении равно IR, а на емкости 
Так как напряжение на активном сопротивлении совпадает по фазе с током, а напряжение на емкости отстает от тока на угол 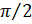 , то векторная диаграмма для действующих значений тока и напряжения в цепи R, C имеет вид, показанный на рис.77. Из треугольника напряжений:
, то векторная диаграмма для действующих значений тока и напряжения в цепи R, C имеет вид, показанный на рис.77. Из треугольника напряжений:
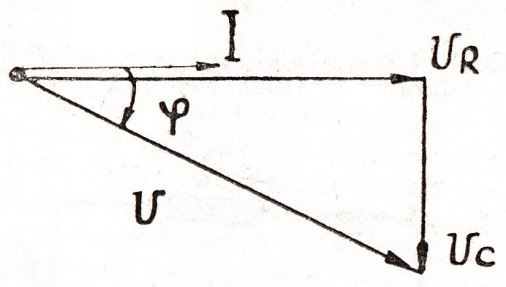
Рис. 77
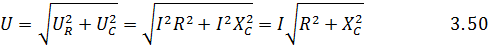
Из выражения 3.50 получим формулу закона Ома для действующих значений напряжения и тока в цепи R, C:

Величина  имеет характер и размерность сопротивления и называется полным сопротивлением цепи R, C.
имеет характер и размерность сопротивления и называется полным сопротивлением цепи R, C.
Если все стороны треугольника напряжений разделить на величину тока в цепи, то получится треугольник сопротивлений, подобный треугольнику напряжений (рис.78). Из треугольника сопротивлений

Рис. 78

Так как в цепи R, С ток опережает напряжение, то угол сдвига фаз будет отрицательным. При 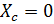 характер цепи чисто активный
характер цепи чисто активный 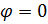 , а при
, а при 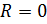 характер цепи чисто емкостной (
характер цепи чисто емкостной (  Следовательно, в цепи с последовательным соединением R и С
Следовательно, в цепи с последовательным соединением R и С

2. Мгновенная мощность в цепи R, C равна произведению мгновенных значений напряжения тока:
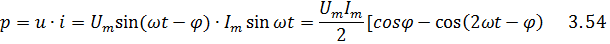
Средняя за период мощность (активная мощность) в цепи R, C равна

Так как среднее значение синусоидальной функции за период равно нулю

Умножив все стороны треугольника напряжений на величину тока в цепи, получим треугольник мощностей (рис.79). Из треугольника мощностей:
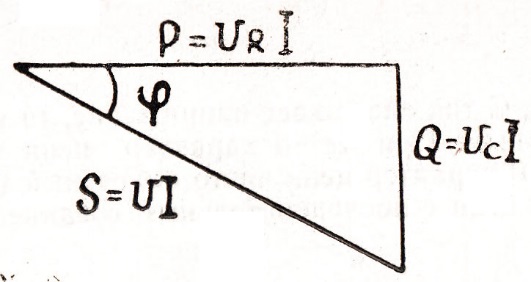
Рис. 79
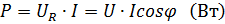


Так же, как в цепи R, L в цепи R, C имеет место необратимое преобразование электрической энергии (активная мощность) и колебания энергии между источником и емкостью (реактивная мощность). Учитывая формулы закона Ома (3.18 и 3.34), выражение для активной и реактивной мощностей можно записать следующим образом:
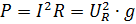
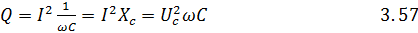
Пример 20: Конденсатор, емкость которого C=33,2 мкФ, соединен последовательно с резистором R=16 Ом.
Определить полное сопротивление цепи и ток, если к цепи подключен источник синусоидального напряжения U=200 В, частота f=400 Гц.
Решение:

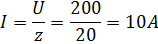
Пример 21. Цепь, состоящая из конденсатора с емкостью C= 80 мкФ и реостата с сопротивлением R=30 Ом находится под напряжением
U=120 В с частотой f= 50 Гц. Определить ток в цепи, активную и реактивную мощности, напряжения на конденсаторе и на реостате.
Решение:
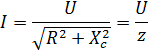


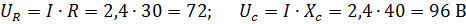

Дата добавления: 2016-04-06; просмотров: 1759;
