Цель синусоидального тока с параллельным соединением активного сопротивления, индуктивности и емкости

Согласно первому закону Кирхгофа для параллельной цепи (рис.85)

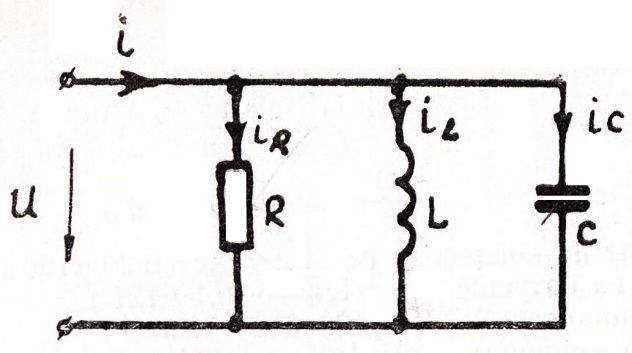Рис. 85

Так как

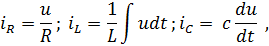
уравнение 3.67 можно записать в следующем виде:

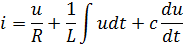
При синусоидальном напряжении с начальной фазой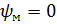

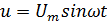
общий ток цепи представляется суммой трех синусоид:

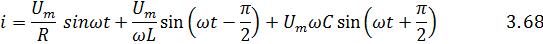
Следовательно, при синусоидальном напряжении ток в цепи с параллельным соединением R, L, C также изменяется по синусоидальному закону. Построим векторную диаграмму для действующих значений тока и напряжения (рис.86). Активная составляющая

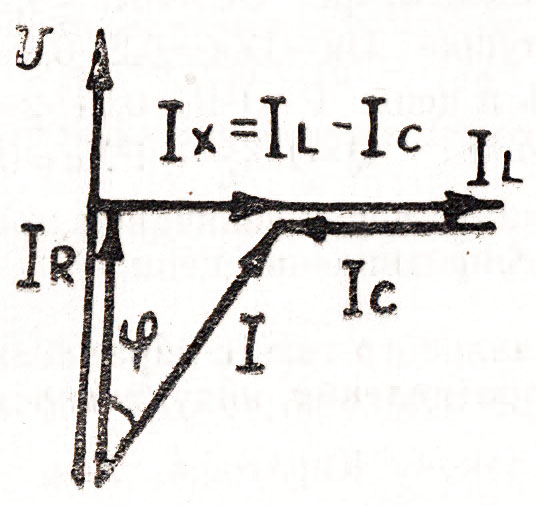Рис. 86

общий ток 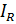совпадает по фазе с напряжением, индуктивно составляющая 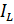отстает от напряжения на угол 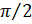и емкостная составляющая 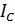опережает напряжение на угол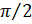

Векторная диаграмма называется треугольником токов. Из треугольников токов

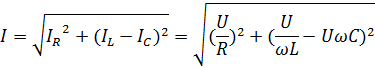
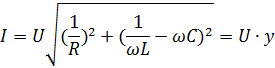
Величина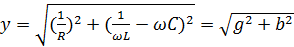

называется полной проводимостью цепи.

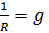- активная проводимость (Сим)

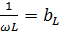-индуктивная проводимость (Сим)

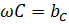- емкостная проводимость (Сим)

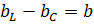-реактивная проводимость (Сим)

Из треугольников токов видно, что общий ток I (ток неразветвленной части цепи) слагается из двух составляющих:

-активной составляющей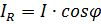

-реактивной составляющей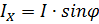

Если все стороны треугольника токов разделить на величину напряжения U, то получим треугольник проводимостей, подобный треугольнику токов (рис.87).

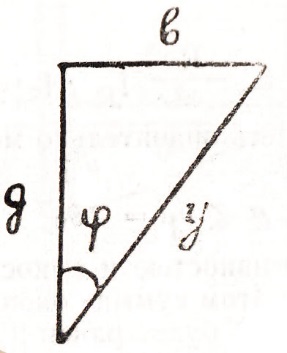Рис. 87

Один катет треугольника проводимостей пропорционален активной проводимости g, второй катет-реактивной проводимости b, а гипотенуза-полной проводимости цепи y.

Из треугольника проводимостей видно, что разность фаз напряжения и тока 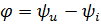равна:

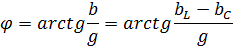
Или

В зависимости от соотношения индуктивной и емкостной проводимостей в параллельной цепи R, L, C возможны три случая:

а) индуктивная проводимость более, чем емкостная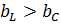

При этом угол сдвига фаз будет положительным 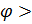0 (ток в неразветвленной части цепи отстает по фазе от напряжения), т.е. характер сопротивления цепи активно индуктивный. Векторная диаграмма, соответствующая этому случаю, показана на рис.86. Ток в ветви с индуктивностью по величине больше, чем в ветви с емкостью.

б) Индуктивная проводимость меньше емкостной

При этом угол сдвига фаз будет отрицательным (рис.88а.) 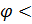0

Следовательно, ток в общей части опережает по фазе напряжение, характер сопротивления цепи активно-ёмкостной. Ток в ветви с индуктивностью по величине меньше, чем в ветви с конденсатором;

в) Индуктивная и емкостная проводимости равны по величине

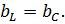Угол сдвига фаз равен нулю 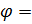0, характер сопротивления цепи чисто активный. Токи в ветвях цепи будут равны:

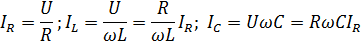
Если активная проводимость значительно меньше индуктивной или емкостной проводимостей

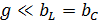
то токи в ветвях с индуктивностью и емкостью будут больше, чем общий ток в цепи. Но при этом сумма токов индуктивной и емкостной ветвей (реактивный ток) будет равен нулю и ток в ветви с активным сопротивлением (активный ток) будет равен общему току цепи (рис.86б).

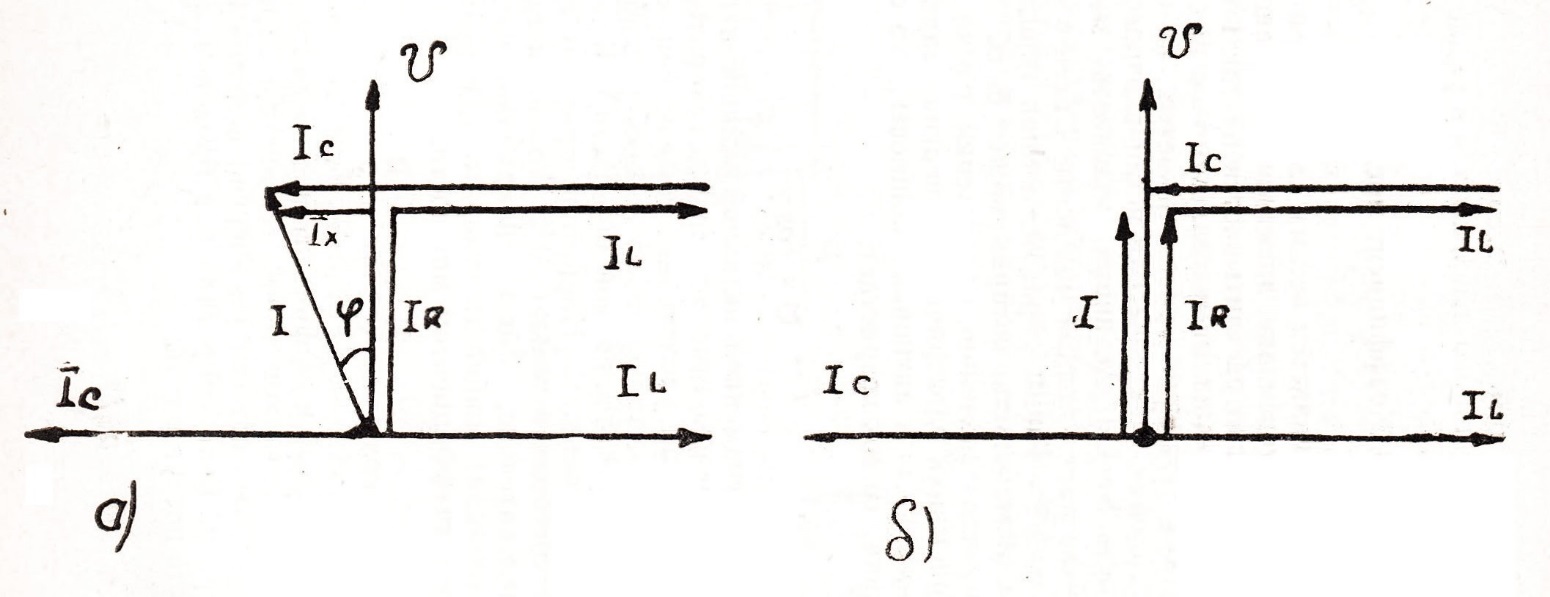
Случай, когда в параллельной цепи индуктивная проводимость равна емкостной проводимости, называется резонансом токов. Явление резонансов тока широко используется в радиотехнике.