Закон Ома для всей цепи, для пассивного и для активного

Участков цепи

1. Рассмотрим простейшую схему электрической цепи постоян­ного тока, состоящую из двух участков: внутреннего с сопротивле­нием г₀и внешнего с сопротивлением R_h.Сопротивление 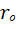пред­ставляет собой внутреннее сопротивление источника э.д.с., а сопротив­ление R_h - сопротивление нагрузки (приемника электрической энер­гии).. Электрический ток, проходя по всей цепи, преодолевает со­противление как внешнего участка, так и внутреннего. Следова­тельно э.д.с. источника идет на покрытие внутренних и внешних по­терь напряжения в цепи.

Зависимость между напряжением (э.д.с.) и током для такой цепи определяется формулой закона Ома

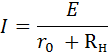
1. 5

Из этого равенства следует

Е=I 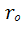+ 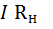, где I 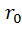- падение напряжения внутри источника

U = I 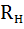- падение напряжения на внешнем участке цепи или напряжение на зажимах источника (на зажимах ab рис. 7).

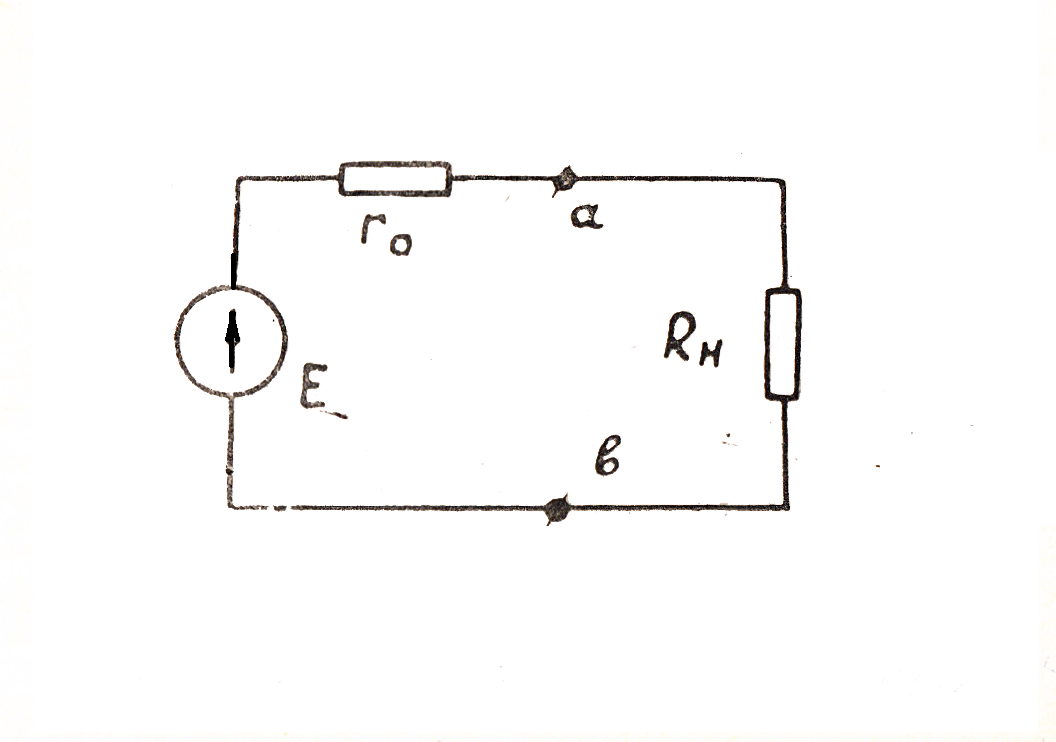
Рис. 7

2.Для пассивного участка цепи зависимость между током и напряжением определяется из выражения для падения напряжения на внешним участке цепи и имеет вид:

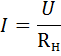
1. 6

Рассмотрим участок какой-либо сложной цепи, содержащий источник э.д.с. Определим напряжение между точками а и b актив­ною участка цепи (рис. 8)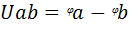

Потенциал точки «с» выше потенциала точки «а» на величину э.д.с. т. е.

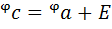
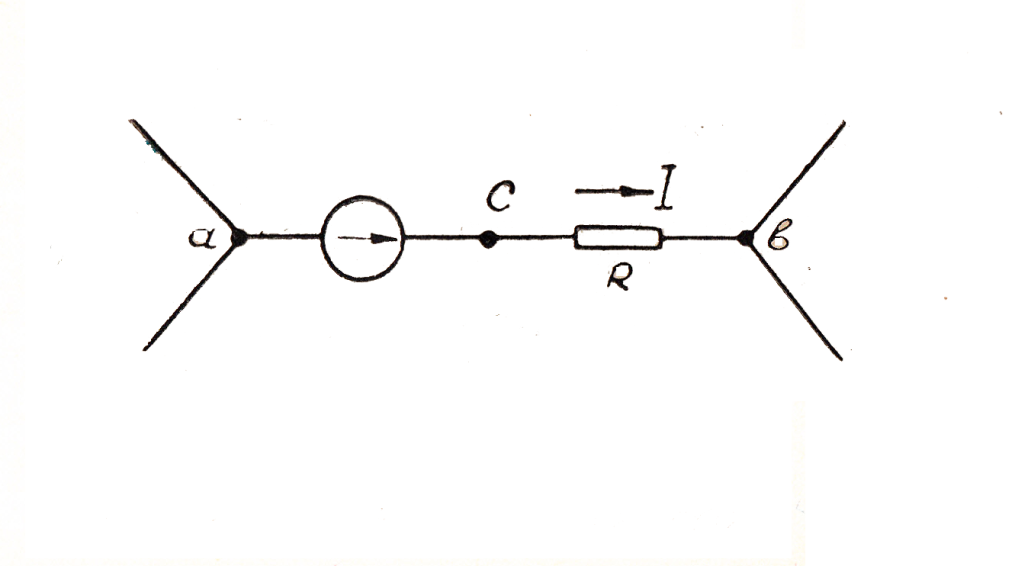
Рис. 8

Потенциал точки b ниже потенциала точки «с» на величину падения напряжения на сопротивлении R

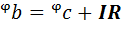
Разность потенциалов точек а и b определяет напряжение Uab и равна:

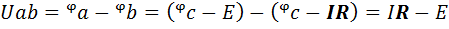
Из полученного выражения ток на участке аb равен

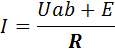
1.7

Если направление эдс не совпадает с направлением тока на рассматриваемом участке цепи, то формула 1.7 будет иметь несколько иной вид:

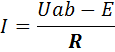
1. 8

В общем случае ток активного участка цепи, состоящего из n сопротивлений и m источников, будет равен

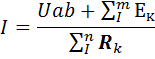
1. 9

Уравнение 1.9 выражает закон Ома для активного участка цепи и общей форме. В этом уравнении при алгебраическом суммирова­нии со знаком плюс берутся те э.д.с., направления которых совпада­ют с направлением тока и со знаком минус те э.д.с., направления которых противоположны направлению тока.

Законы Кирхгофа

Во всех участках неразветвленной электрической цепи, образую­щей замкнутый контур, постоянный ток имеет одинаковое значение.

Если же цепь разветвлена, то токи в отдельных ветвях могут быть различными, при этом суммарный заряд, притекающий к точке разветвления (узлу), всегда равен суммарному заряду, утекаю­щему от узла в течение того же времени. В этом и заключается смысл первого закона Кирхгофа, который формируется следующим образом:

алгебраическая сумма токов, сходящихся в узле равна нулю, т. е.

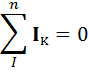
При этом токи, направленные к узлу, берут с одним знаком (например, со знаком плюс), а токи, направленные от узла - с противоположным знаком. Так, например, для узла «а» рис. 9 уравнение по первому закону Кирхгофа будет иметь вид:

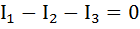или

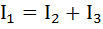
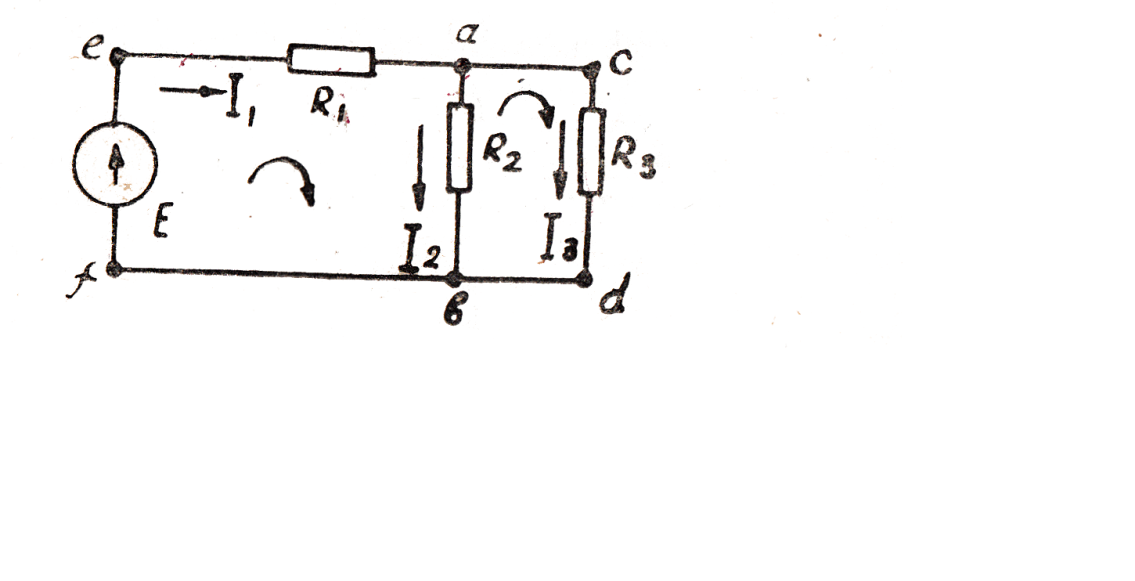
Рис. 9

Для сложных электрических цепей, состоящих из нескольких замкнутых контуров, можно составить уравнение по второму зако­ну Кирхгофа. Согласно второму закону Кирхгофа в любом замкнутом контуре сложной электрической цепи алгебраическая сумма падений напряжений на элементах этого контура равна алгебраиче­ской сумме э.д.с., входящих в данный контур.

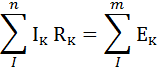
1. 11

Для составления уравнений по второму закону Кирхгофа в каждом контуре произвольно задаются направления обхода контура. Положительными считаются те э.д.с., направления которых совпада­ют с направлением обхода. Падения напряжения считаются поло­жительными, если совпадают направление тока и направление об­ходи контура. В противном случае э.д.с. и падение напряжения считаются отрицательными .Составим уравнения по второму закону Кирхгофа для цепи рис. 9:

для контура abfe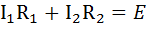

для контура acdb - 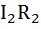+ 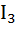R₃=0