Эквивалентные преобразования простых цепей.
При расчете цепей синусоидального тока часто возникает необходимость эквивалентного преобразования последовательного участка в параллельное и обратно.
Условием эквивалентности двух цепей является равенство полных сопротивлений (проводимостей) этих цепей и их активных и реактивных составляющих. Иначе говоря, при одинаковом напряжении на зажимах последовательной и параллельной цепи должны быть равны токи в этих цепях и углы сдвига фаз между напряжением и током.
Рассмотри две эквивалентных цепи (рис.90)
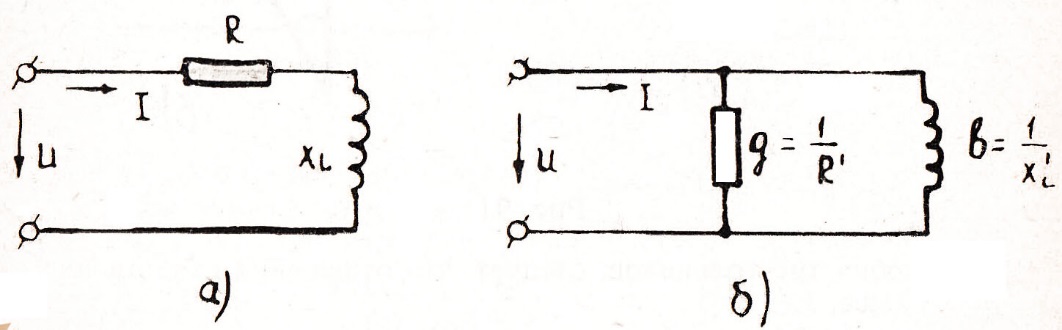
Рис. 90
Последовательная цепь характеризуется полным сопротивлением z и составляющими-активным сопротивлением R и реактивным сопротивлением 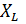 . Параллельную цепь удобнее характеризовать проводимостями-полной
. Параллельную цепь удобнее характеризовать проводимостями-полной 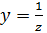 , активной
, активной 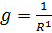
и реактивной 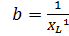
Построим для последовательной цепи треугольник сопротивлений (рис.91-а), а для параллельной цепи-треугольник проводимостей (рис.91-б). По условию эквивалентности угол 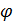 для обеих цепей один и тот же. Следовательно, треугольники сопротивлений и проводимостей подобны
для обеих цепей один и тот же. Следовательно, треугольники сопротивлений и проводимостей подобны
Из треугольника сопротивлений:

Из треугольника проводимостей:

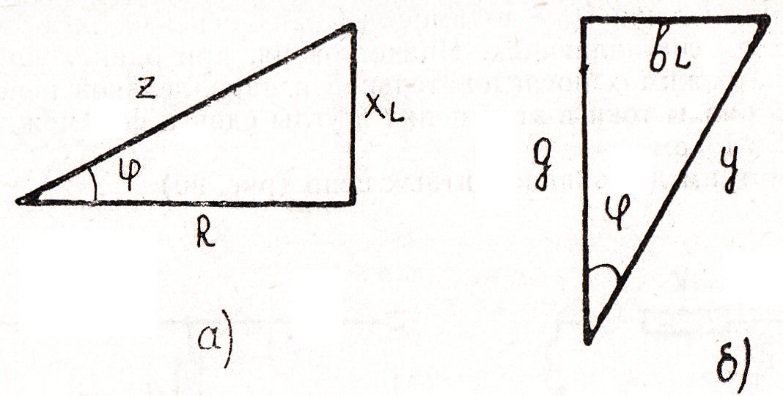
Рис. 91
Из подобия треугольников, следует, что отношения сходственных сторон равны, т.е.
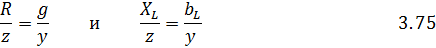
Учитывая, что для эквивалентных цепей полные сопротивления равны, можем записать

Из равенства 3.75 и 3.76 получим формулы перехода от последовательной цепи к параллельной.
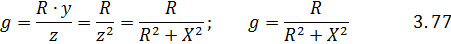
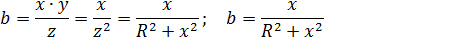
и для перехода от параллельной цепи к последовательной:
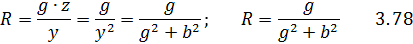
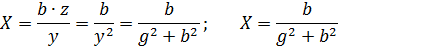
Пример 26. Дана параллельная цепь с активным сопротивлением
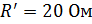 и реактивным сопротивлением индуктивности
и реактивным сопротивлением индуктивности 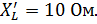
Преобразовать параллельную цепь в эквивалентную ей последовательную.
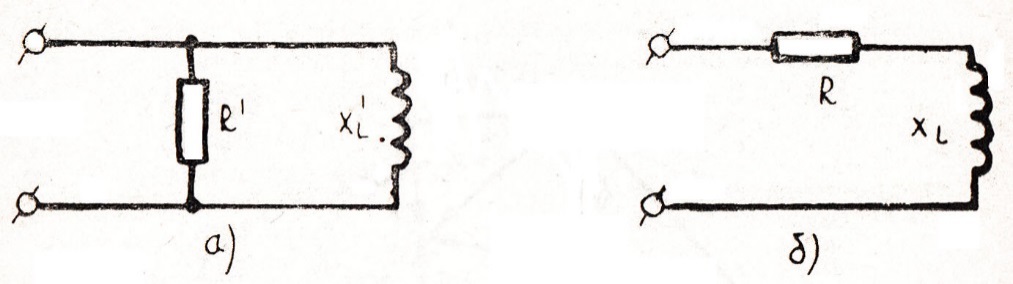
Рис. 92
Решение: Используя формулы 3. 78 определим активное и реактивное сопротивление цепи (рис.92-б).
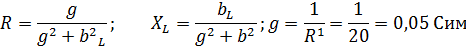
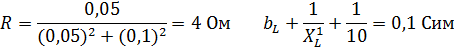
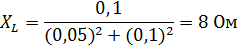
Дата добавления: 2016-04-06; просмотров: 1369;
