Принцип и метод взаимности (обратимости)
Пусть в первую ветвь Т-образной схемы, состоящей из трех сопротивлений, соединенных звездой (рис. 47а) включен источник с э.д.с. 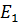 .
.
Ток 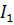 распределяется между параллельными ветвями с
распределяется между параллельными ветвями с 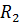 и
и 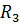 обратно пропорционально этим сопротивлениям. Ток второй ветви равен:
обратно пропорционально этим сопротивлениям. Ток второй ветви равен:
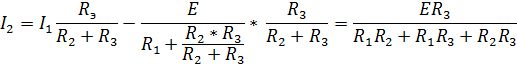
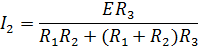
1. 31.
Перенесем источник э.д.с. во вторую ветвь (рис. 47 б) и определим ток в первой ветви.
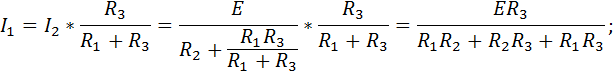
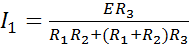 2. 32
2. 32
Сравнивая выражения 2.31 и 2.32, видим, что ток во второй ветви 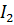 при наличии источника в первой ветви равен току первой ветви I, при переносе того же источника во вторую ветвь. Так как Т-образная схема эквивалентна любой сложной электрической цепи, не содержащей источников электрической энергии, то полученный вывод можно распространить на любую электрическую цепь с одним источником. Полученный для Т-образной схемы результат выражает так называемый принцип взаимности, который можно сформулировать следующим образом:
при наличии источника в первой ветви равен току первой ветви I, при переносе того же источника во вторую ветвь. Так как Т-образная схема эквивалентна любой сложной электрической цепи, не содержащей источников электрической энергии, то полученный вывод можно распространить на любую электрическую цепь с одним источником. Полученный для Т-образной схемы результат выражает так называемый принцип взаимности, который можно сформулировать следующим образом:
Если э.д.с., действуя в любой ветви сколь угодно сложной цепи, не содержащей других э.д.с., вызывает в другой ветви ток I то перенесенная в нее та же э.д.с. Е вызовет в первой ветви такой же ток I.
На применении принципа взаимности основан метод взаимности. Этот метод удобно применять для расчета цепей с одной э.д.с., когда ее перенос упрощает цепь.
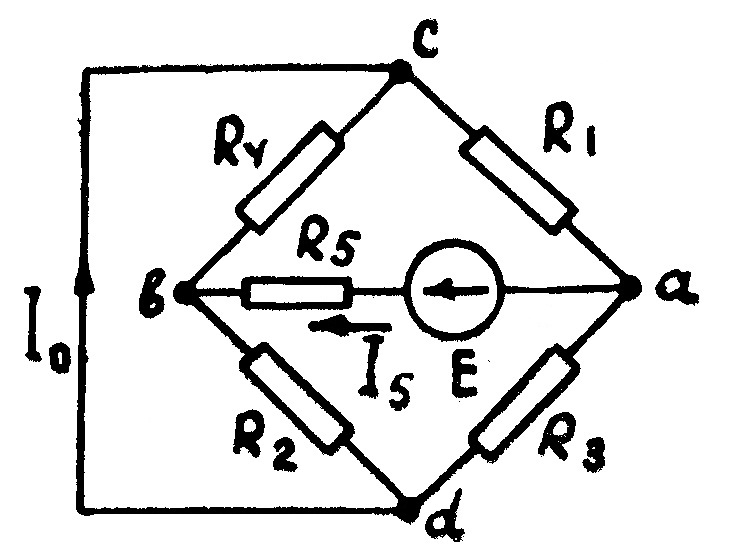
А) Рис. 48
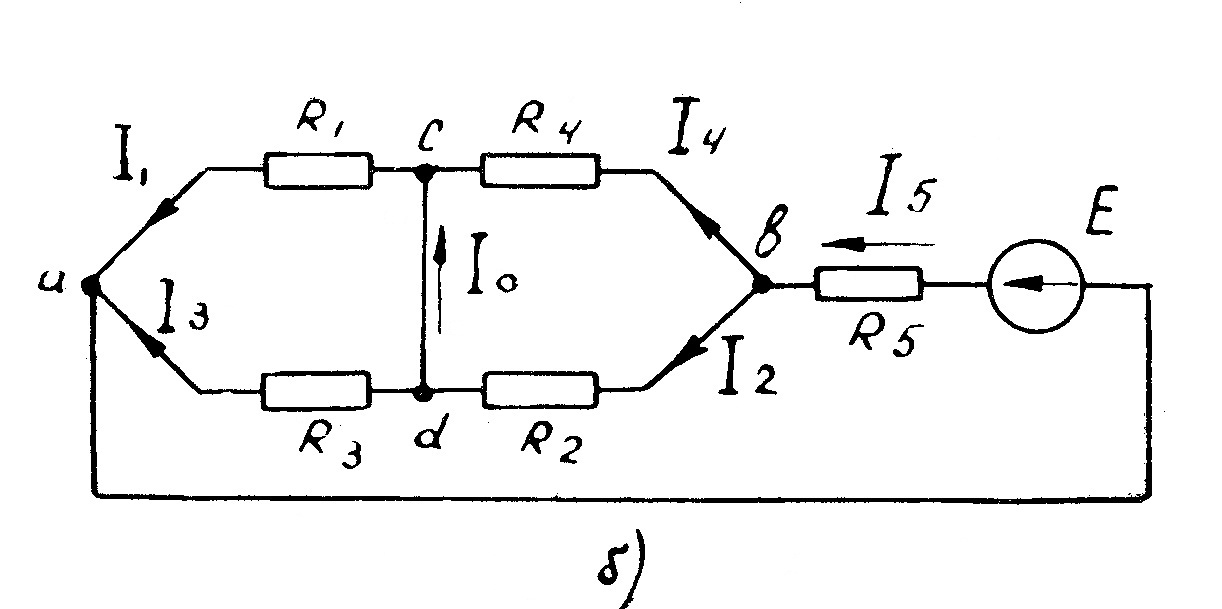
Б) Рис. 48
Пример 13. Определить ток в диагонали мостовой схемы 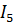 (рис. 48a), если: Е=21 B;
(рис. 48a), если: Е=21 B; 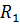 =1 Oм;
=1 Oм; 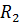 =
= 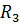 =2 Oм;
=2 Oм; 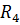 =5 Oм и
=5 Oм и 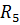 =1,9 Oм.
=1,9 Oм.
Решение: Перенесем источник э.д.с. Е в пятую ветвь (рис. 48а). При этом сложная цепь превратится в простую цепь со смешанным соединением сопротивлений. Определим ток в ветви dc. Согласно принципу взаимности такой же ток должен протекать в пятой ветви, если источник Е включен в диагональ cd.
Для схемы рис. 48 б ток 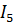 равен:
равен: 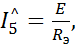 где
где
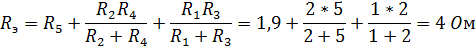
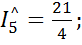
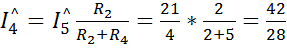
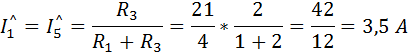
По первому закону Кирхгофа для узла «с» справедливо равенство
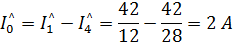
Следовательно, для исходной схемы: 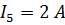
Дата добавления: 2016-04-06; просмотров: 1817;
