Теорема об эквивалентном генераторе напряжения

По отношению к выделенной ветви остальную часть цепи, представляющую активный двухполюсник, можно заменить эквивалентным генератором напряжения.

Рассмотрим теорему об эквивалентном источнике напряжения.

Теорема. Ток в любой ветви линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным

источником напряжения; э.д.с. этого источника должна быть равна напряжению на зажимах активного двухполюсника при отключенном сопротивлении выделенной ветви (Еэ= 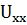), а внутреннее сопротивление источника должно быть равно

входному сопротивлению пассивного двухполюсника со стороны полюсов при отключенном сопротивлении выделенной ветви.

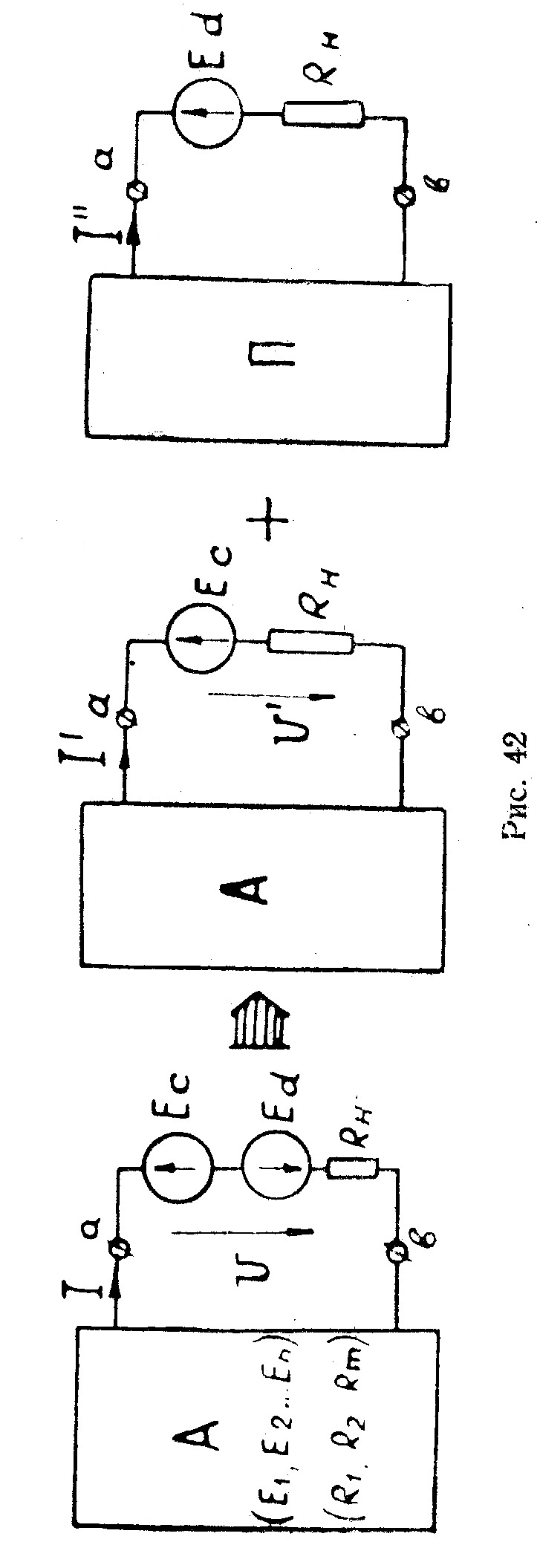
Доказательство. Возьмем как угодно сложную цепь и выделим одну ветвь с сопротивлением 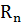. Всю остальную часть цепи представим в виде активного двухполюсника с n источниками э.д.с. и m сопротивлениями (рис. 42).

Последовательно с сопротивлением выделенной ветви 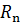включим два идеальных источника 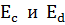с равными по величине, но противоположно направленными э.д.с.. Так как источники 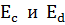компенсируют друг друга, то их включение не изменит режим работы цепи.

К полученной цепи применим метод наложения. На первом этапе определим частичный ток 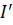, протекающий в выделенной ветви под действием всех э.д.с. активного двухполюсника и э.д.с. .

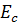На втором этапе определим частичный ток 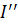, протекающий в этой же ветви под действием только.э.д.с. .

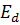Первый частичный ток равен:

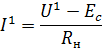
Подберем величину э.д.с. 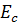так, чтобы ток 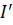был равен нулю. Это будет в том случае, если 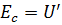. Так как при 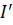=0 имеет место режим холостого хода, то напряжение 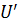является напряжением холостого хода. Следовательно: 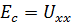. Для определения второго частичного тока 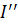заменим пассивный двухполюсник эквивалентным сопротивлением 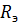, величина которого равна входному сопротивлению этого двухполюсника со стороны зажимов аb (рис. 43).

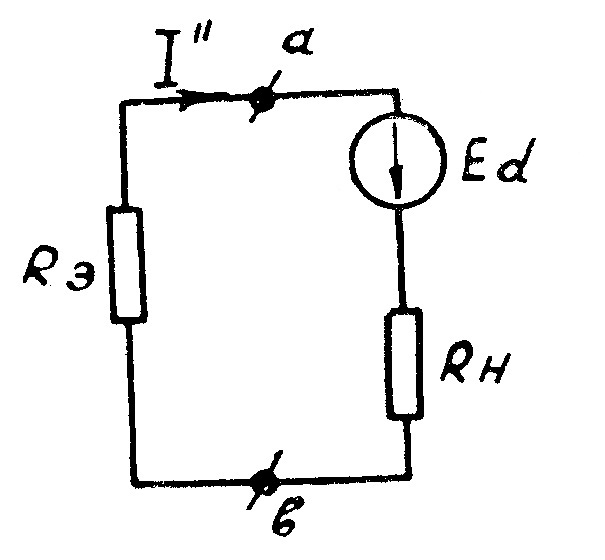Рис.43

Тогда второй частичный ток будет равен

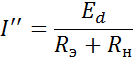
Согласно принципу наложения ток в выделенной ветви I равен сумме первого и второго частичных токов.

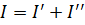или I= 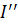, так как 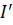=0. Следовательно

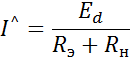
Учитывая, что 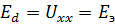, запишем окончательно:

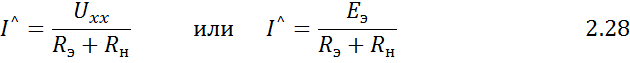
Формулы 2.28 аналогичны выражению закона Ома для полной цепи (1.5), где 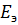представляет собой э.д.с. источника, а 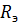- внутреннее сопротивление этого источника.

Таким образом, можно сделать вывод, что всякий активный двухполюсник может быть заменен источником с э.д.с. 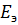и внутренним сопротивлением 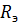. В связи с изложенным, формулу 2.28 называют формулой эквивалентного генератора напряжения. Если числитель и знаменатель формулы 2.28 разделить на величину 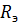, то получим:

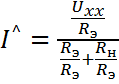2. 29

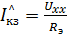Так как и 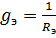, то выражение 2.29 примет вид

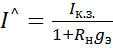2.30

Формула 2.30 называется формулой эквивалентного генератора тока.

3. Метод эквивалентного генератора

Метод эквивалентного генератора (источника) основан на использовании теоремы об эквивалентном источнике. Этот метод позволяет представить сложную электрическую цепь с произвольным количеством источников электрической энергии в виде простой цепи с одним эквивалентным источником. Метод эквивалентного генератора целесообразно применять в тех случаях, когда выделение одной ветви значительно упрощает оставшуюся часть цепи. Особенно удобен этот метод для определения тока в одной ветви сложной электрической цепи при нескольких значениях сопротивления в этой ветви. Такая задача довольно часто встречается на практике, так как нагрузка обычно бывает переменной. 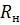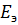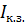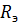В этом случае в формулах эквивалентного генератора (2.28 и 2.30) изменяют лишь значения сопротивления выделенной ветви ( ), оставляя без изменения остальные один раз вычисленные для этой цепи величины (параметры цепи) или и или .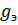

Таким образом, расчет цепи методом эквивалентного генератора сводится к определению параметров цепи. Параметры эквивалентного генератора (цепи) можно определить аналитическим (расчетным) и опытным (экспериментальным) путем.

Для определения напряжения холостого хода (э.д.с. эквивалентного генератора 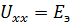) аналитически следует отключить сопротивление рассматриваемой ветви ( 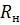), а затем любым из известных методов (методом контурных токов, узловых потенциалов, преобразований и т. п.) рассчитать напряжение между точками цепи, к которым была подключена выделенная ветвь.

Для определения напряжения холостого кода опытным путем следует отключить сопротивление выделенной ветви и вместо него подключить вольтметр (рис. 44«а», «б»).

Измеренное вольтметром напряжение есть напряжение холостого хода активного двухполюсника 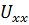или э.д.с. эквивалентного генератора .

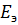При вычислении аналитическим путем сопротивления эквивалентного генератора 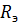необходимо мысленно закоротить все источники э.д.с., оставив в схеме их внутренние сопротивления (если они заданы), и отключить сопротивление выделенной ветви. Затем подсчитать сопротивление пассивного двухполюсника относительно тех точек, к которым была подключена выделенная ветвь (на рис. 44 между точками а и b). В случае необходимости для вычисления использовать преобразование треугольника сопротивлений в звезду или наоборот—звезды в треугольник.

Для определения внутреннего сопротивления эквивалентного генератора нужно замерить напряжение холостого хода 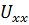(рис.44) и ток короткого замыкания (для этой цели вместо вольтметра между точками а и b рис. 44 включить амперметр).

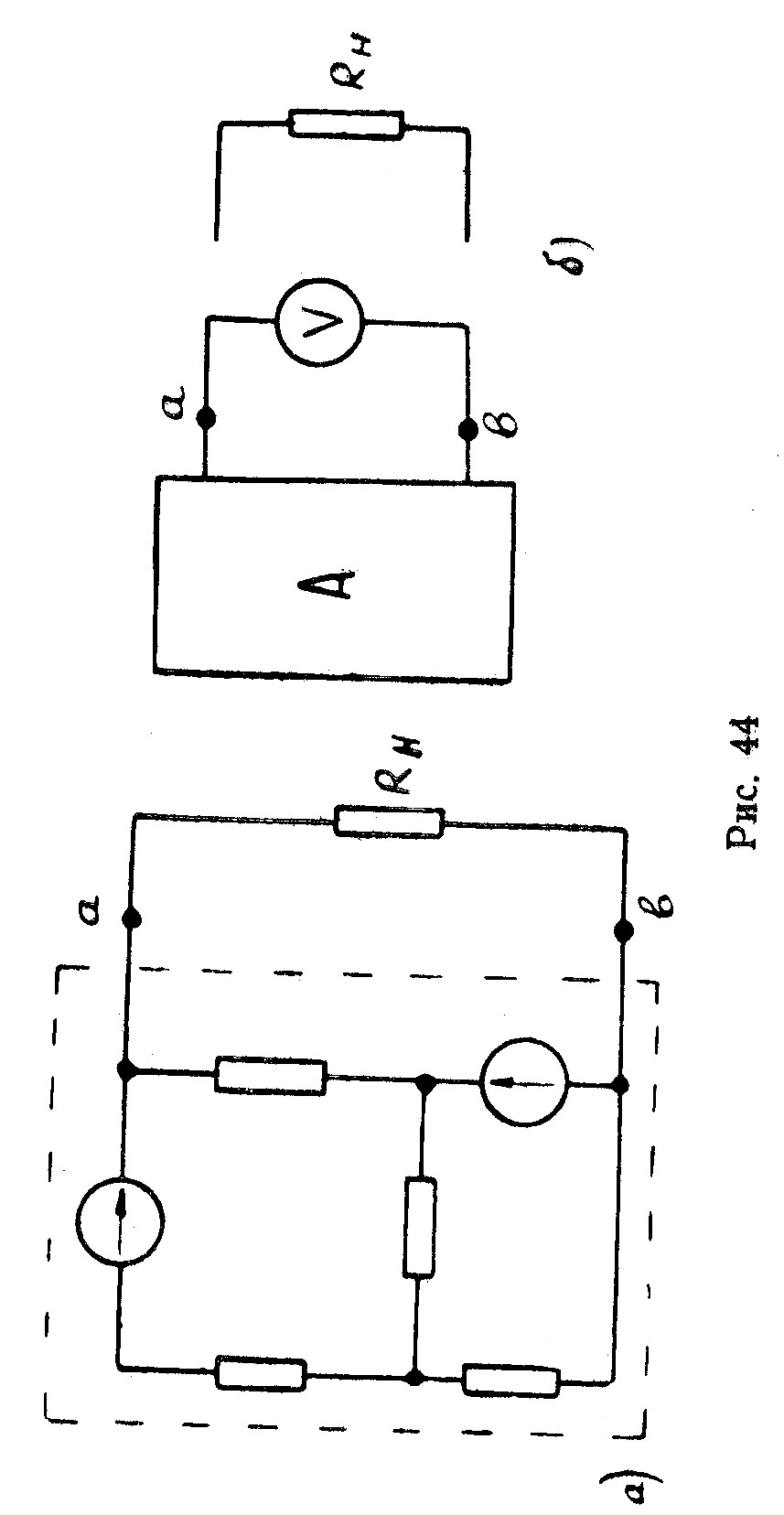
По формуле закона Ома подсчитать сопротивление:

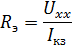
Таким образом, расчет методом эквивалентного генератора напряжения производится в следующей последовательности:

а) определение напряжения холостого хода на зажимах активного двухполюсника (э.д.с, эквивалентного генератора) ;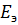

б) определение входного сопротивления пассивного двухполюсника (внутреннего сопротивления эквивалентного генератора) относительно его зажимов ;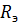

в) определение тока в выделенной ветви по формуле эквивалентного генератора напряжения 2.28.

Пример 12. Определить ток 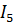в диагонали мостовой схемы (рис. 45), если Е=21 B, 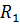=1 Oм, 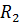= =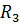2 0м, 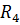=5 Oм, 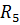=1,9 Oм, и 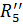=7,9 Oм.

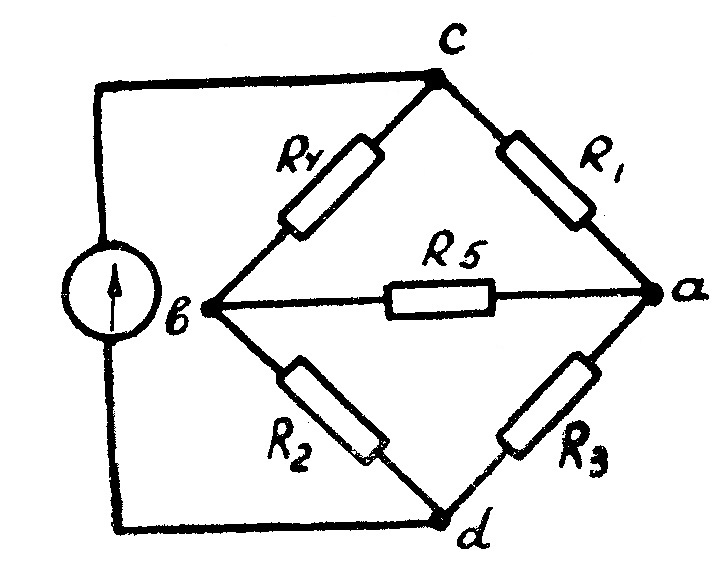Рис. 45

Решение: Выделим ветвь с сопротивлением 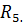Остальную часть схемы, представляющую активный двухполюсник, заменим эквивалентным источником э.д.с. (генератором).

Э.д.с. эквивалентного источника равна напряжению холостого хода 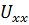на зажимах ab при отключенном сопротивлении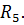

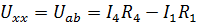
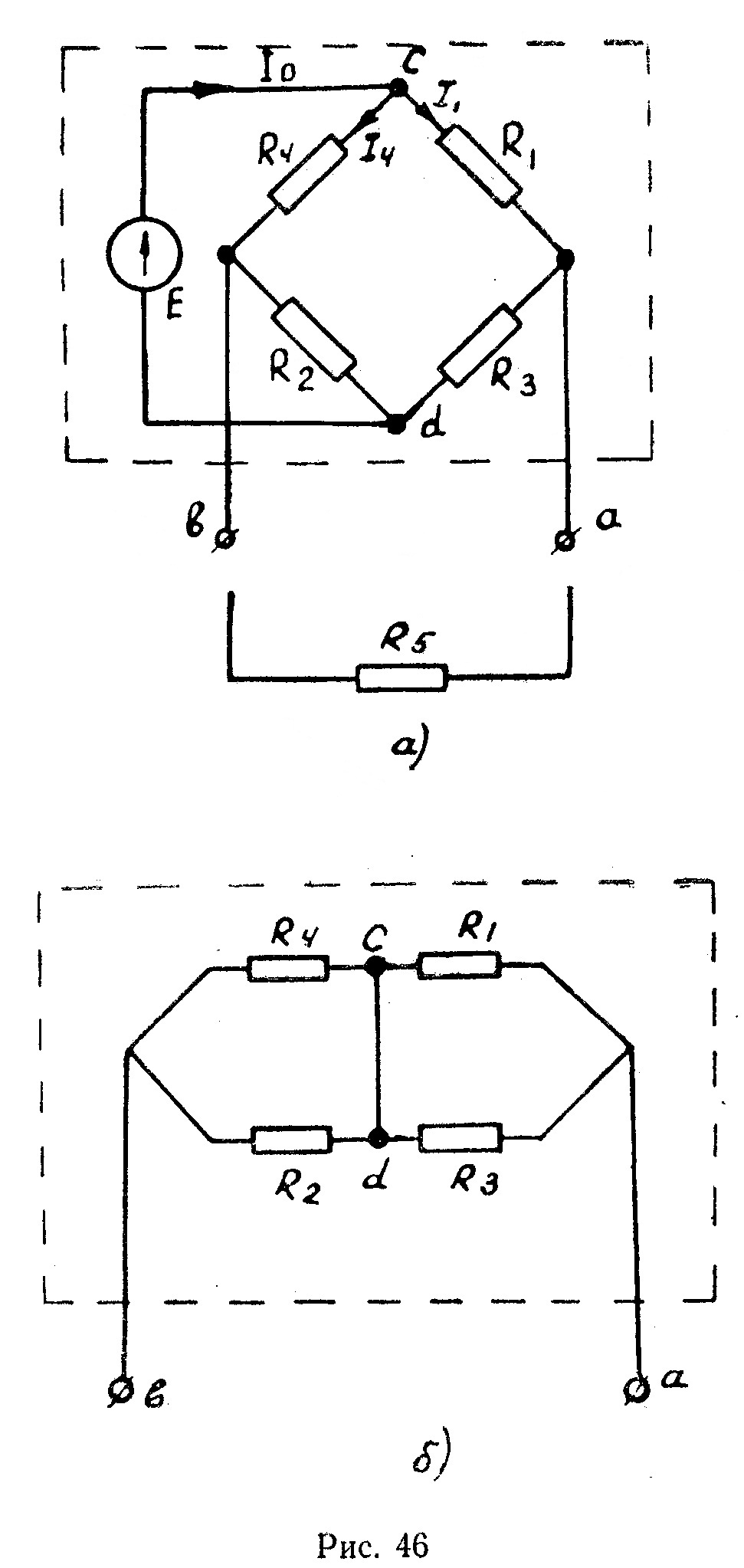
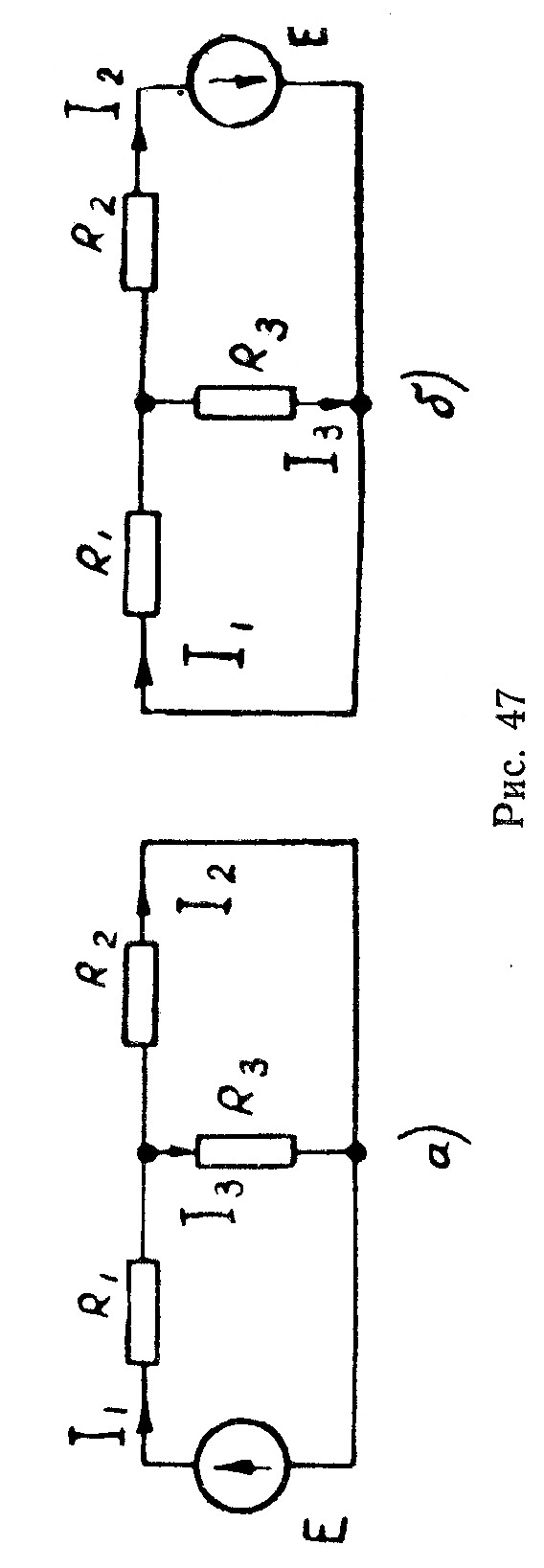
При отключенном сопротивлении 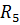цепь превращается в простую цепь (рис. 4б а), где

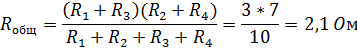
Общий ток 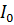неразветвленной части цепи равен:

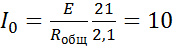А

Токи в ветвях 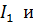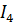равны:

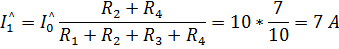
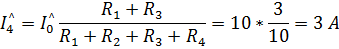
Напряжение холостого хода :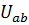

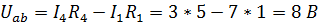
Следовательно,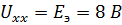

Внутреннее сопротивление эквивалентного источника равно входному напряжению пассивного двухполюсника (при закороченном источнике Е) относительно зажимов аb (рис. 46б)

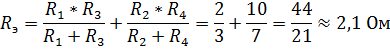
По формуле 2.28 находим ток 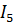, если: