Метод преобразования

С целью упрощения расчета сложной цепи в ряде случаев целесообразно осуществить эквивалентное преобразование некоторой части цепи. Эта часть цепи эквивалентна после преобразования той же части до преобразования в том случае, если режим незатронутой преобразованием части цепи остался неизменным. К числу таких преобразований относятся преобразование соединения треугольником в соединение звездой, преобразование соединения звездой в эквивалентное соединение треугольником, преобразование нескольких параллельно соединенных ветвей с источниками э.д.с. в. эквивалентную им ветвь с одним источником э.д.с. и т.п.

I. Преобразование соединения треугольником в эквивалентное соединение звездой

В сложных цепях могут встретиться такие участки цепи, соединение элементов в которых не относится ни к последовательному, ни к параллельному. Такие участки могут представлять собой соединение треугольником или звездой (рис. 34 а, б).

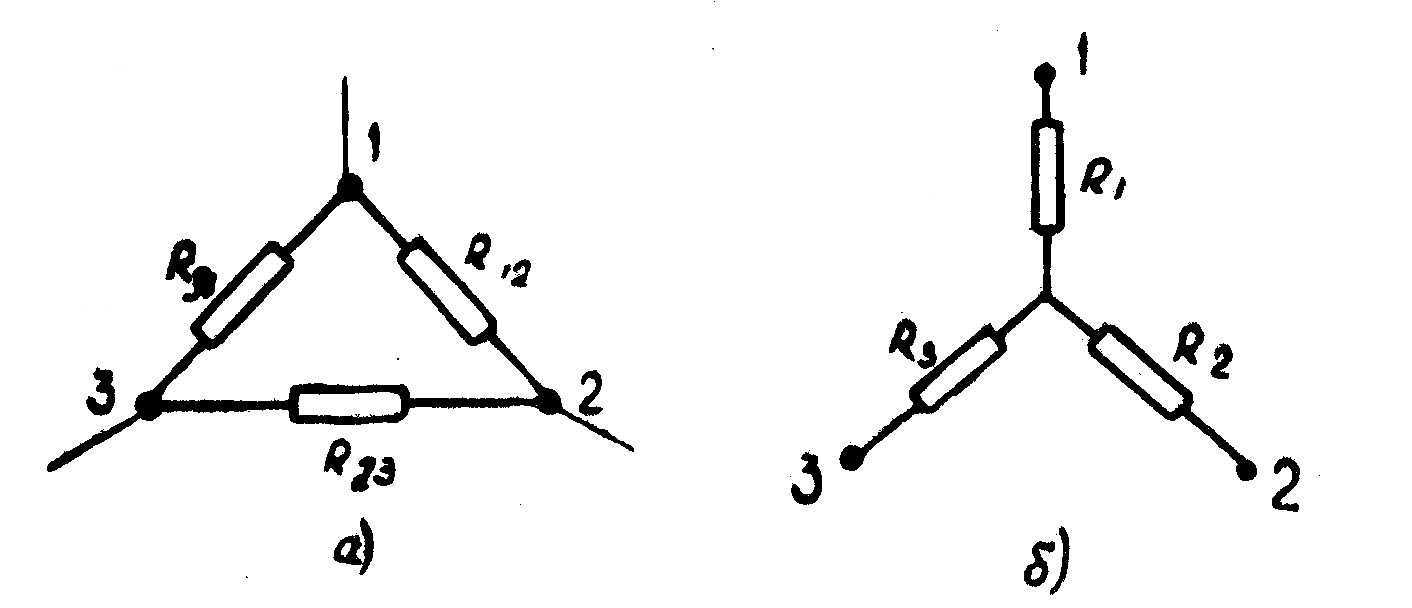
Рис. 34

В большинстве случаев расчет сложной цепи можно свести к расчету смешанной цепи, если соединение треугольником заменить эквивалентной ему звездой. Для эквивалентности треугольника и звезды необходимо и достаточно, чтобы результирующее сопротивление между каждой парой точек при отключенной третьей точке у обеих цепей было одинаково. Исходя из этого условия, выведем формулы для перехода от соединения треугольником к соединению звездой.

Сопротивления между зажимами 1-2 для звезды и для треугольника должны быть равны:

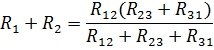
То же сiмое и между зажимами 2-З и З-1:

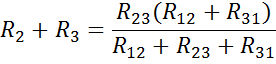
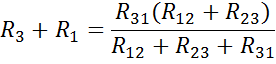
Складывая два любых уравнения и вычитая третье, получила искомые формулы:

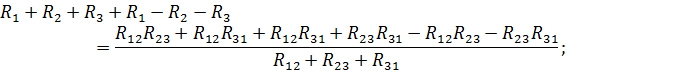
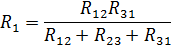
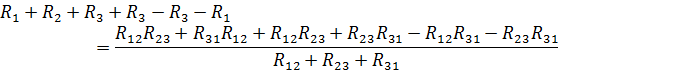
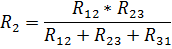
2.21

Аналогично находим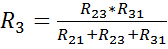

Пример 10. Определить ток в неразветвленной части цепи (рис.35), если E=30 B,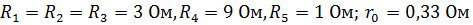

Решение: Заменим треугольник сопротивлений acd эквивалентной звездой. По формулам 2.21 вычислим сопротивления звезды:

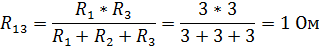
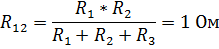
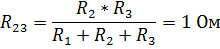
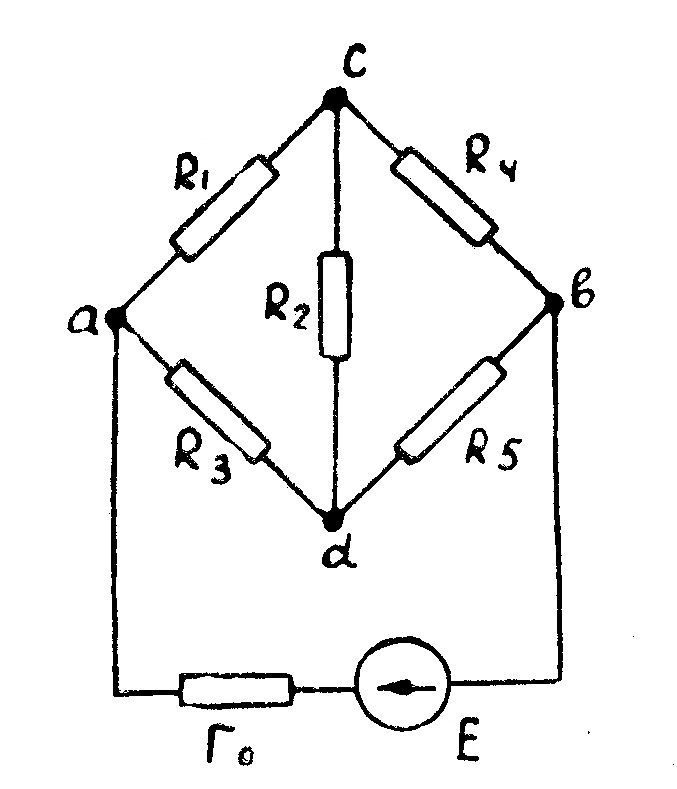
Рис. 35

В результате преобразования схема цепи будет иметь вид, показанный на схеме рис. 36. Ток в неразветвленной части цепи по закону Ома равен:

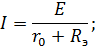
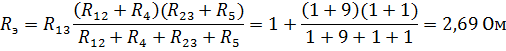
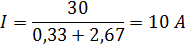
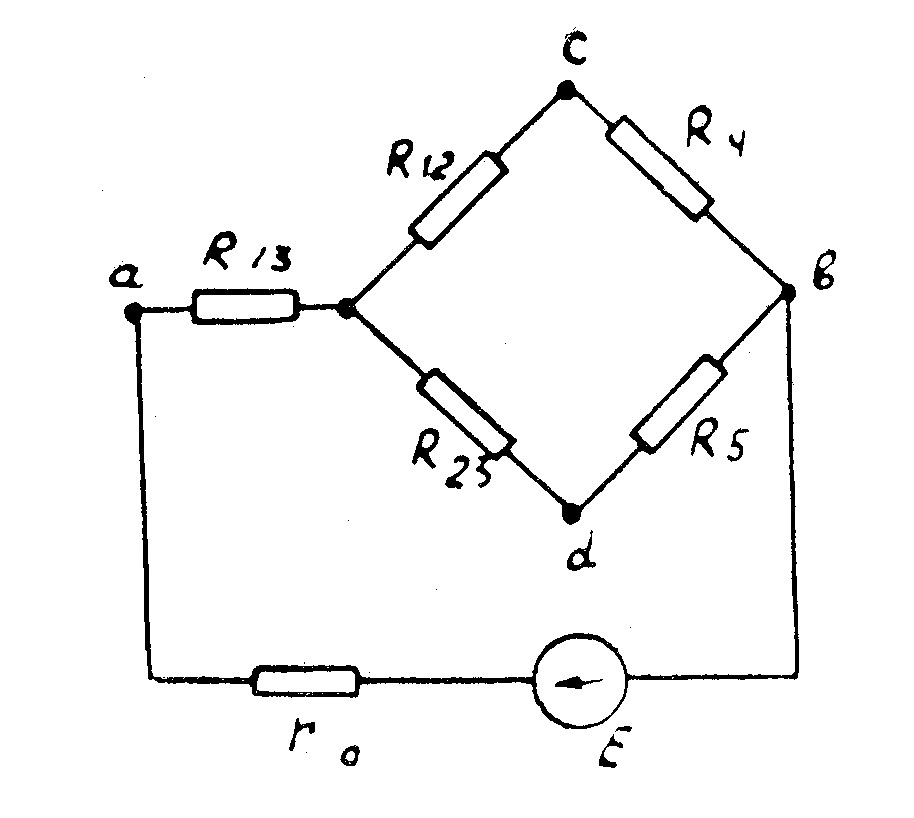
Рис. 36