Метод узловых напряжений (узловых потенциалов)
При расчете сложных электрических цепей, когда уменьшенное на единицу количество узлов меньше количества независимых контуров, целесообразно применять метод узловых потенциалов (напряжений), основанный на использовании 1-го закона Кирхгофа и закона Ома для активного участка цепи. Сущность этого метода заключается в том, что решив систему уравнений, составленных во по формулам общего вида, находят потенциалы узлов относительно базовогоузла, потенциал которого условно принят равным нулю. Затем по формулам закона Ома (1.9) вычисляют токи в ветвях. Для вывода формул общего вида рассмотрим сложную электрическую цепь (рис. 27).
В данной цепи число узлов равно 3(q=3), число ветвей 6(Р=6). Количество независимых контуров —4, следовательно q—1<4. Примем потенциал одного из узлов равным нулю (например 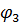 = 0)
= 0)
Далее составим уравнения по первому закону Кирхгофа для 1 и 2-го узлов, предварительно, задавшись направлениями токов в ветвях:
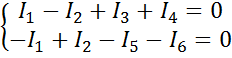
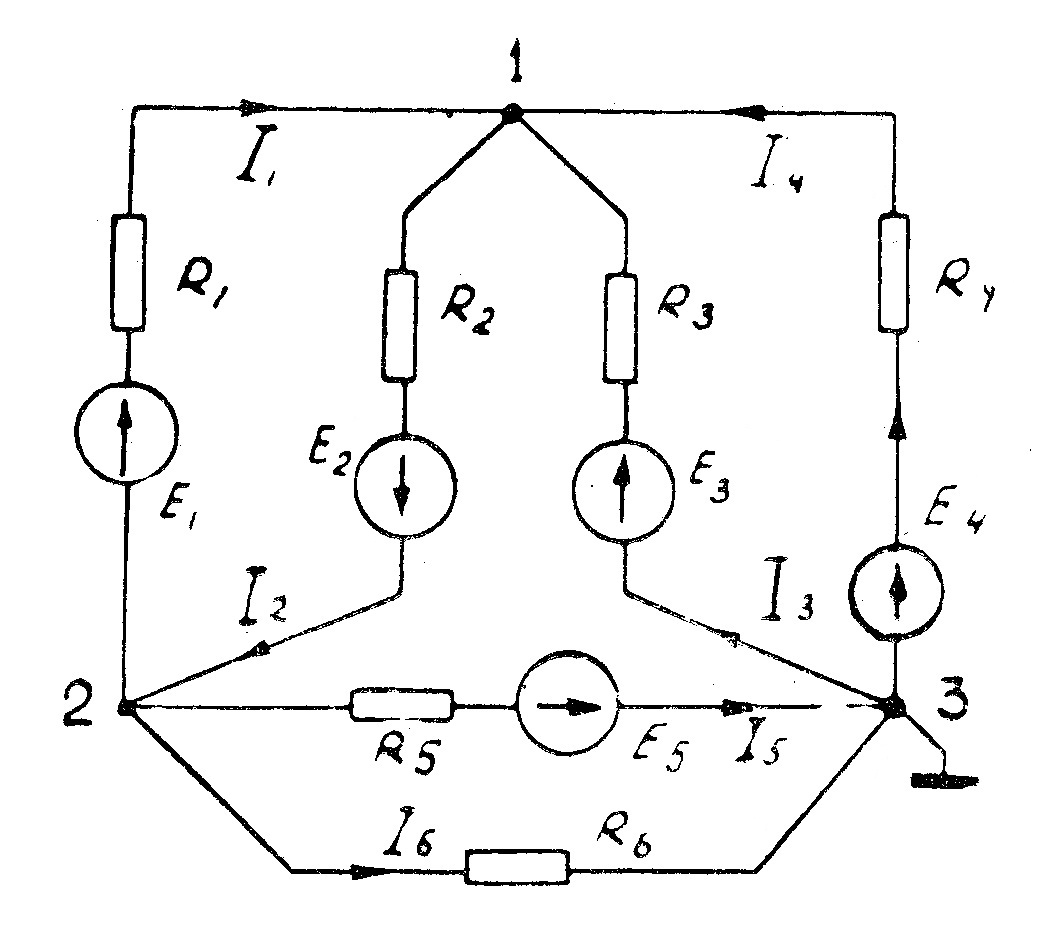
Рис. 27
По формуле закона Ома (1.9) запишем выражения для токов в ветвях:
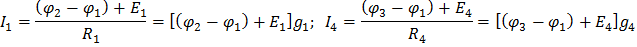
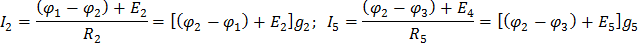
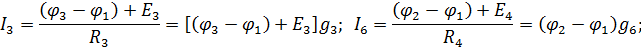
Значения токов подставим в уравнения, составленные по первому закону Кирхгофа:
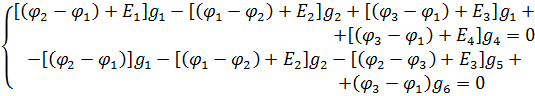
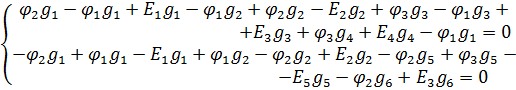
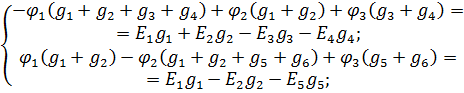
Умножим оба уравнения на минус единицу и исключим члены, содержащие
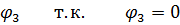
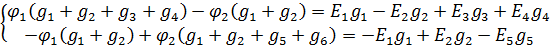
Введем обозначения:
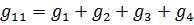 — собственная проводимость 1-го узла, равная сумме проводимостей всех вётвей, сходящихся в 1-м узле
— собственная проводимость 1-го узла, равная сумме проводимостей всех вётвей, сходящихся в 1-м узле
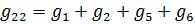 — собственная проводимость 2-го узла, равная сумме проводимостей всех ветвей, сходящихся во 2-м узле
— собственная проводимость 2-го узла, равная сумме проводимостей всех ветвей, сходящихся во 2-м узле
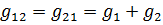 — взаимная проводимость 1-го и 2-го узлов, равная сумме проводимостей всех ветвей, соединяющих непосредственно 1-й и 2-й узлы. В уравнениях всегда берутся со знаком минус.
— взаимная проводимость 1-го и 2-го узлов, равная сумме проводимостей всех ветвей, соединяющих непосредственно 1-й и 2-й узлы. В уравнениях всегда берутся со знаком минус.
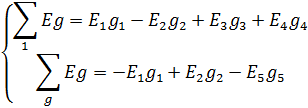
Сумма произведений э.д.с. каждой ветви, примыкающей к данному узлу, на проводимость этой ветви.
При суммировании со знаком плюс берутся э.д,с., направленные к данному узлу.
С учетом принятых обозначений система уравнений примет вид:
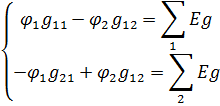
В общем случае, для цепи, имеющей n+ 1 узлов система уравнений имеет следующий вид:
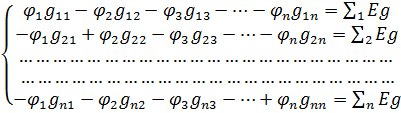 2.17
2.17
Система уравнений 2.17 и представляет собой формулы общего вида.
При расчете цепей методом узловых потенциалов следует придерживаться следующей последовательности:
а) Определить число узлов. Один из узлов условно заземлить (т. е. принять его потенциал равным нулю). Удобнее заземлять тот узел, в котором сходится наибольшее число ветвей. Задать произвольно направления токов в ветвях;
б) составить (q-1) уравнений по формулам общего вида (2.17);
в) решить систему уравнений относительно потенциалов узлов;
г) зная потенциалы узлов, по формулам закона Ома (1.9) вычислить токи в ветвях. Если значение тока для какой-либо ветви получится со знаком минус, то это значит, что направление тока в этой ветви задано неправильно.
Правильность расчета цепи проверить по первому закону Кирхгофа или, составив уравнение баланса мощностей.
В том случае, когда цепь состоит только из двух узлов, расчет методом узловых потенциалов значительно упрощается. На рис. 28 представлена схема цепи, состоящей из 4-х ветвей и двух узлов.
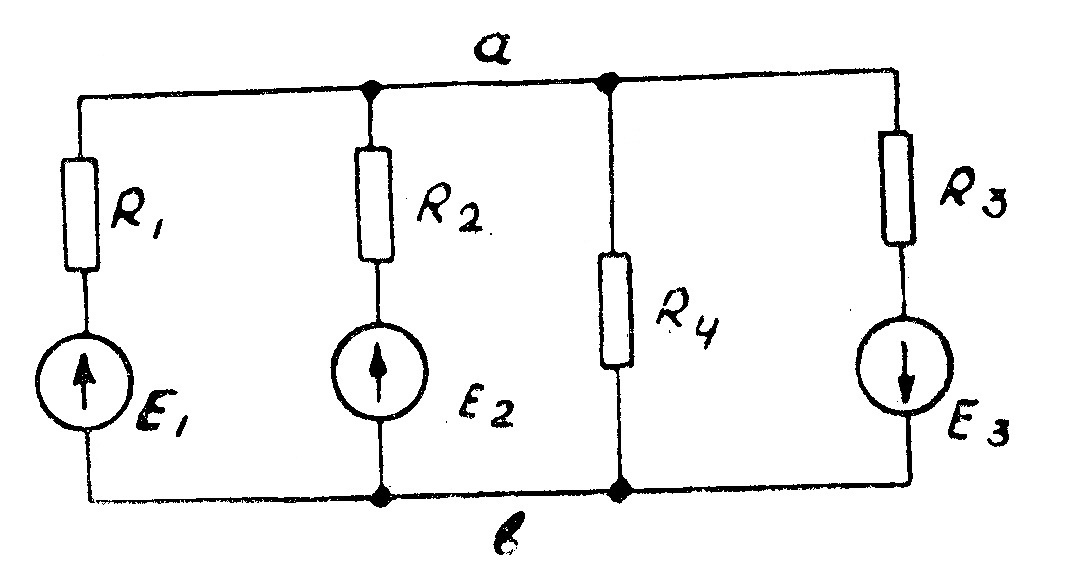
Рис. 28
Для расчета этой цепи нёобходимо составить одно уравнение
(q-1) =1.
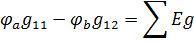
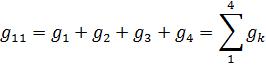
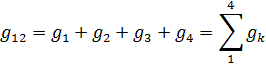
Следовательно, в данном случае 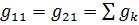
Учитывая, что 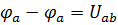 , получим
, получим
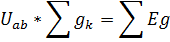
отсюда
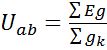 2. 18
2. 18
Зная узловое напряжение 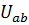 , по формулам закона Ома определяют токи в ветвях. Такой метод расчета цепей, имеющих два узла, называют методом узлового напряжения или методом двух узлов.
, по формулам закона Ома определяют токи в ветвях. Такой метод расчета цепей, имеющих два узла, называют методом узлового напряжения или методом двух узлов.
Пример 7. Определить токи в ветвях, если известны э.д.с. источников и сопротивления приемников электрической энергии:
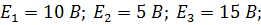
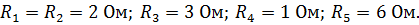
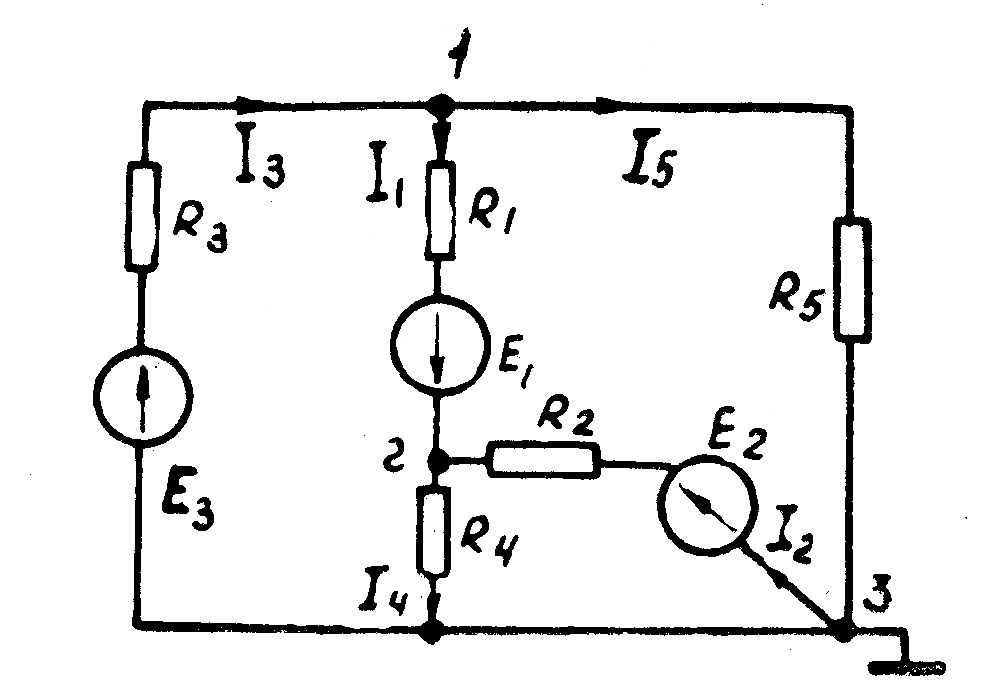 Рис. 29
Рис. 29
Решение:
а) условно заземлим узел 3 ( 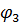 = 0);
= 0);
б) зададим направление токов в ветвях;
в) составим q-1 уравнений по формулам общего вида. Так как q=3, число уравнений будет q-1=2.
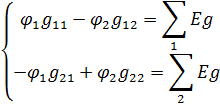
г) Подсчитаем собственные и взаимные проводимости:
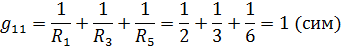
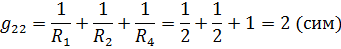
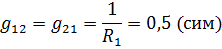
д) Вычислим суммы произведений 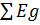
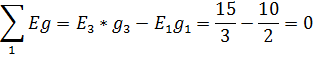
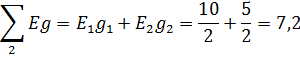
е) Вычисленные числовые значения подставим в систему уравне-ний и решим ее относительно 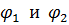
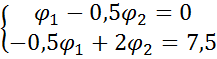
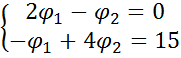
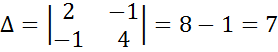


ж) Вычислим токи в ветвях по формулам закона Ома
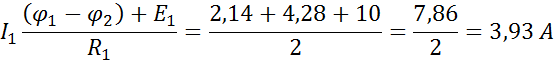
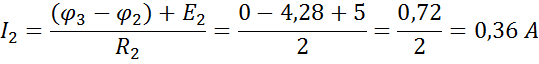
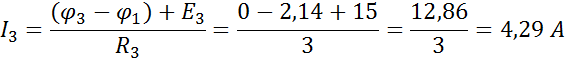
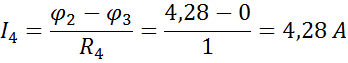
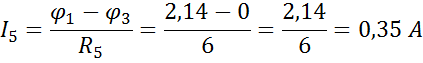
Для проверки правильности решения составим уравнение баланса мощностей:
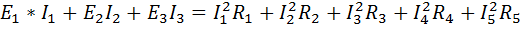
10*3,93+5*0,36+15*4,29=15,4*2+0,19*2+18,4*3+18,3*1+0,12*6
Пример 8.Определить токв ветвях, если 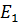 =113 B,
=113 B, 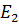 =112,5 B;
=112,5 B;
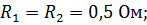
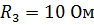
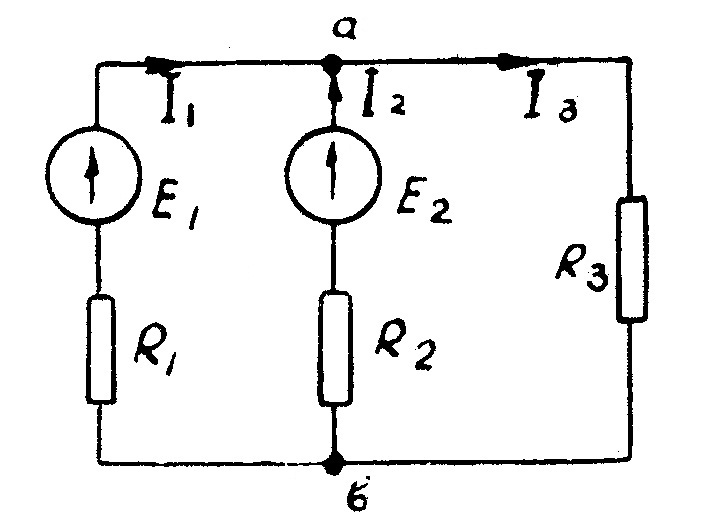
Рис. 30
Решение: Согласно формуле (2.18)
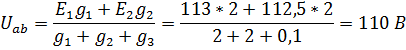
Токи в ветвях цепи:
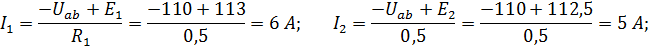
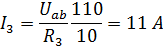
Правильность расчета проверим по первому закону Кирхгoфа:

Метод наложения
Для расчета сложных электрических цепей, содержащих несколько источников, иногда целесообразно использовать принцип наложения (суперпозиции). Принцип наложения основан на общем физическом принципе независимости действия сил в линейных системах. Применительно к линейным электрическим цепям принцип наложения состоит в том, что ток в любом участке цепи равен алгебраической сумме частичных токов, создаваемых в этом участке от всех э.д.с. цепи, действующих отдельно друг от друга.
Если для узлов и контуров электрической цепи, содержащей источники э.д.с. 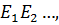 составить уравнения по первому и второму законам Кирхгофа, то получится система линейных уравнений, из которой ток в каждой ветви определяется однозначно:
составить уравнения по первому и второму законам Кирхгофа, то получится система линейных уравнений, из которой ток в каждой ветви определяется однозначно:
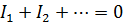
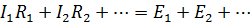 2.19
2.19
Предположим, что в цепи поочередно существуют только источник 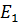 , а остальные равны нулю, затем источник
, а остальные равны нулю, затем источник 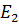 и т. д. В этом случае для вычисления токов в ветвях можно составить соответствующие системы уравнений:
и т. д. В этом случае для вычисления токов в ветвях можно составить соответствующие системы уравнений:
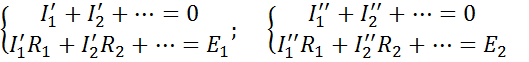 и т.д.
и т.д.
Почленное сложение этих уравнений даст систему, которая, также имеет единственное решение для всех неизвестных (например, 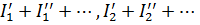 и т. д.)
и т. д.)
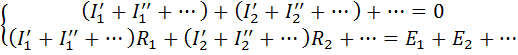 2.20
2.20
Из сравнения левых и правых частей уравнений 2.19 и 2.20 видно, что 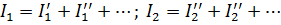 и т.д.
и т.д.
Здесь токи 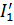 и
и 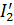 частичные токи, протекающие под действием э.д.с.
частичные токи, протекающие под действием э.д.с. 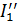 и
и 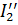 - частичные токи, протекающие под действием э.д.с.
- частичные токи, протекающие под действием э.д.с. 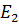 и т.д.
и т.д.
Метод наложения состоит в определении и последующем суммировании (наложении) токов в ветвях от каждой э.д.с. в отдельности. При этом остальные э.д.с. приравниваются нулю (закорачиваются) и в цепи от этих источников остаются только их внутренние сопротивления (если они заданы).
В том случае, если в качестве источников энергии заданы источники тока, вместо источников тока, которые на данном этапе расчета считаются несуществующими, остаются их внутренние проводимости (цепь «несуществующих» источников разрывается).
Таким образом, метод наложения позволяет расчленить сложную задачу на ряд более простых.
Пример 9. Определить токи в ветвях цепи, изображенной на схеме рис.31
Дано: 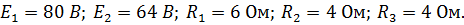
Решение: Расчет цепи произведем в два этапа.
1 этап. Пусть 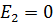 , тогда схема цепи упростится и будет иметь вид, изображенный на рис. 32.
, тогда схема цепи упростится и будет иметь вид, изображенный на рис. 32.
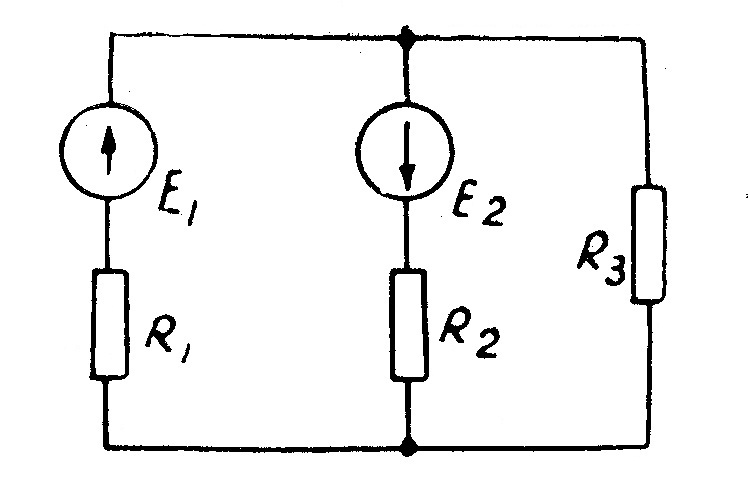 Рис. 31
Рис. 31
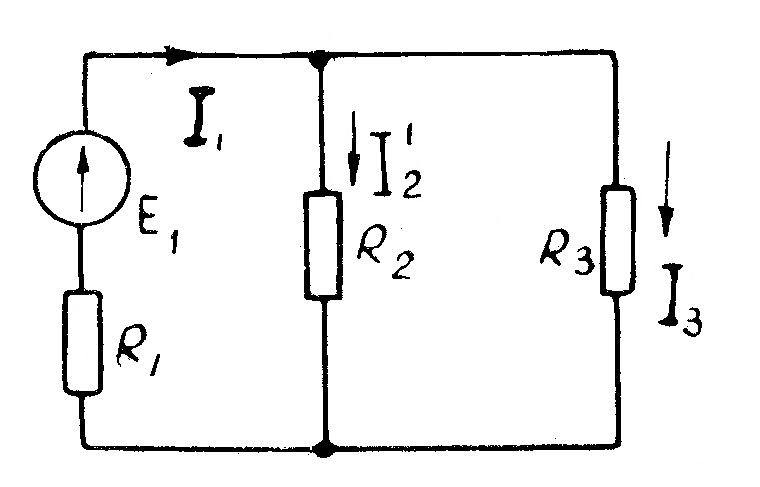
Рис. 32
Расчет такой цепи произведем по формулам закона Ома.
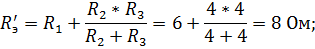
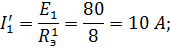
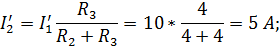
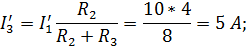
2 этап. Пусть 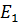 =0. В этом случае схема цепи будет иметь вид, изображенный на рис. 33.
=0. В этом случае схема цепи будет иметь вид, изображенный на рис. 33.
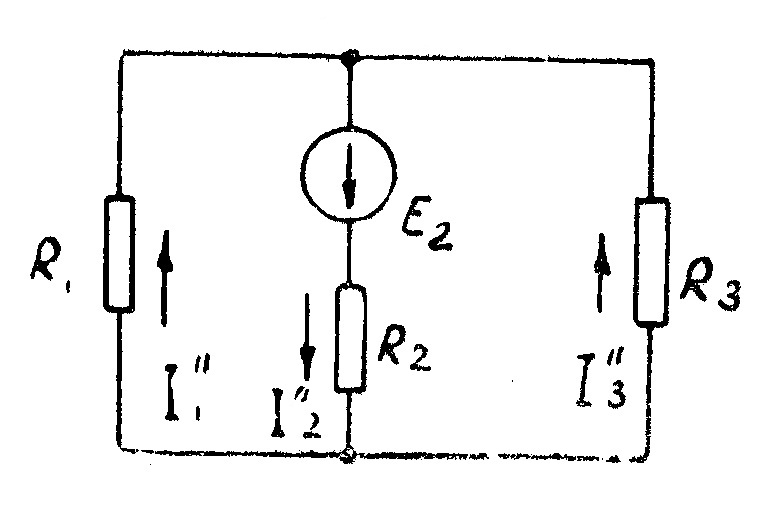
Рис. 33
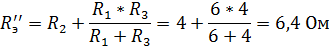
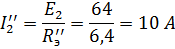
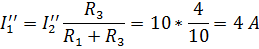
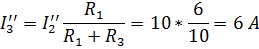
Суммарные (действительные) токи в ветвях с учетом направления частичных токов будут равны
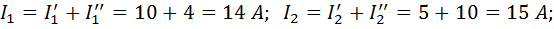
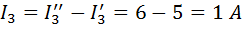
Для проверки правильности расчета составим уравнение баланса мощностей:
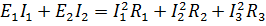
80*14+64*15= 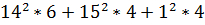
2080 = 2080
Дата добавления: 2016-04-06; просмотров: 10298;
