Метод контурных токов
При расчете цепей методом уравнений Кирхгофа приходится решать громоздкие системы уравнений. Расчет значительно упростится, если из системы уравнений исключить уравнения, составленные по первому закону Кирхгофа. С этой целью вводятся, так называемые контурные токи, т.е. токи, замыкающиеся в независимых контурах. Составление уравнений производится по формулам общего вида, что также облегчает расчет цепей. Вывод уравнений общего вида сделаем на основании второго закона Кирхгофа. Пусть дана сложная электрическая цепь (рис. 26). Зададим на правления токов в ветвях. Выберем независимые контуры (в данной схеме таких контуров три) и произвольно зададим направления контурных токов ( 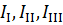 )
)
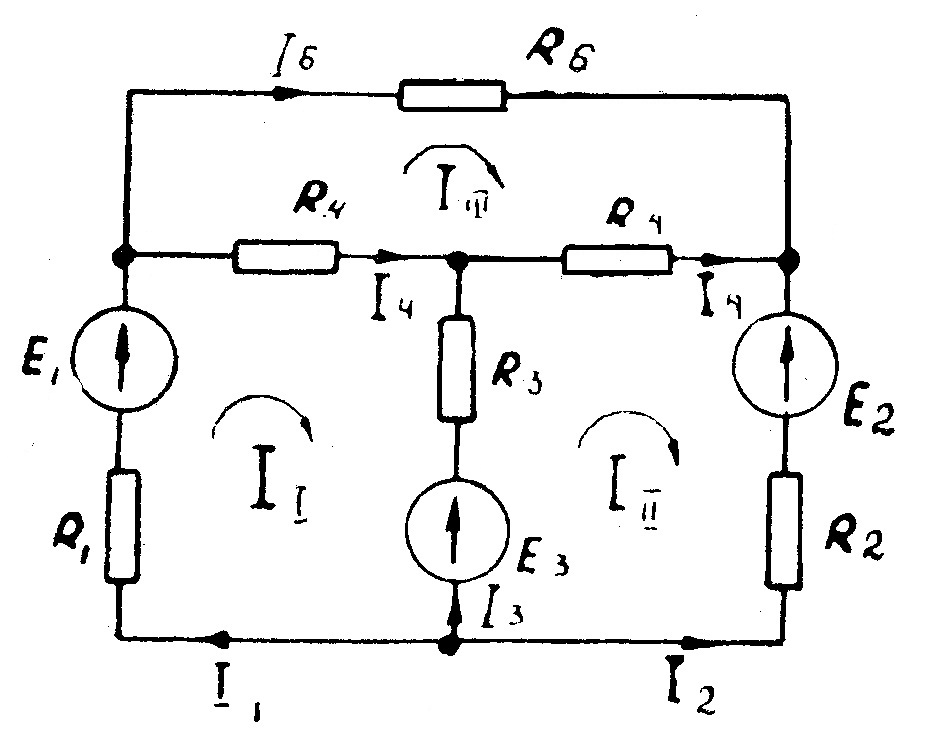
Рис. 26
Между контурными и действительными токами в ветвях существует зависимость
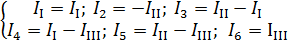 2.14
2.14
Составим уравнения по второму закону Кирхгофа для выбранных контуров, обходя их по направлению контурных токов. Количество таких уравнений равно [Р—(q-1)]
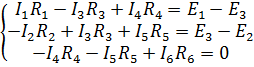
Вместо действительных токов поставим в уравнения контурные токи:
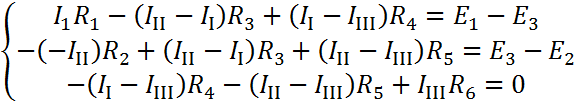
Раскроем скобки и сгруппируем члены с одинаковыми неизвестными:
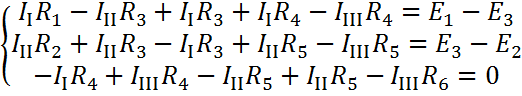
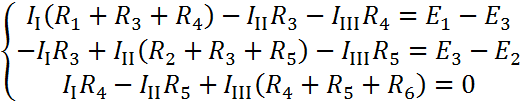
Введем дополнительные обозначения:
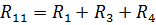 — собственное сопротивление первого контура, равное сумме сопротивлений, входящих в 1-й контур;
— собственное сопротивление первого контура, равное сумме сопротивлений, входящих в 1-й контур;
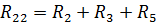 — собственное сопротивление второго контура, равное сумме сопротивлении, входящих во 2-й контур;
— собственное сопротивление второго контура, равное сумме сопротивлении, входящих во 2-й контур;
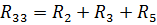 — собственное сопротивление третьего контура, равное сумме сопротивлений, входящих в 3-й контур;
— собственное сопротивление третьего контура, равное сумме сопротивлений, входящих в 3-й контур;
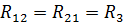 — взаимное (общее) сопротивление 1-го и 2-го контуров;
— взаимное (общее) сопротивление 1-го и 2-го контуров;
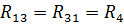 — взаимное (общее) сопротивление 1-го и 3-го контуров;
— взаимное (общее) сопротивление 1-го и 3-го контуров;
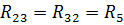 —взаимное (общее) сопротивление 2-го и 3-го контуров;
—взаимное (общее) сопротивление 2-го и 3-го контуров;
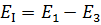 — контурная э.д.с. первого контура;
— контурная э.д.с. первого контура;
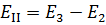 —контурная э.д.с. второго контура.
—контурная э.д.с. второго контура.
С учетом принятых обозначений система уравнений примет вид:
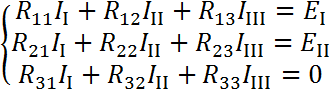 (2.15)
(2.15)
Уравнения (2.15) представляют собой формулу общего вида. При составлении уравнений по формулам общего вида необходимо соблюдать следующие правила:
а) Если направления контурных токов во всех контурах выбрать одинаковыми, то все взаимные сопротивления следует брать со знаком минус;
б) при вычислении контурных э.д.с. со знаком плюс следует брать те э.д.с., направления которых совпадают с направлениями контурного тока в рассматриваемом контуре, остальные э.д.с. следует брать со знаком минус.
В результате решения системы уравнений (2.15) находим значения контурных токов. Действительные токи определятся как алгебраическая сумма контурных токов, действующих в данной ветви, по формулам 2. 14. Направления действительных токов в ветвях будут соответствовать направлениям больших контурных токов.
Расчет цепей методом контурных токов производится в следующем порядке:
а) Выбирают [Р-(q-1)] независимых контуров и произвольно задаются направлениями контурных токов;
б) составляют систему уравнений по формулам общего вида (2.15);
в) вычисляют взаимные и собственные сопротивления контуров и контурные э.д.с. Полученные величины подставляют в уравнения;
г) решают систему уравнений и уточняют направления контурных токов (если какой-либо контурный ток получится со знаком минус, то направление этого контурного тока следует считать противоположным заданному);
д) определяют действительные токи в ветвях по формулам (2.14)
Пример 6. Используя данные примера 5, произвести расчет цепи (схема цепи рис. 25) методом контурных токов.
Решение: Выбираем два независимых контура abcd и bcfe. Зададимся направлением контурных токов. Пусть ток 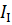 в контуре abcd направлен по ходу часовой стрелки, а ток
в контуре abcd направлен по ходу часовой стрелки, а ток 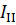 в контуре bсfе – против хода часовой стрелки.
в контуре bсfе – против хода часовой стрелки.
Так как независимых контуров в данной цепи 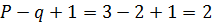 , то необходимо составить два уравнения по формулам общего вида
, то необходимо составить два уравнения по формулам общего вида
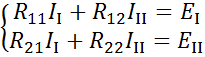
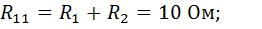
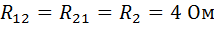
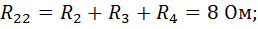
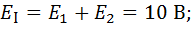
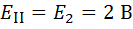
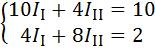
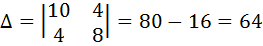
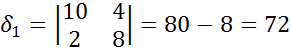
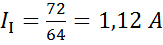
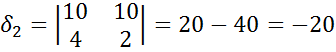
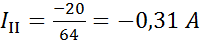
Контурный ток 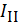 получился со знаком минус, это значит, что его направление нужно считать по ходу часовой стрелки. Действительные токи в ветвях:
получился со знаком минус, это значит, что его направление нужно считать по ходу часовой стрелки. Действительные токи в ветвях:
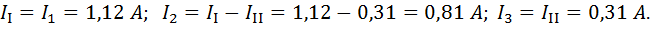
Дата добавления: 2016-04-06; просмотров: 2796;
