Метод пропорциональных величин (метод подобия)

Применение этого метода основывается на том, что в линейной цепи с одним источником питания имеет место линейная зависимость между напряжением на входе схемы и токами ее отдельных ветвей. Вследствие этого изменение напряжения на входе цепи в k вызывает изменение токов в ветвях также в k раз.

На примере расчета цепи (рис. 21) рассмотрим последовательность определения токов. Задаемся произвольным значением тока в наиболее удаленной от источника ветви, в данном случае значением тока в пятой ветви .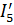

По известному сопротивлению 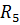и заданному значению тока 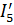вычисляем напряжение между точками dc: .

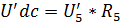Тогда ток в четвертой ветви будет равен: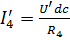

Согласно первому закону Кирхгофа ток в третьей ветви: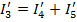

Напряжение между точками а и Ь равно сумме падений напряжений на участках сd и сb: 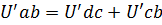, где

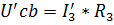
Далее определяем токи 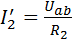и

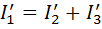
Напряжение на входе цепи равно сумме падений напряжений на участке аb и на сопротивлении : .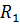

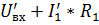Найденное напряжение на входе цепи отличается от действительного. Находим коэффициент пропорциональности k.

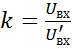или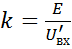

Для определения действительных токов в ветвях необходимо все вычисленные и произвольно заданные значения токов ( 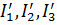и т. д.) умножить на коэффициент пропорциональности k.