Метод уравнений Кирхгофа
Метод уравнений Кирхгофа является классическим методом. Все остальные методы расчета сложных цепей в той или иной степени основаны на применении законов Кирхгофа. Рассмотрим расчет цепи с помощью уравнений Кирхгофа, если заданы все э.д.с. и сопротивления приемников электрической энергии. Число неизвестных токов равно количеству ветвей в заданной цепи (Р). Поэтому для нахождения токов необходимо составить систему Р—уравнений с Р—неизвестными.
Если цепь имеет q—узлов, то по первому закону Кирхгофа можно составить уравнение. Однако число независимых уравнений будет на единицу меньше, т.е. по первому закону Кирхгофа независимых уравнений можно составить (q-1). Остальные уравнения, число которых равно n=[Р-(q-1)], составляют по второму закону Кирхгофа, порядком изложенным в § 3.
Таким образом, расчёт сложных цепей методом уравнений Кирхгофа можно подразделить на следующие этапы:
а) подсчитать число ветвей Р и число узлов q;
б) произвольно задать направления токов в ветвях и обозначить их стрелками на схеме;
в) выбрать [Р-(q-1)] независимых контуров (с этой целью удобно выбирать простые контуры, т.е. контуры не имеющие внутренних ветвей) и произвольно задать направления обхода контуров;
г) составить (q-1) уравнений по первому закону Кирхгофа и [Р-(q-1)] уравнений по второму закону Кирхгофа для выбранных контуров;
д) решить систему уравнений.
Если в результате расчета токи в каких-либо ветвях получатся со знаком минус, то это означает, что в действительности в этих ветвях токи текут в направлении, противоположном произвольно заданным.
Для проверки правильности расчета составить уравнение баланса мощностей (1.17).
Пример 5. Определить токи в ветвях цепи, изображенной на рис. 25.
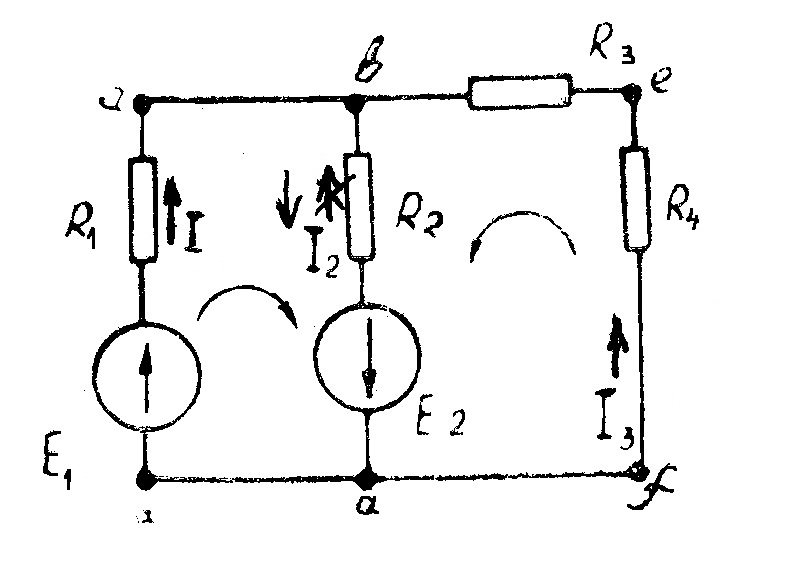
Рис. 25
Дано: 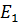 =8 B;
=8 B; 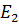 ==2 B;
==2 B; 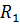 = =6 Oм;
= =6 Oм; 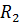 ==4 Oм;
==4 Oм; 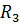 ==3Oм;
==3Oм; 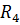 ==1 Ом.
==1 Ом.
Решение. Заданная цепь состоит из 3-x ветвей (Р=3) и двух узлов (q=2). Необходимо составить три уравнения, из них одно уравнение по первому и два уравнения по второму законам Кирхгофа. Произвольно выбранные направления токов в ветвях и направления обхода контуров показаны на схеме стрелками.
Составим уравнения:
—по первому закон у Кирхгофа: 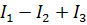 =0;
=0;
—по второму закону Кирхгофа для контура ad cb: 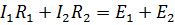
для контура bc fс: 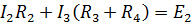
Таким образом, имеем систему уравнений:
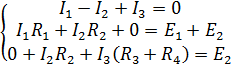
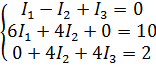
Вычислим определители и найдем точки в ветвях:
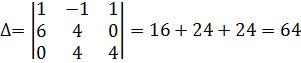
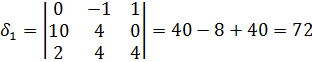
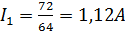
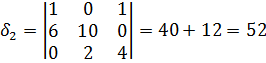
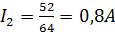
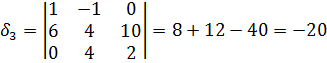
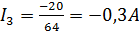
Знак минус для тока 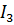 означает, что направление тока в третьей ветви противоположно выбранному (на рис. 25 действительное направление тока
означает, что направление тока в третьей ветви противоположно выбранному (на рис. 25 действительное направление тока 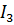 показано пунктирной стрелкой) для проверки правильности расчета составим уравнение баланса мощностей
показано пунктирной стрелкой) для проверки правильности расчета составим уравнение баланса мощностей
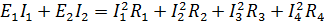
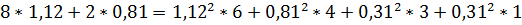
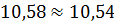
Дата добавления: 2016-04-06; просмотров: 2540;
