Критерий идеального наблюдателя
(критерий Котельникова)
Этот критерий требует обеспечения минимума средней вероятности ошибочного приема.
Для двоичной системы
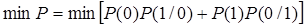 ,
,
для m-ичной системы
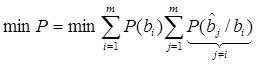 ,
,
где
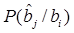 – условная вероятность j-ой ошибки при передаче
– условная вероятность j-ой ошибки при передаче
i-го сообщения,
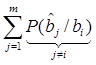 – условная вероятность любой ошибки при передаче
– условная вероятность любой ошибки при передаче
i-го сообщения,
Р – безусловная вероятность любой ошибки.
Вычислим условную вероятность конкретной ошибки
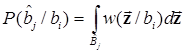 ,
,
где 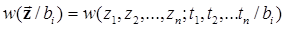 – n-мерная условная плотность вероятности (при разложении
– n-мерная условная плотность вероятности (при разложении 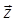 в n-мерном евклидовом пространстве по любому базису), а интеграл, вычисляемый по векторной переменной
в n-мерном евклидовом пространстве по любому базису), а интеграл, вычисляемый по векторной переменной 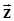 , очевидно, n-кратный. Таким образом, критерий Котельникова приобретает вид
, очевидно, n-кратный. Таким образом, критерий Котельникова приобретает вид
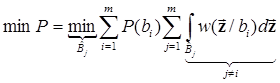 , (6.1)
, (6.1)
где 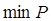 находится варьированием областей
находится варьированием областей 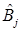 .
.
Минимуму средней вероятности ошибок соответствует максимум средней вероятности правильного приема (иная эквивалентная форма записи критерия Котельникова)
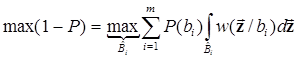 . (6.2)
. (6.2)
Учитывая, что демодулятор должен реализовать критерий (6.1) или (6.2), принимая решение 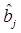 на основе анализа единственной реализации
на основе анализа единственной реализации 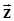 на интервале 0 – Т, рассмотрим апостериорную вероятность вида
на интервале 0 – Т, рассмотрим апостериорную вероятность вида 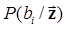 , т.е. вероятность того, что при приеме сигнала
, т.е. вероятность того, что при приеме сигнала 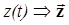 передавалось сообщение bi . Очевидно, что максимум средней вероятности правильного приема будет достигнут, если всякую реализацию принятого колебания z(t) относить к той области
передавалось сообщение bi . Очевидно, что максимум средней вероятности правильного приема будет достигнут, если всякую реализацию принятого колебания z(t) относить к той области 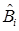 , для которой апостериорная вероятность
, для которой апостериорная вероятность 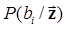 максимальна, т.е. решение в пользу
максимальна, т.е. решение в пользу 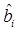 принимается при совместном выполнении совокупности неравенств
принимается при совместном выполнении совокупности неравенств
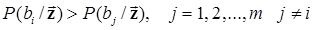 .
.
Иначе говоря, критерий Котельникова требует максимизации апостериорной (обратной) вероятности и его можно записать в виде
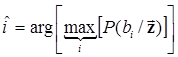 . (6.3)
. (6.3)
Для выполнения анализа (6.3) воспользуемся известной формулой Байеса
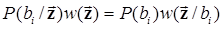 .
.
Тогда
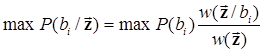 ,
,
а выражение (6.3) принимает вид
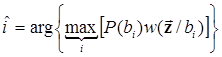 (6.4)
(6.4)
(безусловная плотность вероятности 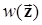 здесь исключена, т. к. она не зависит от i и, следовательно, не влияет на решение).
здесь исключена, т. к. она не зависит от i и, следовательно, не влияет на решение).
В развернутом виде критерий (6.4) можно записать в виде системы из m-1 неравенств
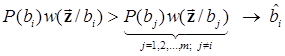 ,
,
или
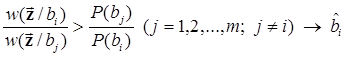 .
.
Условную плотность вероятности 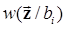 , рассматриваемую при известном после приема векторе
, рассматриваемую при известном после приема векторе 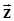 как функцию аргумента bi, называют функцией правдоподобия гипотезы о передаче сообщения bi, а
как функцию аргумента bi, называют функцией правдоподобия гипотезы о передаче сообщения bi, а 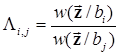 - отношением правдоподобия двух гипотез о передаче сообщений bi и bj. С учетом этого критерий Котельникова можно записать в виде:
- отношением правдоподобия двух гипотез о передаче сообщений bi и bj. С учетом этого критерий Котельникова можно записать в виде:
если 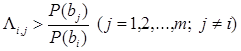 , то решение
, то решение 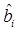 . (6.5)
. (6.5)
Рассмотренный критерий Котельникова обладает следующими особенностями:
1) требует знания априорных безусловных вероятностей отдельных сообщений  ;
;
2) безразличен к виду ошибок 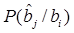 (все виды ошибок одинаково нежелательны), что приводит к росту ошибок при приеме менее вероятных сообщений, а они являются более информативными.
(все виды ошибок одинаково нежелательны), что приводит к росту ошибок при приеме менее вероятных сообщений, а они являются более информативными.
Дата добавления: 2016-04-02; просмотров: 2269;
