Синтез оптимального демодулятора при
Известном ансамбле сигналов (когерентный прием)
Постановка и решение задачи когерентного приема
На корреляторах
Постановка задачи:
Известны:
1. Ансамбль сигналов на выходе модулятора
{si(t)}; i = 1, 2,…, m; t Î (0, T).
2. Непрерывный канал
,
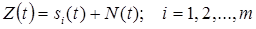где N(t) – квазибелый нормальный шум, т. е.
.
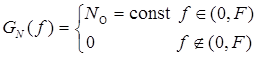3. В качестве критерия качества приема задан критерий максимального правдоподобия (6.6)
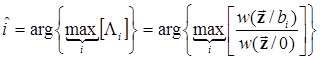
Требуетсясинтезировать оптимальный демодулятор, иначе говоря, найти алгоритм оптимальной обработки входного сигнала и принятия решения о передаваемом сообщении.
Решение
В основу решения положим выражение заданного критерия качества приема, для чего рассмотрим входящие в него функции правдоподобия гипотез:
1) о наличии во входном колебании z(t) i-го сигнала [z(t) = si(t) + n(t)]
,
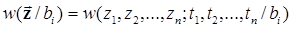2) об отсутствии в нем какого-либо сигнала [z(t) = n(t)]
,
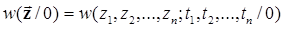где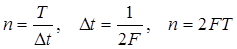 
.
Начнем с последней. Учитывая, что сечения квазибелого шума, разделенные интервалами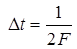 
, не коррелированны, а в силу нормального распределения шума и независимы, получим
.
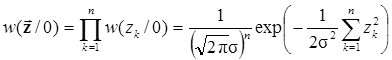Поскольку СП Z(t) = si(t)+ N(t) отличается от шума N(t) только известным, а потому неслучайным сигналом si(t), играющим роль математического ожидания Z(t), то
,
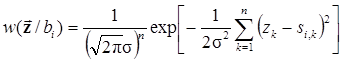где использовано обозначение si,k = si(tk).
В итоге отношение правдоподобия гипотез о наличии и отсутствии сигнала принимает вид
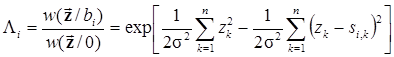
или с учетом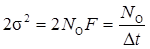 
.
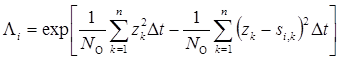Перейдем к белому шуму, сняв ограничение на ширину его спектра (F ® ¥). Иначе говоря, от евклидова пространства перейдем к гильбертовому. При этом
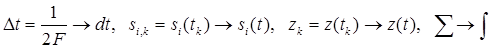
и
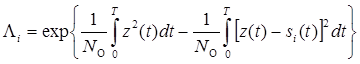. (6.10)
Синтезируемый демодулятор должен принимать решение в пользу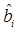 
, обеспечивающего максимум выражения (6.10), или, что эквивалентно, максимум показателя экспоненты в нем
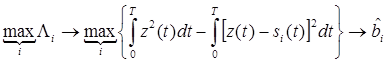. (6.11)
Нетрудно видеть, что максимум (6.11) достигается при минимуме вычитаемого
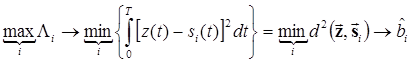. (6.12)
Демодулятор оптимальный по критерию максимального правдоподобия принимает решение в пользу того символа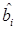 
, сигнал si(t) которого отстоит от принятого колебания z(t) на меньшее расстояние.
 |
Рассматривая выражение (6.12) как алгоритм обработки принятого колебания z(t) приходим к схеме демодулятора, представленной на рис. 6.2.
Другую форму алгоритма можно получить из выражения (6.11)
,
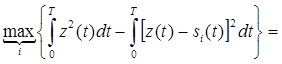
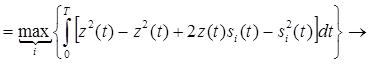
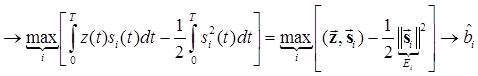или
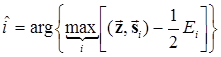, (6.13)
где Ei – энергия i-го сигнала.
 |
Схема оптимального демодулятора, реализующего алгоритм (6.13), приведена на рис. 6.3. Поскольку в каждой ветви такого демодулятора присутствует вычислитель скалярного произведения
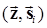– коррелятор, то его называют демодулятором на корреляторах (активных фильтрах).
 |
Если использовать сигналы равных энергий, то алгоритм (6.13) и схема демодулятора (рис. 6.3) существенно упрощаются (рис. 6.4)
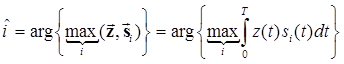. (6.14)
Все вышерассмотренные демодуляторы используют всю информацию о форме сигналов si(t), включая начальную фазу. В каждой их ветви содержатся генераторы, генерирующие синфазные образцы этих сигналов, поэтому их называют когерентными демодуляторами.
Дата добавления: 2016-04-02; просмотров: 1227;