Фазо-частотная характеристика СФ

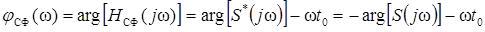
отличается знаком от фазового спектра сигнала, с которым он согласован (без учета слагаемого –ωt₀).

3. Форма отклика СФ на «свой» сигнал (сигнал с которым он согласован)

.

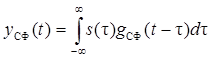Учитывая, что из (6.15) вытекает 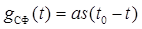, получим

.

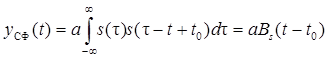Таким образом, отклик СФ на «свой» сигнал с точностью до коэффициента совпадает с его корреляционной функцией, смещенной по оси времени на интервал t₀ (рис. 6.7)

.

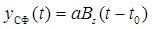Из полученного результата вытекают следующие выводы:

· Отклик СФ на «свой» сигнал с точностью до постоянного коэффициента совпадает с его корреляционной функцией.

· Длительность отклика на «свой» сигнал всегда равна 2Т.

· СФ не восстанавливает форму сигнала, искаженного шумом. Его задача создать один отсчет y(t₀), по которому можно наилучшим образом судить о присутствии на входе «своего» сигнала.

4. СФ обеспечивает наибольшее отношение сигнал/шум (с/ш) на своем выходе при действии на входе аддитивной смеси «своего» сигнала и центрированного нормального белого шума 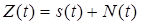со спектральной плотностью мощности N=N_О/2.

Докажем это, уточнив предварительно, что под отношением с/ш на выходе СФ понимают отношение математического ожидания отсчета случайной реакции СФ Y(t) в момент времени t₀ = T к корню из ее дисперсии

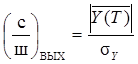. (6.16)

Рассмотрим произвольный линейный фильтр с передаточной функцией 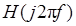. Поскольку 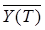представляет собой отсчет реакции y_s(T) на математическое ожидание воздействия, каковым является сигнал s(t), то

.

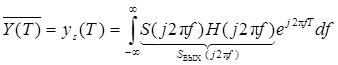Полученное выражение представляет собой не что иное, как скалярное произведение 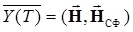двух векторов 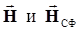в комплексном пространстве Гильберта, если иметь в виду следующие соответствия:

.

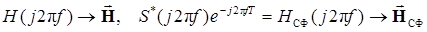Вычислим дисперсию случайной величины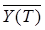

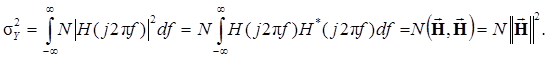Подставляя полученные результаты в выражение (6.16) и применяя неравенство Коши-Буняковского-Шварца

,

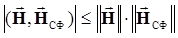имеем

.

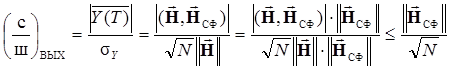Наибольшее значение с/ш (равенство в полученном выражении) достигается при совпадении векторов 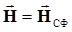, т. е. для случая использования СФ, что и требовалось доказать. Это чрезвычайно важное свойство некоторые авторы закладывают в основу определения СФ.

Найдем саму величину отношения с/ш на выходе СФ при действии на его входе «своего» сигнала

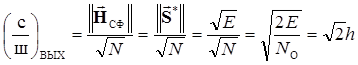, (6.17)

где Е – энергия «своего» сигнала,

N_О – односторонняя спектральная плотность мощности шума,

.

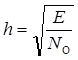Таким образом, максимальное отношение с/ш на выходе СФ определяется энергией «своего» сигнала, независимо от его формы.

Определим отношение с/ш по мощности

,

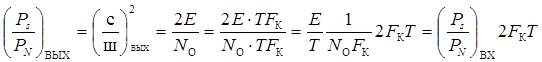где F_K – ширина полосы пропускания канала.

При совпадении ширины полосы пропускания канала с шириной спектра сигнала F_K = F_s имеем

.

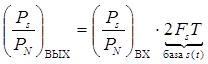Отсюда вытекает целесообразность выбора сигналов с большой базой 2F_sT для передачи дискретных сообщений, что позволяет увеличить отношение с/ш при согласованной фильтрации.