Расчеты отклонений формы и расположения обработанных поверхностей, вызванных деформациями
Упругие деформации колец при закреплении в СП значительно снижают точность обработки, особенно если кольца тонкостенные (отношение толщины стенки к среднему радиусу h/r < 0,2).
Патроны кулачковые, мембранные, оправки и патроны самозажимные, цанговые, оправки кулачковые развивают асимметричные, т. е. неравномерные по окружности, силы закрепления. Приспособления магнитные, гидропластмассовые, с гофрированными втулками, с резиновыми кольцами, с шайбами упругими разжимными, оправки цилиндрические и прессовые развивают осесимметричные, т. е. равномерные по окружности, силы закрепления.
В общем случае под действием сил закрепления поперечные сечения кольца получают радиальные и угловые перемещения, которые могут вызвать отклонения размеров, соизмеримые с допусками 1 – 4 - го квалитета, а также отклонения формы и расположения.
При обработке тонкостенных колец и гильз меньшее отклонение от круглости обеспечивают приспособления с осесимметричными силами закрепления.
Методика расчета деформаций тонкостенных колец при закреплении радиальными силами применима при отношении толщины стенки кольца к среднему радиусу h/r ≤ 0,2 и при условии, что кольцо полностью перекрыто кулачками или длина участков кольца, выступающих за кулачки, не превышает
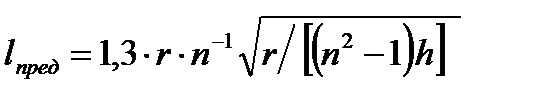
где n – число кулачков; r и h – средний радиус и толщина стенки кольца соответственно, мм (рис. 5).
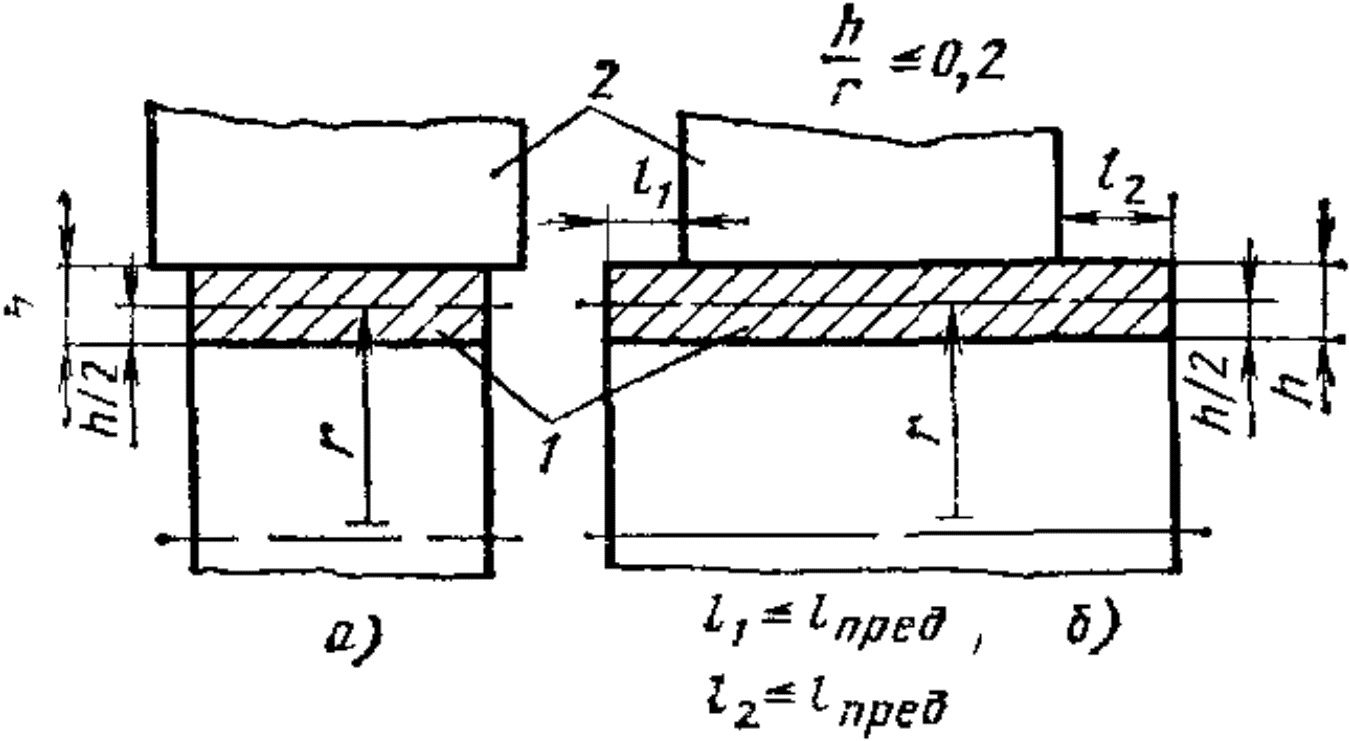
|
| Рис. 5. Положения тонкостенного кольца 1 в кулачках 2: а – кольцо полностью перекрыто кулачками, б – длина участков l1 и 12 кольца, выступающих за кулачки, не превышает lпред |
На рис. 6 представлена номограмма, позволяющая быстро найти lпред. при известных n, r и h/r. Отношение lпред/r определяется как ордината точки пересечения вертикали h/r с прямой, соответствующей числу кулачков n (например, при h/r = 0,18 и числе кулачков n = 3 lпред/r =0,36).

|
| Рис 6. Номограмма для определения lпред |
При n > 12 и осесимметричном скреплении (n = ∞), а также если точка пересечения находится в области, расположенной ниже прямой аb где прямые показаны штрихами), величина lпред определяется по ординате точки пересечения вертикали h/r с прямой аb.
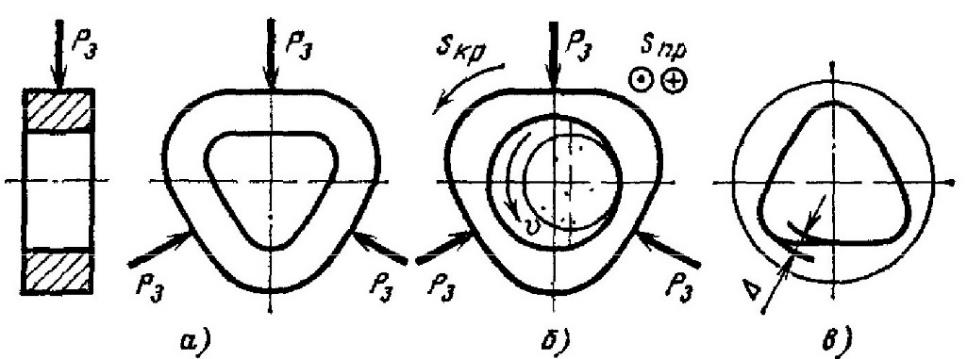
Схемы возникновения погрешностей обработки в связи с деформацией кольца при закреплении показаны на рис. 7 и 8. Тонкостенное кольцо было закреплено тремя радиальными силами Рз, проходящими через центры тяжести его поперечных сечений, и сформировалось (рис. 7, а). В закрепленном состоянии кольцо шлифуют по отверстию, которое получает цилиндрическую форму (рис. 7, б). После обработки кольцо, снятое с
|
| Рис. 7. Схема возникновения отклонения от кругл ости тонкостенного кольца из-за деформаций при закреплении радиальными силами, проходящими через центры тяжести его поперечных сечений; а – кольцо закреплено, по еще не обрабатывается; б – кольцо шлифуют по внутреннем диаметру; в – обработанное кольцо снято с приспособления |
приспособления, упруго восстановилось. Обработанное отверстие приобрело трехгранную форму с отклонением от круглости ∆ (рис. 7, в).

|
| Рис. 8. Схема возникновения погрешностей обработки тонкостенного кольца из-за деформаций при закреплении кольцевой силой, не проходящей через центры тяжести его поперечных сечений: а – кольцо закреплено, по еще не обрабатывается, б – кольцо обработано, но еще закреплено; в – кольцо, снятое с приспособления, упруго восстановилось |
На рис. 8 показана схема закрепления тонкостенного кольца кольцевой силой q, не проходящей через центры тяжести его поперечных сечений. Под действием кольцевой силы q все поперечные сечения кольца повернулись на некоторый угол v. В клетку заштрихован припуск на обработку (рис. 8, а). Кольцо обработало по наружной поверхности и; правому торцу, но еще не снято с приспособления (рис. 8, б). Снятое с приспособления кольцо упруго восстановилось, в результате чего возникли конусообразность наружной поверхности с углом в v и полное торцовое биение ∆т (рис. 8, в).
В частном случае, когда радиальные силы закрепления Р3 расположены в плоскости, проходящей через центры тяжести поперечных сечений кольца (см. рис. 7), а также при длинных кулачках, исключающих возможность поворота поперечных сечений, отклонение от круглости
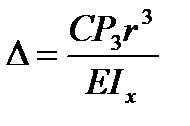
где: С – коэффициент, зависящий от числа кулачков (табл. 25); Р3 – сила закрепления на кулачке, Н; r – средний радиус кольца, мм; lx – момент инерции поперечного cечения кольца, мм4; Е – модуль упругости материала кольца; для стали Е, МПа.
| Число кулачков «n» | С | Число кулачков «n» | С |
| 0,14 | 0,0013 | ||
| 0,03 | 0,001 | ||
| 0,01 | 0,0007 | ||
| 0,006 | 0,0005 | ||
| 0,003 | 0,0004 | ||
| 0,002 |
Формула (1) справедлива при направлении сил закрепления Ра к центру и от центра кольца.
Не рекомендуется принимать число кулачков п больше двенадцати, так как отклонения от круглостиснижаются незначительно, а конструкция СП усложняется.
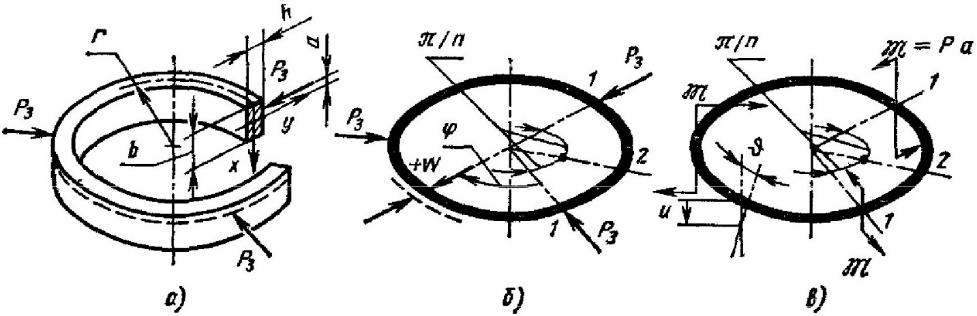
В общем случае, когда радиальные силы закрепления Р3 не проходят через центры тяжести поперечных сечений, наряду с линейными возникают угловые v и осевые u перемещения сечения кольца (рис. 9). Эти перемещения переменные по угловой координате и достигают наибольшей величины в местах приложения сил Р3, а также посередине между ними (табл. 26).
В этом случае возникают отклонение от кругл ости ∆ и торцевое биение ∆т
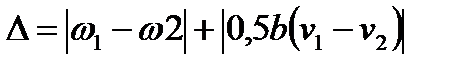
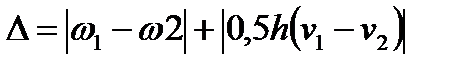
|
| Рис. 9. Схема деформаций тонкостенного кольца под действием радиальных сил, не проходящих через центры тяжести поперечных сечений кольца: а – схема закрепления кольца; б – схема определения радиальных перемещений ω кольца; в – схема определения угловых v и осевых u перемещений сечений кольца |
Формулы, приведенные в табл. 26, можно использовать также для определения перемещений сечений колец, имеющих непрямоугольное поперечное сечение, при условии, что одна из главных центральных осей поперечного сечения лежит в плоскости оси вращения кольца или составляет с этой плоскостью малый угол.
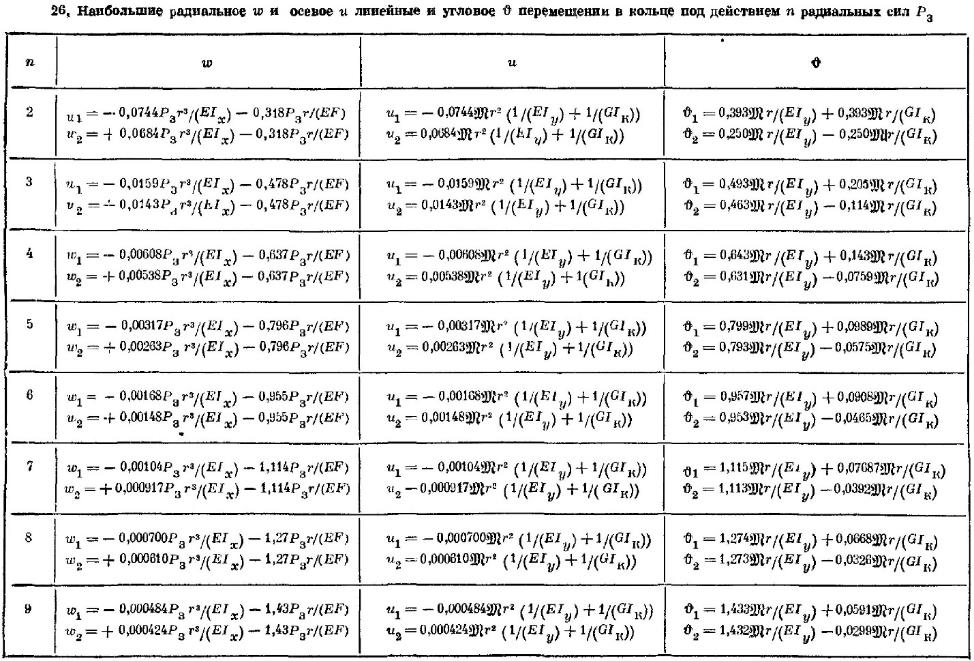

В табл. 27 приведены безразмерные коэффициенты жесткости па изгиб и кручение для колец с прямоугольным поперечным сечением при различных отношениях ширины к толщине сечения b/h.
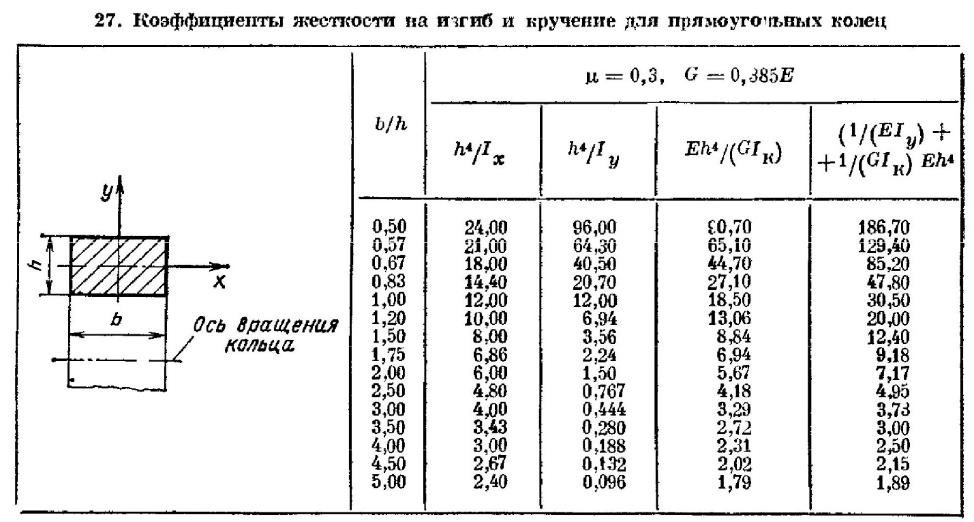
Геометрические характеристики некоторых часто встречающихся поперечных сечений колец приведены в табл. 28.


Дата добавления: 2016-02-16; просмотров: 2889;
