Принятие решений при многих критериях
Если исходы оценивают по 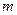 критериям
критериям 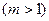 , то такая задача принятия решений называется многокритериальной. В таких задачах проявляется эффект несравнимости исходов. Если исходы сравниваются по двум критериям
, то такая задача принятия решений называется многокритериальной. В таких задачах проявляется эффект несравнимости исходов. Если исходы сравниваются по двум критериям 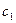 и
и 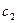 , и имеет место соотношение
, и имеет место соотношение 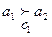 , но
, но 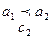 , то
, то 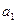 и
и 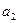 несравнимы по предпочтениям.
несравнимы по предпочтениям.
Математическая модель ЗПР при многих критериях можно представить в виде 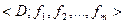 , где
, где 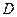 – некоторое множество допустимых исходов, а
– некоторое множество допустимых исходов, а 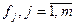 – функция, заданная на множестве
– функция, заданная на множестве 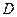 , при этом
, при этом 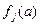 – оценка исхода
– оценка исхода 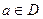 по критерию
по критерию 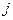 .
.
Критерий 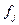 называется позитивным, если ЛПР стремится к увеличению этого критерия и негативным в противном случае. Характер критерия в конкретной задаче устанавливается исходя из ее сути.
называется позитивным, если ЛПР стремится к увеличению этого критерия и негативным в противном случае. Характер критерия в конкретной задаче устанавливается исходя из ее сути.
Пусть 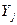 – множество значений функции
– множество значений функции 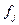 на
на 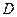 , то есть множество значений по
, то есть множество значений по 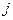 -му критерию
-му критерию 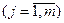 . Тогда множество
. Тогда множество 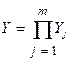 , состоящее из всевозможных упорядоченных наборов оценок по критериям
, состоящее из всевозможных упорядоченных наборов оценок по критериям 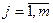 , называется множеством векторных оценок. Любой элемент
, называется множеством векторных оценок. Любой элемент 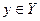 представляет собой вектор
представляет собой вектор 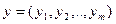 значений оценок
значений оценок 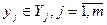 по всем критериям. Для всякого исхода
по всем критериям. Для всякого исхода 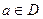 набор его оценок по всем критериям
набор его оценок по всем критериям 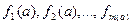 есть вектор оценок исхода
есть вектор оценок исхода  . Таким образом, сравнение исходов заменяется сравнением их векторных оценок.
. Таким образом, сравнение исходов заменяется сравнением их векторных оценок.
Основное отношение, по которому производится сравнение векторных оценок – доминирование по Парето. Исход 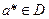 называется Парето-оптимальным исходом в
называется Парето-оптимальным исходом в 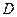 , если он не доминируется никаким другим исходом из
, если он не доминируется никаким другим исходом из 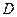 . Парето-оптимальность исхода
. Парето-оптимальность исхода 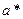 означает, что он не может быть улучшен ни по одному критерию без ухудшения по какому-либо другому критерию.
означает, что он не может быть улучшен ни по одному критерию без ухудшения по какому-либо другому критерию.
Проблема оптимальности для многокритериальных ЗПР заключается в том, что сформулировать единый принцип оптимальности для таких задач нельзя, так как понятие векторного оптимума не определено. Кандидатом на оптимальное решение в многокритериальных ЗПР может быть только Парето-оптимальное решение. Это необходимое условие оптимальности, однако таких исходов, как правило, бывает несколько 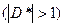 , и любые 2 из них несравнимы по Парето. Если нет информации об относительной важности критериев, то рациональный выбор между Парето-оптимальными исходами сделать невозможно.
, и любые 2 из них несравнимы по Парето. Если нет информации об относительной важности критериев, то рациональный выбор между Парето-оптимальными исходами сделать невозможно.
Возможно 2 подхода:
1. Для заданной ЗПР отыскивается множество Парето-оптимальных исходов, а выбор конкретного оптимального исхода предоставляется сделать ЛПР (из этого множества).
2. Производится сужение множества Парето-оптимальных исходов (в идеале до 1 элемента) с помощью некоторых формализованных процедур, но для этого требуется дополнительная информация о критериях или о свойствах оптимального решения.

Дата добавления: 2016-03-20; просмотров: 783;
