На основе математического моделирования. Этап 1. Построение математической модели ЗПР.

Этап 1. Построение математической модели ЗПР.

Определяются 3 множества: множество допустимых альтернатив (управляющих воздействий) 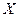, причем 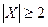; множество возможных состояний среды 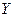; множество возможных исходов (состояний управляемой системы) .

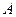Существует функция 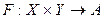, функция реализации. Набор объектов 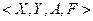составляет реализационную структуру ЗПР. Еще один компонент ЗПР называется оценочной структурой, которая может задаваться разными способами:

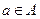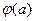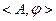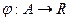1) если ЛПР может оценить эффективность (полезность, значимость, важность, целесообразность и т. д.) каждого исхода некоторым числом , то оценочная структура задается в виде пары , где – оценочная функция.

2) указание отношения предпочтения исходов, что сводится к перечислению пар исходов 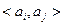таких, для которых 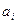лучше : .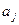

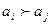
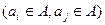Оценочная структура имеет субъективный характер, так как оценивание исходов производится с точки зрения ЛПР.

Целевая функция: 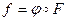, то есть 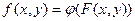, 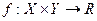. Целевая функция имеет следующий содержательный смысл: число 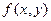есть оценка полезности (с точки зрения ЛПР) того исхода, который возникает в ситуации, когда ЛПР выбирает альтернативу 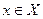, а среда находится в состоянии .

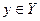В некоторых ЗПР оценка исхода характеризует его в негативном смысле, являясь выражением затрат, убытков, ущерба и т. д. В этом случае целевая функция называется функцией потерь.

Этап 2. Формулирование принципа оптимальности и нахождение оптимального решения.

Универсального понятия оптимального решения, которое было бы пригодно для любой ЗПР, не существует. Задача нахождения оптимального решения (в смысле некоторого указанного принципа оптимальности) является уже формальной задачей и решается математическими средствами. Для ЗПР данного класса может существовать не один, а несколько различных принципов оптимальности. Кроме того, при фиксированном принципе оптимальности может быть не одно, а несколько оптимальных решений.

Этап 3. Анализ полученных результатов.

Такой анализ проводится на содержательном уровне и заключается в соотнесении формально полученных рекомендаций с требованиями конкретной задачи. Если полученные формальным способом оптимальные решения по каким-либо причинам оказываются неприменимыми, то делают следующее:

1) выбирают другое оптимальное решение (если оно имеется)

2) выбирают другой принцип оптимальности

3) изменяют саму математическую модель ЗПР