Эффективная ставка операции

В случае, когда финансовая операция предполагает последовательность перемежающихся поступлений денег и выплат, ее удобно описывать двусторонним потоком платежей.

Удобно поток платежей представить в виде графической схемы (см. рис. 3.8.).

Рис. 3.8.

При этом поступлениям денег в моменты t₁, t₃, t₄, ¼ t_n-1 соответствуют положительные величины с₁, с₃, с₄, ¼ с_n-1, а выплатам в моменты t₂, t₅, ¼ t_n соответствуют отрицательные величины с₂, с₅, ¼ с_n.

Для оценки финансовой сделки, описываемой двусторонним потоком платежей, удобно использовать:

S(0) – чистое современное значение или чистый приведенный доход, NPV (netto PV) – чистое PV;

S(t) – чистое будущее значение или чистая наращенная сумма, NFV (netto FV) – чистое FV.

Если чистый приведенный доход S(0) (NPV) больше нуля, S(0)>0 (NPV>0), то сделка выгодна. В противном случае сделка невыгодна.

Расчет чистого приведенного дохода S(0) и чистой наращенной суммы S(t) возможен по формулам (3.1)–(3.3) с учетом знаков величин c_k.

Пример 40.

Контракт между фирмой и банком предусматривает, что банк предоставляет в течение 3 лет кредит фирме ежегодными платежами в размере 1 млн $ в начале каждого года под ставку 10 % годовых. Фирма возвращает долг, выплачивая 1 млн, 2 млн и 1 млн $ последовательно в конце 3, 4-го и 5-го года.

Найти S(0) чистый приведенный доход (NPV) для банка.

Представим исходные данные в виде схемы:

Рис. 3.9.

Тогда:

.

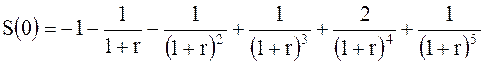Подставляя значение процентной ставки r=10%=0.1 (1/год), получим:

млн $.

В связи с тем, что S(o)>0 (NPV>0) сделка для банка является приемлемой. Из приведенных формул видно, что при росте процентной ставки r чистое современное значение NPV убывает. Если, например, процентную ставку r в 10 % чуть-чуть увеличить, то чистое современное значение V станет сначала равным нулю, а затем и отрицательным и, следовательно, инвестиционный проект будет неприемлем.

Таким образом, в экономических расчетах особую роль играет процентная ставка r, при которой чистое современное значение NPV равно нулю.

Для оценки эффективности сделки, заданной двусторонним потоком платежей, используется понятие эффективной ставки операции или внутренней эффективности (IRR, internal rate of return).

Под эффективной ставкой финансовой операции понимается значение ставки процента r, при котором чистое современное значение равно нулю, т. е. NPV( r ) = 0.

Таким образом, из (3.1) эффективная ставка является решением уравнения:

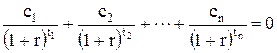(3.20)

где с₁, с₂, ¼, с_n – известные величины платежей со знаками плюс или минус, производимых в моменты t₁, t₂, ¼, t_n.

В общем случае уравнение (3.20) аналитически решить невозможно. Однако в этом случае могут быть использованы хорошо разработанные численные методы, например, метод Ньютона. Эти методы реализованы, например, в «Пакете анализа» в Excel. Название функции вычисляющей чистый внутренний доход (эффективную ставку) ЧИСТВНДОХ().

Понятие эффективной ставки операции естественно обобщает введенное ранее в п. 2.4 понятие эффективной ставки.

Пример 41.

Сравнить эффективность трех сделок:

1. В начале первого года банк дает фирме кредит в размере 3 млн руб. В конце второго года фирма возвращает 3,5 млн руб.

2. Банк дает фирме кредит в два этапа: в начале первого года – 2 млн руб., в начале второго года – 1 млн руб. В конце второго года фирма возвращает 3,5 млн руб.

3. Банк дает фирме кредит в два этапа: в начале первого года – 1 млн руб., в начале второго года – 2 млн руб. В конце второго года фирма возвращает 3,5 млн руб.

Решение.

Найдем эффективные ставки для всех трех сделок и сравним их.

Схемы двусторонних потоков для сделок приведены на рисунке.

Рис. 3.10.

Приравнивая к нулю приведенное современное значение NPV, получим уравнение для определения эффективной ставки r.

1 сделка:

, отсюда .

2 сделка:

.

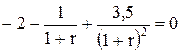Вводя обозначения x = 1+r, получим квадратное уравнение:

.

Решая его, получим: .

Тогда .

3 сделка:

.

Аналогично предыдущему, получаем уравнение для x = 1+r

.

Отсюда .

Тогда эффективная ставка сделки равна r=12,132 %.

Очевидно, что третья сделка существенно выгоднее остальных сделок.

В приведенном выше примере расчет эффективной ставки сводился к решению квадратного уравнения. В общем случае вычисление эффективной ставки r сводится к решению уравнения (3.20). Если не существует положительного решения для r, то поток платежей не выгоден. В противном случае степень выгодности потока платежей оценивается значением эффективной ставки .

Приведенные в данном разделе методы расчета универсальны и могут быть использованы как для финансовых вычислений по ценным бумагам, так и для финансового анализа производственных инвестиций и оценке эффективной ставки кредита.