Однонаправленные потоки платежей

Финансовые контракты, в том числе контракты, оформленные в виде ценных рыночных бумаг, обычно предполагают не отдельные или единовременные платежи, а многократные выплаты в различные промежутки времени. В частности, получение кредита может быть распределено во времени. В общем случае взаимоотношения между кредитором и дебитором определяются потоком платежей.

Пусть Т – базовый период, r – процентная ставка для базового периода. В качестве единицы измерения времени будем использовать базовый период T. Пусть t₁, t₂, ¼ t_n – моменты времени, в которые осуществляются выплаты сумм c₁, c₂, ¼c_n – соответственно. Предполагается, что выполнено 0<t₁<t₂<¼<t_n<t, где 0, t – начальный и конечный момент рассмотрения.

Поток платежей удобно представлять графически (см. рис. 3.1).

Рис. 3.1.

Одним из основных элементов финансового анализа являются задачи оценки денежного потока c₁, c₂…,c_n, связанного с реализацией какого - либо проекта или функционированием активов, поступающих в моменты времени t₁, t₂, t_n. В общем случае составляющие потока могут быть связаны между собой.

Для оценки потока платежей удобно использовать две величины:

S(o) – современное значение, приведенный доход или приведенная к начальному моменту денежная сумма, PV (present value);

S(t) – будущее значение или наращенная сумма, FV (future value).

Смысл S(0) (PV) и S(t) (FV) очень прост:

S(0) (PV) – начальная сумма, вложив которую под те же проценты r, можно обеспечить к моменту t возможность выплаты из нее всех рентных платежей;

S(t) (FV) – наращенная сумма определяется путем приведения всех платежей с учетом роста к конечному моменту действия контракта (или к моменту последнего платежа).

Будем считать, что на все время контракта процентная ставка r постоянна. Рассчитаем S(0) – современное значение (PV) или сумму, полученную приведением к начальному моменту, всех платежей с учетом дисконтирования.

Удобно для расчета воспользоваться изображением (см. рис. 3.2).

Рис. 3.2.

Тогда:

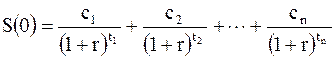(3.1)

Наращенная сумма может быть вычислена двумя способами. Зная S(o), процентную ставку r и длительность сделки t, можно по формуле сложных процентов (2.10) найти будущее значение S(t):

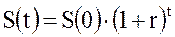(3.2)

С другой стороны, воспользовавшись схемой (см. ниже рис. 3.3), получаем:

Рис. 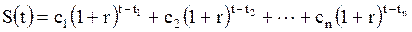3.3.

(3.3)

Можно убедиться, что формулы (3.2) и (3.3) эквивалентны.

Пример 31.

Контракт предусматривает следующий порядок использования кредитной линии: 01.07.2010 г. – 5 млн руб., 1.01.2011 г. – 15 млн руб., 01.01.2013 г. – 18 млн руб. Необходимо определить сумму задолженности на начало 2014г. и современную стоимость этого потока на начало срока при условии, что проценты начисляются по ставке 20 % годовых.

Решение.

Сумма задолженности на начало 2014 г. будет равна:

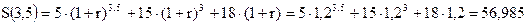млн руб.

Современная стоимость потока на момент выплаты первой суммы равна:

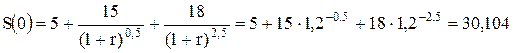млн руб.

Легко проверить, что будущее значение S(3,5) и современное значение S(0) связаны формулой:

.

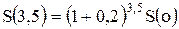Действительно .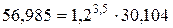

Из представленных выше формул видно: чем больше процентная ставка r, тем больше будущее значение S(t) и тем меньше современное значение S(0). При нулевой ставке r=0 современное и будущее значение совпадают и для данного примера равны S(0)=S(t) =38 млн руб.