Применение формулы непрерывного дисконта при оценке инфляции

Инфляции на капитал действует непрерывно, каждую наносекунду, и её влияние будет описываться дифференциальным уравнением вида:

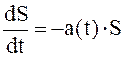, (2.34)

где – скорость изменения (убывания) капитала; S(t) – капитал;

a(t) – непрерывный дисконт (уровень инфляции).

Из (2.34) при инфляции a(t)>0 и капитале S>0 производная от капитала dS/dt < 0 отрицательна и, следовательно, капитал S(t) убывает. После интегрирования дифференциального уравнения (2.34) имеем для зависимости капитала от времени действия инфляции:

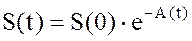(2.35)

где S(0) – начальная сумма в момент 0;

S(t) –конечная сумма в момент t;

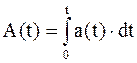- определенный интеграл от инфляции a(t).

Пример 30.

В начале года у господина А имеется 100 тысяч рублей. Какова реальная стоимость этой суммы в конце года, если господин А держит деньги в «чулке»? Под какой процент должны быть вложены деньги, чтобы они не обесценились? Рассмотреть случаи, когда:

1. Инфляция меняется по линейному закону: в начале года она составляет 21 %, а в конце года 9 %.

2. Инфляция меняется по параболическому закону: в начале года она составляет 21 %, а в конце года 9 %. Парабола имеет максимум в начале года при t =0.

3. Инфляция меняется по параболическому закону: в начале года она составляет 21 %, а в конце года 9 %. Парабола имеет минимум в конце года при t =1.

Решение.

Легко видеть (см. рис 2.3), что формулы, описывающие зависимость инфляции (непрерывного дисконта) от времени имеют соответственно вид:

1. a(t) = -12 t+21; 2. a(t) = -12 t²+21; 3. a(t) = 12 (t-1)²+9 (%/год).

Воспользуемся формулой (2.35) для оценки капитала в конце года, для этого сначала нужно вычислить интегралы A(t). Для случаев 1, 2, 3 имеем соответственно:

1. ;

2. ;

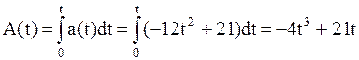3. .

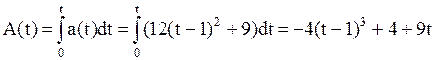Для определения капитала в конце года нужно в формулу (2.35) и полученные интегралы подставить t =1 год. Тогда, получим:

1. А(1)=15 %, 2. А(1)=17 %, 3. А(1)=13 %.

Полученные значения имеют экономический смысл. Это среднегодовая инфляция. Для линейного закона изменения инфляции она равна 15 % (случай 1), для параболических законов изменения инфляции она равна соответственно 17 % (случай 2) и 13 % (случай 3).

Чтобы деньги не обесценились, они должны быть вложены под процент, превышающий среднегодовую инфляцию.

Найдем теперь реальную стоимость суммы в конце года с учетом инфляции. Из (2.34) при t =1 получим соответственно:

1. S(1) = S(0) e ^{- 0,15} = 100* 0,86071=86,071 тыс. руб.;

2. S(1) = S(0) e ^{- 0,17} = 100* 0,84366=84,366 тыс. руб.;

3. S(1) = S(0) e ^{- 0,13} = 100* 0,87809=87,809 тыс. руб.

При малых значениях процентной ставки возможен упрощенный расчет с использованием замечательного предела . Приблизительное значение суммы в конце года равно соответственно 85 тыс. руб., 83 тыс. руб. и 87 тыс. руб. Очевидно, эти значения близки к суммам, посчитанным по точным формулам.

ПОТОКИ ПЛАТЕЖЕЙ