ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ
В финансовом анализе огромную роль играет время. Эта роль велика даже при малой инфляции, а при большой инфляции она является решающей. Все знают на собственном опыте, что 100 тыс. руб. сегодня и через месяц могут оказаться различными деньгами. Например, при запланированной инфляции 20 % приведенная выше сумма в 100 тыс. руб., если держать ее дома, через год превратится в 100(1-0,2)=80 тыс. руб. Второй пример, предположим, что вам должны вернуть долг в 100 тыс. руб. и рассматриваются два варианта возврата денег. В первом варианте предлагают его отдать по частям: 50 тыс. руб. через полгода и остальные 50 тыс. руб. через год. Во втором варианте предполагается возврат всей суммы сразу через год. Очевидно первый вариант для кредитора лучше.
С другой стороны, если у вас имеются накопления в рублях, долларах, евро, иенах, юанях и т. д. или в ценных бумагах, то в каждый момент времени эти накопления имеют разную курсовую стоимость. Последнее особенно ощутимо в условиях кризиса.
В связи с этим в финансовых вычислениях чрезвычайно важно учитывать время. Поэтому, в частности, в экономических расчетах денежные суммы нельзя просто так складывать, без учета зависимости капитала от времени. Ниже будут приведены методы, позволяющие учесть зависимость капитала от времени в финансовых вычислениях.
Ценная бумага удостоверяет определенную финансовую операцию (сделку). Не конкретизируя вид ценной бумаги, изложим основные математические методы, позволяющие оценить выгодность и эффективность данной операции (сделки). В примерах и задачах будут приведены варианты расчетов эффективности для основных видов ценных бумаг.
Основные понятия
Простейшей финансовой операцией является однократное предоставление в долг некоторой суммы. В этой сделке присутствуют два лица – кредитор и дебитор. Эта финансовая операция характеризуется следующими временными параметрами и денежными величинами.
Пусть функция S(t) описывает зависимость капитала S от времени t. Простейшая финансовая сделка сводится к однократному предоставлению в долг некоторой суммы S(t) с условием возврата суммы S(t+T) через время Т.
Для оценки эффективности операции используются два показателя:
- относительное приращение суммы или капитала (процентная ставка, процент, ставка процента, рост, норма прибыли, доходность, интерес, interest rate, return)
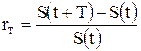 , (2.1)
, (2.1)
отсюда
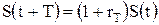 ; (2.2)
; (2.2)
- относительная скидка или относительное уменьшение конечного капитала (учетная ставка, дисконт, discount rate)
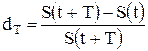 , (2.3)
, (2.3)
отсюда
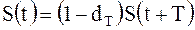 , (2.4)
, (2.4)
где S(t) – капитал в начальный момент t (начальный вклад);
S(t+T) – капитал в конечный момент t+T (конечная сумма).
Таким образом, в любой финансовой операции присутствуют три величины, две из которых заданы, а одна неизвестна. В соответствии с этим возникают различные экономические задачи, которые будут рассмотрены ниже. Наличие двух показателей эффективности процентной ставки r и дисконта d связано с тем, что процесс наращивания и процесс дисконтирования отличаются направлением потока денежных средств.

 | |||
 |

Рис. 2.1
Если время сделки Т постоянно, то Т называют базовым периодом, а rT – часто называют процентной ставкой и dT – дисконтом. Очевидно, процентная ставка и дисконт не являются независимыми показателями эффективности сделки. Они связаны соотношениями:
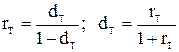 . (2.5)
. (2.5)
Вместо дисконта иногда используют математический дисконт фактор, равный
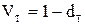 . (2.6)
. (2.6)
Очевидно
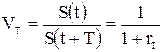 . (2.7)
. (2.7)
Рост и дисконт являются безразмерными величинами и обычно выражают в процентах.
Пример 1.
Ссуда в размере 2 млн руб. дана на 1 год с условием возврата 4 млн руб. В этом случае процентная ставка равна:
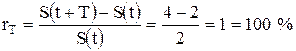 ,
,
дисконт равен 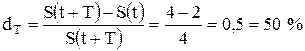 .
.
Пример 2.
Кредит выдан на 5 млн руб. с кредитной ставкой 50 % годовых. Тогда, через год следует вернуть:
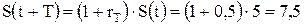 млн руб.
млн руб.
Пример 3.
Кредит выдан с условием возврата через год 5 млн руб. и дисконтом 30 %. Тогда дебитор получит:
 млн руб.
млн руб.
При этом дисконт фактор равен 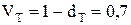 .
.
Задача 1.
Предприниматель обратился в банк с просьбой о предоставлении ссуды в размере 1млн руб. на срок 1 год. Банк выделил ему эту ссуду с годовой учетной ставкой 20 %. Определить сумму, возвращаемую предпринимателем банку через год.
Ответ.
1,25 млн руб.
Для удобства сравнения финансовых операций процентные ставки, дисконт приводят к базовому периоду – обычно году. Отсюда возникает задача: имея процентные ставки и дисконт за базовый период Т, вычислить соответствующие величины за фактический период действия сделки.
Правила начисления процентов оговариваются при заключении сделки и сводятся к схемам простых процентов (simple interest), сложных процентов (compound interest) и смешанных процентов. Суть данных схем заключается в следующем.
Кредитование
Простые ставки процентов. Пусть начальный момент равен нулю, Т – базовый период, t – фактический период действия сделки, называемый конверсионным периодом или периодом начисления, S(o) – начальная сумма, S(t) – конечная сумма, получаемая кредитором в момент t. Если годовой интерес (ставка) равна r, то в конце фактического срока сделки t дебитор должен заплатить кредитору сумму
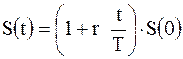 , (2.8)
, (2.8)
где t и Т измеряются в днях. При этом согласно договору, используется либо точная длительность года – 365 или 366 дней (точные проценты), либо приближенная длительность года – 360 дней = 12 месяцев ´30 дней (обычные проценты).
В ряде случаев удобно использовать упрощенную форму записи формулы простых процентов в виде:
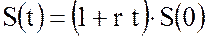 , (2.9)
, (2.9)
где фактический период действия сделки t измеряются в годах. При этом переход от длительности сделки в днях к длительности сделки в годах производится по схемам обычных или точных процентов.
Таким образом, в формуле (2.9), описывающей финансовую операцию, присутствуют четыре параметра. Можно задать любые три параметра, а четвертый параметр считать неизвестным. Определить его можно из уравнения (2.9).
В соответствии с этим возникают различные экономические задачи, которые будут рассмотрены ниже.
Пример 4.
Выдан кредит на сумму 7 млн руб. с 09.02.2013 г. по 21.09. 2013 г. под
16 % годовых. В зависимости от договора сумма погасительного платежа различна. При точном расчете t=16 дней (январь) + 28 дней (февраль) +15 дней (март) = 59 дней согласно (2.8) имеем:
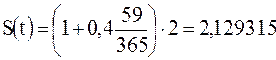 млн руб.
млн руб.
Приближенный расчет по обычным процентам дает согласно (2.8) t=60 дней:
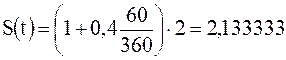 млн руб.
млн руб.
Сумма платежа по обычным процентам всегда больше чем по точным процентам.
Пример 5.
Определить простую ставку процентов, при которой первоначальный капитал в размере 60 млн руб. достигнет 63 млн руб. через квартал.
Из формулы простых процентов (2.9) для ставки r имеем:
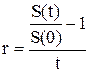
Подставляя соответствующие числовые значения, получим:
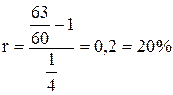
Пример 6.
Определить период начисления, за который первоначальный капитал в размере 38 млн руб. вырастет до 40 млн руб., если используется простая ставка процентов 12 % годовых.
Из формулы простых процентов (2.9) для времени t имеем:
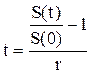
Тогда, подставляя соответствующие числовые значения, получим:
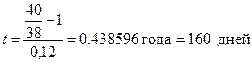
Пример 7.
Кредит выдается под простую ставку 16 % годовых на 250 дней. Рассчитать сумму, получаемую заемщиком, и сумму процентных денег, если требуется возвратить 50 млн руб.
Из формулы простых процентов (2.9) имеем:
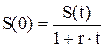
Следовательно, сумма, получаемая заемщиком равна:
S(0)=50/(1+0,16·250/360)= 45 млн руб.,
Сумма процентных денег равна 5 млн руб.
Задача 2.
Ссуда в размере 50 тыс. руб. выдана на полгода по простой ставке процентов 28 % годовых. Определить наращенную сумму.
Ответ.
57 тыс. руб.
Задача 3.
Кредит в размере 10 млн руб. выдан 2 марта до 11 декабря под 30 % годовых, год високосный. Определить размер наращенной суммы для различных вариантов расчета процентов: точное число дней ссуды и точная длительность года 366 дней; точное число дней ссуды и приближенная длительность года 360 дней; приближенные число дней ссуды и длительность года.
Ответ.
12327868 руб.;
12366666 руб.;
12333333 руб.
Задача 4.
Определить период начисления, за который первоначальный капитал в размере 25 млн руб. вырастет до 40 млн руб., если используется простая ставка процентов 28 % годовых.
Ответ.
t=2,14 года.
Задача 5.
Определить простую ставку процентов, при которой первоначальный капитал в размере 24 млн руб. достигнет 30 млн руб. через год.
Ответ.
r=25 %.
Задача 6.
Кредит выдается под простую ставку 26 % годовых на 250 дней. Рассчитать сумму, получаемую заемщиком, и сумму процентных денег, если требуется возвратить 40 млн руб.
Ответ.
33,955857 млн руб.;
6,044143 млн руб.
Задача 7.
В течение первого месяца цена товара увеличилась на 25 %, а в течение следующего месяца цена товара возвратилась к первоначальному уровню. На сколько процентов уменьшилась новая цена товара?
Ответ.
На 20 %.
Задача 8. Переменная ставка простых процентов.
За время хранения вклада меняются величины процентных ставок. Пусть в периоды времени n1, n2, … nm процентные ставки составляют r1, r2,… rm. Найти наращенную сумму S(t), если начальный вклад равен S(0).
Ответ.
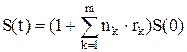
При расчетах по среднесрочным и долгосрочным кредитам используется схема сложных процентов.
Сложные проценты. Пусть длительность сделки t кратна базовому периоду Т, т. е. t целое число. При базовом периоде Т = 1 год, длительность сделки целое число лет t. Тогда наращенная сумма равна:
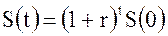 , (2.10)
, (2.10)
где
S(0) – начальная сумма,
r – процентная ставка за год (интерес).
Очевидно, что зависимость суммы S(t) от времени t при расчете по схеме простых процентов (2.9) линейная, при расчете по схеме сложных процентов нелинейная (является показательной функцией от t), и, как будет показано ниже, в ряде случаев эта зависимость хорошо апроксимируется экспонентой.
Формула (2.10) может использоваться для расчета по сложным процентам при любой длительности сделки t так, как показательная функция определена при любых значениях t.
Пример 8.
Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании простой и сложной ставки процентов в размере 28 % годовых. Рассмотреть случаи, когда сложные проценты начисляются ежегодно, по полугодиям и поквартально. Для простых процентных ставок имеем:
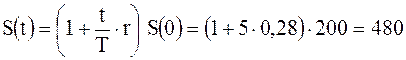 тыс. руб.
тыс. руб.
Для сложных годовых процентов:
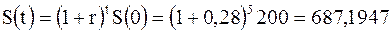 тыс. руб.
тыс. руб.
Для сложных полугодовых начисленных процентов:
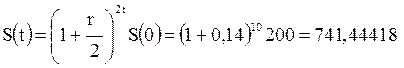 тыс. руб.
тыс. руб.
Для поквартального начисления сложных процентов:
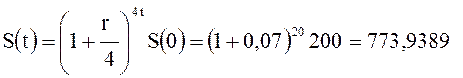 тыс. руб.
тыс. руб.
Обобщая пример 5, рассмотрим задачу вычисления процентной суммы S(t) через t лет в случае, когда проценты начисляются m раз в год. Сумма S(o) выдана под r процентов годовых с начислением сложных процентов m раз в год. Воспользовавшись формулой (2.10), для этого случая очевидно имеем:
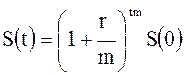 . (2.11)
. (2.11)
Представляет интерес рассмотрения предельного случая при m®¥, тогда сложные проценты начисляются непрерывно. Используя замечательный предел
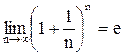 ,
,
где 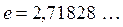 – основание натуральных логарифмов (число «е»), получим:
– основание натуральных логарифмов (число «е»), получим:
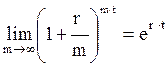 .
.
Таким образом, если сложные проценты начисляются непрерывно, наращенная сумма экспоненциально зависит от времени и равна:
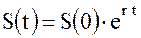 (2.12)
(2.12)
Наращение суммы при непрерывном начислении процентов идет более быстрым темпом, чем при начислении сложных дискретных процентов.
Для примера 5 в случае непрерывного исчисления имеем:
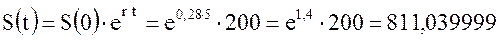 тыс. руб.
тыс. руб.
Смешанные или комбинированные проценты. Пусть Т – базовый период, а t – фактическая длительность сделки. Всякое число можно представить в виде суммы целой и дробной части:
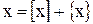 ,
,
где
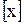 – обозначает целую часть числа;
– обозначает целую часть числа;
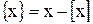 – дробную часть числа.
– дробную часть числа.
Разобьем длительность сделки в годах 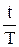 на целую и дробную часть
на целую и дробную часть 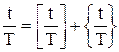 . Обозначим для простоты
. Обозначим для простоты 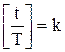 и
и 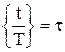 , тогда
, тогда 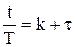 .
.
Используя приведенные обозначения, для наращенной суммы, вычисленной по схеме комбинированных процентов, имеем:
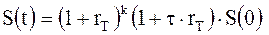 , (2.13)
, (2.13)
где
k – целая часть 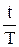 или целое число лет в длительности сделки;
или целое число лет в длительности сделки;
t – дробная часть длительности сделки 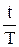 .
.
Пример 9.
Первоначальная сумма долга равна 50 млн руб. Определить наращенную сумму долга через 2,5 года, используя способ начисления смешанных процентов по ставке 25 % годовых.
Для смешанных или комбинированных процентов имеем согласно формуле (2.12):
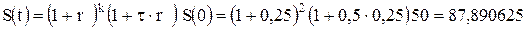 млн руб.
млн руб.
Пример 10.
31 марта 2010 г. была получена в долг сумма 40 тыс. руб. под 32 % годовых. Долг был возвращен 11 июня 2013 г. Какая сумма была возвращена?
При использовании в расчетах комбинированных процентов согласно (2.12) получается сумма:
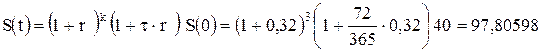 тыс. руб.
тыс. руб.
При расчете кредитования могут возникать различные задачи. В формуле для сложных процентов (2.10) и непрерывных процентов (2,12), имеется четыре параметра. Можно задать любые три из них, а четвертый параметр определить из уравнения (2.10) или (2,12). В соответствии с этим возникают различные экономические задачи. Например, следующие.
Пример 11.
За какой срок первоначальный капитал 50 млн руб. увеличится до 200 млн руб., если:
а) на него начисляются сложные проценты по ставке 28 % годовых;
б) проценты начисляются ежеквартально;
в) проценты начисляются непрерывно?
Решение.
Согласно (2.9) для случая «а» начальная и конечная суммы связаны соотношением 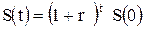 .
.
Отсюда, находим время t:

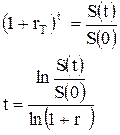
Подставляя численные значения, имеем:
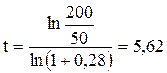 года.
года.
Аналогично, согласно (2.11) для случая «б», когда проценты начисляются раз m в год, имеем уравнение для определения длительности сделки 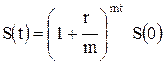 .
.
Решая уравнение, имеем:
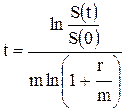 . (2.14)
. (2.14)
В нашем случае при r=0,28, m=4, S(0)=50 млн руб., S(t)=200 млн руб. для времени накопления капитала получим:
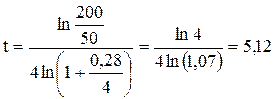 года.
года.
Для определения периода начисления в случае «в», когда проценты начисляются непрерывно, воспользуемся формулой (2.12). Решая уравнение (2.12) относительно t получим:
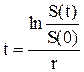 (2.15)
(2.15)
Формула для расчета времени (2.15) может быть получена также из (2.14) предельным переходом при m®¥. При этом нужно воспользоваться замечательным пределом 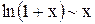 при малых
при малых
значениях x.
Подставляя численные значения в (2.15), имеем:
t=ln(200/50)/0,28=4,95 года
Таким образом, чем чаще начисляются проценты, тем быстрее происходит накопление капитала.
Пример 12.
Если цены растут на 2 % ежемесячно, то часто за годовой уровень инфляции принимают 24 %, и банки привлекают клиентов, обещая 25 %. Каков уровень инфляции? Какую прибыль имеют клиенты банка?
Решение.
Пусть стоимость S(0) товара в начале года. Тогда, при месячном уровне инфляции r стоимость товара в конце года будет равна в соответствии с формулой сложных процентов (2.10) величине:
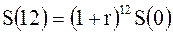
Приращение стоимости товара за год составит:
S(12)-S(0)=(1+r)12S(0)-S(0)=((1+r)12 - 1) S(0)
Следовательно, годовая инфляция, равная относительному повышению стоимости товара, будет иметь вид:
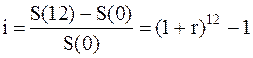 (2.16)
(2.16)
Таким образом, при месячном уровне инфляции r=2 % годовая инфляция будет составлять:
i = (1+0,02)12 - 1=26,82 %
В этом случае клиенты банка терпят убытки в размере 1,82 %.
Учитывая что, инфляция действует непрерывно каждую наносекунду, расчет годовой инфляция может быть произведен по формулам для непрерывных процентов (2.12). Действительно, в этом случае стоимость товара в конце года будет равна:
S(12)=S(0) e12 r
Приращение стоимости:
S(12)-S(0)=(e12 r-1) S(0)
Годовая инфляция (относительное повышению стоимости товара за год), будет равна:
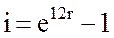 (2.17)
(2.17)
или в нашем случае:
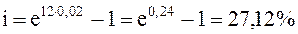
Очевидно, годовая инфляция 27,12 %, вычисленная по формулам непрерывных процентов, чуть больше годовой инфляции 26,82 %, рассчитанной по формулам сложных процентов.
Пример 13.
Банк предлагает потребительский кредит под 3 % в месяц. Какова годовая процентная ставка кредита?
Решение.
На первый взгляд кажется, что годовая процентная ставка кредита равна 3 %*12=36 %. Однако, правильное значение ставки получается с учетом формул сложных процентов. Используя рассуждения, аналогичные приведенным в примере 12, получим правильное значение процентной ставки в виде (см. формулу 2.16):
rгод=(1+r)12-1 = (1+0,03)12-1=42,58 %
Таким образом, истинное значение годовой процентной ставки потребительского кредита 42,58 % превышает предполагаемое значение 36 % на 6,8 %.
Удвоение капитала. Правило 72. В банк под r процентов годовых вложен капитал. Для клиента банка процентная ставка r является достаточно абстрактной величиной. Ему хотелось бы знать, за какой срок капитал удвоится при этой ставке?
Предположим сначала, что проценты начисляются непрерывно. Тогда, воспользовавшись формулой для непрерывных процентов (2.12), получим для времени удвоения капитала из (2.15) формулу:
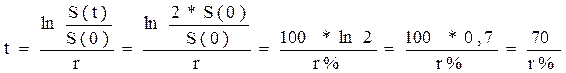 ,
,
где r%=100*r ставка в процентах.
Таким образом, в случае непрерывного начисления процентов получается точное «правило 70», т. е. время за которое капитал удвоится равно70/r %, где r выражено в процентах. Например, при r% =10 % капитал увеличится в два раза за 7 лет.
В банке проценты начисляются дискретно раз в год, раз в полгода, раз в квартал. При этом время удвоения капитала немного возрастает и в банковском деле используется полуэмпирическая формула «правило 72» в виде:
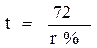 (2.18)
(2.18)
Правило 72: Если процентная ставка есть r%, то удвоение капитала произойдет через 72/ r %.
В таблице 1.1 приведена зависимость времени удвоения капитала от процентной ставки:
Таблица 1.1
| r % | t годы |
| 5 % | 14,4 |
| 10 % | 7,2 |
| 20 % | 3,6 |
Дадим дополнительное обоснование цифре 72 в формуле (2.18) («правило 72»). В дискретном случае, при начислении r процентов годовых m в год в течение t лет, для накопленного капитала имеем формулу (2.11).
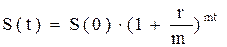 .
.
Отсюда, аналогично (2.14) для срока удвоения капитала получим:
где 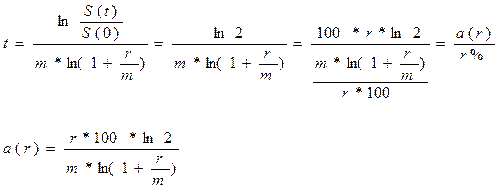
Видно, что a(r) в дискретном случае не является постоянной величиной. Она зависит от процентной ставки r и количества периодов начисления m. Однако, при малых значениях ставки r, в силу замечательного предела, ln(1+r/m) примерно равен r/m и, следовательно, a(r) приблизительно равно 70 и мало меняется. Действительно, произведем вычисления a(r) для некоторых реально встречающихся процентных ставок r и количеств периодов начисления m.
Таблица 1.2
| r % | m=4 | m=2 | m=1 |
| a (r) | a (r) | a (r) | |
| 8 % | 70,69 | 72,05 | |
| 10 % | 70,17 | 71,03 | 72,72 |
| 12 % | 70,34 | 71,37 | 73,39 |
Из таблицы 1.2 видно, что в большинстве реальных случаев начисления процентов a(r) действительно близко к 72 и, следовательно, «правило 72» верно.
Сравнение кредитования по схеме простых и сложных процентов
Оценим выгодность для кредитора схем кредитования по простым и сложным процентам. В качестве показателя эффективности кредитования используем относительное приращение капитала:
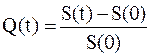 , (2.19)
, (2.19)
где t - период начисления, S(0) - выданная сумма, S(t) - полученная сумма.
Тогда, из (2.9) показатель эффективности длякредитования по схеме простых процентов будет равен линейной по длительности t сделки функции:
Q(t) = r t (2.20)
Показатель эффективности длякредитования по схеме сложных процентов из (2.10) будет равен показательной по t функцией:
Q(t)= (1+r) t - 1 (2.21)
При длительности сделки равной нулю (t=0), её эффективность Q(t) очевидно равна нулю. Если длительность сделки равна году (t=1), то показатели эффективности кредитования по схемам простых и сложных процентов одинаковы и равны r. Чтобы разобраться с общим случаем, построим график зависимости показателей эффективности Q(t) от длительности сделки t.
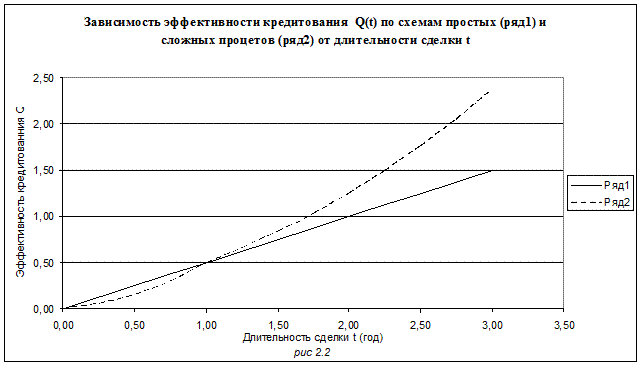
Из графика (см. рис. 2.2) видно, что при длительности сделки меньше года для кредитора более выгодна схема кредитования по простым процентам, при длительности сделки больше года для кредитора более выгодна схема кредитования по сложным процентам.
Пример 14.
Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через полгода и три года при использовании простой и сложной ставки процентов в размере 50 % годовых.
Решение.
Из (2.8) наращенная по простым процентам сумма через полгода и три года будет равна соответственно:
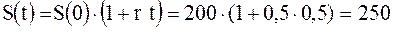 тыс. руб.,
тыс. руб.,
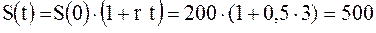 тыс. руб.
тыс. руб.
Из (2.9) наращенная по сложным процентам сумма через полгода и три года будет равна соответственно:
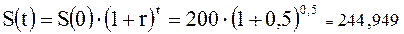 тыс. руб.,
тыс. руб.,
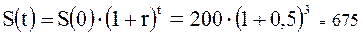 тыс. руб.
тыс. руб.
Таким образом, при сроке кредитования полгода для кредитора более выгоден расчет по простым процентам. Возвращаемая сумма, рассчитанная по схеме простых процентов равна 250 тыс. руб., по схеме сложных процентов 244,949 тыс. руб. При сроке кредитования три года более выгоден расчет по сложным процентам. Возвращаемая сумма, рассчитанная по схеме простых процентов равна 500 тыс. руб., по схеме сложных процентов 675 тыс. руб.
Задача 9. Переменная ставка сложных процентов.
За время хранения вклада меняются величины процентных ставок. Пусть в периоды времени n1 , n2 … nm процентные ставки составляют r1 , r2 , rm. Найти наращенную сумму S(t), если начальный вклад равен S(0).
Ответ.
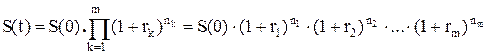
Дисконтирование
Вычисление дисконта или дисконт-фактора за произвольный период времени t также производится по ставке r или дисконту d за базовый период Т (обычно год) по различным схемам: простых, сложных или комбинированных процентных ставок.
Простые ставки. Банковский дисконт (bank rate). Данная схема применяется в банковских расчетах при покупке или учете банковских краткосрочных обязательств (векселей).
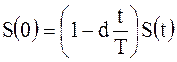 , (2.22)
, (2.22)
где
d – базовый дисконт, базовая учетная ставка;
T – базовый период (год);
t – расчетное время действия сделки, конверсионный период или период начисления;
S (t) – стоимость векселя в будущем в момент t;
S (0) – стоимость покупки векселя в настоящий момент o.
При этом согласно договору, используется либо точная длительность года – 365 или 366 дней (точные проценты), либо приближенная длительность года – 360 дней = 12 месяцев ´30 дней (обычные проценты).
Пример 15.
Вексель выдан на сумму 2 млн руб. и содержит обязательство выплатить владельцу эту сумму 15.03.2010 г. Владелец предъявил банку вексель досрочно 01.02.2010 г., банк согласился выплатить сумму (учесть вексель), но с дисконтом 40 % годовых. Полученная сумма будет равна:
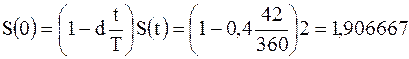 млн руб.
млн руб.
Формула простых процентов (2.22) может быть использована лишь при
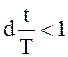 .
.
В частности, лишена смысла операция учета векселя за год с годичным дисконтом d более 100 %.
Математический дисконт-фактор, равный 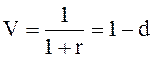 более универсален.
более универсален.
Действительно, при расчете дисконтирования по сложным процентам получаются из (2.6) и (2.10):
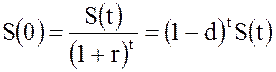 , (2.23)
, (2.23)
где
t– длительность сделки;
Пример 16.
Определить современную (текущую, настоящую, приведенную) величину суммы 100 млн руб., выплачиваемую через три года при использовании ставки сложных процентов 24 % годовых.
Воспользовавшись формулой (2.23) имеем:
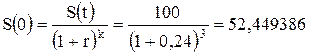 млн руб.
млн руб.
Если, согласно контракту, применяется схема дисконтирования несколько раз в течение года, то оговаривается годовой дисконт (годовая учетная ставка) и число расчетов m в течение года. Тогда приведенная сумма равна:
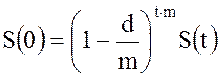 . (2.24)
. (2.24)
Пример 17.
Вексель на 3 млн руб. с годовой учетной ставкой 10 % с дисконтированием 4 раза в год выдан на 2 года.
Тогда исходная сумма, которая должна быть выдана в долг под вексель согласно (2.24) равна:
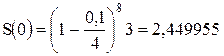 млн руб.
млн руб.
Дата добавления: 2016-03-15; просмотров: 7295;
