Ставка процента, учитывающая инфляцию. Формула Фишера.
Пусть rn – ставка процента, учитывающая инфляцию (номинальная ставка процента), r - реальная ставка банковского процента (реальная процентная ставка), i ставка темпа инфляции.
Пусть S(0) - капитал в начале года. Тогда, капитал в конце года с одной стороны должен быть равен:
S(1) = (1+rn) S(0).
С другой стороны он равен:
S(1) = (1+i) (1+r) S(0).
Приравнивая капиталы в конце года, вычисленные по разным формулам, получим формула Фишера, связывающую номинальную rn и реальная r ставка процента с темпом инфляции i:
rn = r + i + i r (2.25)
Величина i r– называетсяинфляционной премией.
Пример 18.
Банк начисляет проценты по номинальной ставке 16 %. Уровень инфляции составляет 12 %. Определить реальную ставку банковского процента с учетом инфляционной премии.
Из формулы Фишера вычисляем реальную процентную ставку r через номинальную ставку процента rn и темп инфляции i:
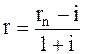 .
.
В нашем случае получим:
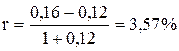
Таким образом, при большой инфляции реальная ставка банковского процента, равная 3,57 %, меньше разности между номинальной ставкой и инфляцией 16 % - 12% = 4 %.
Пример 19.
Первоначальный капитал в размере 200 тыс. руб. выдается на три года, проценты начисляются в конце каждого квартала по номинальной ставке 8 %. Уровень инфляции составляет 12 %.
Определить наращенную сумму с учетом и без учета инфляционной премии.
Наращенная сумма без учета инфляции из (2.11) равна:
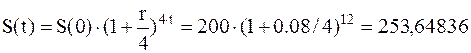 тыс. руб.
тыс. руб.
Наращенная сумма с учетом инфляции может быть вычислена по формуле сложных процентов (2.10):
 тыс. руб.
тыс. руб.
В связи с тем, что уровень инфляции больше чем номинальная процентная ставка, наращенная сумма с учетом инфляции меньше первоначального капитала.
Пример 20.
Имеется вексель следующей формы:
«20000 руб. Санкт-Петербург. 1 сентября 2010 г. Обязуюсь уплатить через 60 дней после данной даты по распоряжению гражданина А 20000 руб. с процентной ставкой 11 % годовых.
/подпись/ гражданин В».
За сколько банк купит вексель 1 октября 2010 г., если банковская процентная ставка 9,5 %?
Решение.
Сумма, которую должен получить гражданин А через 60 дней вычисляется по схеме простых процентов и равна 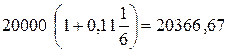 руб.
руб.
Отсюда получается уравнение: 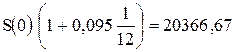 руб.,
руб.,
где S(0) – сумма, которую уплатит банк за вексель.
Окончательно S(0)=20206,70 руб.
Задача 10.
В течение первого месяца цена товара увеличилась на 30 %, а в течение следующего месяца новая цена товара уменьшилась на 10 %. На сколько процентов изменилась цена товара за 2 месяца?
Ответ.
на 17 %.
Эффективная ставка
Формула сложных процентов (2.10) включает четыре неизвестных S(0), S(t), r, t. Зная три неизвестных из уравнения (2.10) можно определить четвертое неизвестное. Сама формула сложных процентов (2.10) определяет будущий капитал S(t) через настоящий капитал S(0), процентную ставку r и время t.
В примере 11 находится время t накопления капитала при известных значениях настоящего S(0) и будущего капитала S(t) и процентной ставки r. В предыдущем разделе, посвященном дисконтированию, в формуле (2.23) современное значение S(0) капитала определяется по его будущему значению S(t), процентной ставке r и времени t. Из формулы сложных процентов (2.10) не определялась только процентная ставка r через настоящий S(0) и будущий S(t) капитал и время t. Решение этой задачи связано с очень важным экономическим понятием эффективной ставки.
Для сравнения различных вариантов сделок удобно использовать эффективную ставку 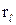 .
.
Эффективной называют годичную ставку 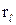 сложных процентов, обеспечивающую заданное отношение полученной суммы S(t) к выданной сумме S(0), независимо от того, какая схема оплат используется в данной конкретной сделке.
сложных процентов, обеспечивающую заданное отношение полученной суммы S(t) к выданной сумме S(0), независимо от того, какая схема оплат используется в данной конкретной сделке.
Из (2.10) имеем уравнение для определения 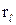 :
:
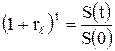 ,
,
где t – длительность сделки в годах.
Тогда:
 . (2.26)
. (2.26)
Очевидно, что эффективная ставка не зависит от объемов конкретных сумм S(0) и S(t), а определяется только отношениями этих сумм.
Пример 21.
Найти эффективную ставку сделки, в результате которой первоначальный капитал утроился за 5 лет.
Согласно (2.26) имеем 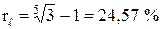 .
.
Пример 22. Удвоение ВВП.
Найти ежегодный темп роста ВВП, при котором он удвоится за 10 лет, за 7 лет, за 3 года.
Решение:
Воспользовавшись формулой эффективной ставки (2.26):
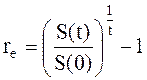 ,
,
получим ежегодный темп роста ВВП, соответственно, для 10 лет, 7 лет и
3-х лет
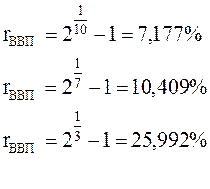
Пример 23.
В долг дана сумма 2 млн руб. с условием возврата через 2,5 года 3 млн руб. Тогда эффективная ставка в данный сделке равна:
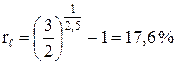 .
.
Пример 24.
Выдан кредит в 2 млн руб. на 3 месяца под 100 % годовых. Найти эффективную ставку.
Учитывая, что кредит краткосрочный, сумма, выплачиваемая через 3 месяца, будет равна:
 млн руб.
млн руб.
тогда эффективная ставка будет равна:
 , где S(0)=2 млн руб., S(t)=2,5 млн руб.,
, где S(0)=2 млн руб., S(t)=2,5 млн руб., 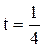 года.
года.
 .
.
Пример 25.
Вексель выдан на сумму 50 млн руб. и содержит обязательство выплатить владельцу эту сумму через 4 месяца. Владелец предъявил банку вексель досрочно. Банк согласился учесть вексель, но с дисконтом 24 % годовых. Найти эффективную ставку.
Решение:
Полученная сумма будет равна:
 млн руб.
млн руб.
Тогда эффективная ставка будет равна:
 , где S(0)=46 млн руб., S(t)=50 млн руб.,
, где S(0)=46 млн руб., S(t)=50 млн руб., 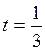 года.
года.
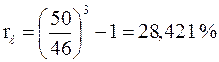 .
.
Пример 26.
Вексель 3 млн руб. выдан на 2 года с годовой учетной ставкой 10 % с дисконтированием 2 раза в год. Найти эффективную ставку. По формуле (2.24) найдем исходную сумму, выплаченную по векселю:
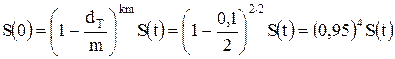 .
.
Тогда 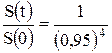 . Следовательно, для эффективной ставки имеем:
. Следовательно, для эффективной ставки имеем:
 .
.
Пример 27.
Остров Манхеттен был продан в 1624 г. за $24. В 1976 г. его стоимость была $40×109. Какова эффективная ставка сделки?

Решение:
В данной задаче интуиция обманывает человека: кажется, что эффективная процентная ставка будет очень большой. Однако расчет по формуле (2.26) даёт следующее значение:
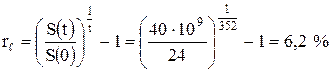 .
.
Решающим фактором, приводящим к столь скромному значению эффективной процентной ставки, является время. Длительность сделки велика ‑ 352 года.
В ряде случаев для сравнения различных вариантов сделок вместо эффективной ставки 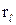 используется процентная спот-ставка rs. Она определяется аналогично эффективной ставки, только вместо сложных процентов используются непрерывные проценты.
используется процентная спот-ставка rs. Она определяется аналогично эффективной ставки, только вместо сложных процентов используются непрерывные проценты.
Процентной спот-ставкой называют годичную ставку rs непрерывных процентов, обеспечивающую заданное отношение полученной суммы S(t) к выданной сумме S(0), независимо от того, какая схема оплат используется в данной конкретной сделке.
Из (2.12) имеем уравнение для определения rs:
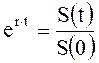 ,
,
где t – длительность сделки в годах.
Тогда, после логарифмирования имеем:
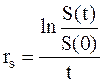 . (2.27)
. (2.27)
Очевидно, что спот-ставка не зависит от объемов конкретных сумм S(0) и S(t), а определяется только отношениями этих сумм.
Спот-ставка всегда меньше эффективной ставки сделки.
Задача 11.
Для примеров 21-27 найти спот-ставки rs.
Ответы:
Пример 21. rs =  = 21,972%;
= 21,972%;
Пример 22. rs = 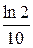 =6,931%, rs =
=6,931%, rs =  =9,902%, rs =
=9,902%, rs = 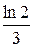 =23,105%;
=23,105%;
Пример 23. rs = 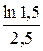 =16,219%;
=16,219%;
Пример 24. rs = 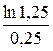 =89,257%;
=89,257%;
Пример 25. rs =3 ln 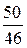 =25,014%;
=25,014%;
Пример 26. rs =-2 ln 0,95=10,259%;
Пример 27. rs =6,032%;
Дата добавления: 2016-03-15; просмотров: 11938;
