Значения инвестиционных платежей и доходов предприятия по отдельным временным интервалам, тыс. руб.

Методически расчет показателя внутренней нормы доходности осуществляется по следующей формуле:

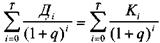(4.1)

или

(4.2)

где Д_i — доход предприятия в i-ом временном интервале

Д_i = J_i • (B_i - C_i) (4.3)

J_i — величина инфляционного коэффициента (см. формулу 3.18) в i-ом временном интервале;

B_i— выручка предприятия в i-ом временном интервале;

С_i — себестоимость продукции (без амортизационных отчислений) в i-ом временном интервале;

К_i — инвестиционные вложения в i-ом временном интервале, которые принимаются по проекту с учетом инфляции национальной валюты

K_i = Ф_Вi-R_i, (4.4)

где Ф_вi — коэффициент инфляции национальной валюты за период от начала инвестирования до 1-го временного интервала

Ф_вi = (1+И₁)(1+И₂)(1+И₃)...(1+И_п), (4.5)

где И₁, И₂, И₃ ... И_п — темпы инфляции национальной валюты в соответствующем временном интервале (в долях от единицы);

R_i — инвестиционные платежи по проекту в i-ом временном интервале (без учета инфляции);

q — показатель внутренней нормы доходности за временной интервал в долях от единицы;

i — текущий временной интервал, принимающий значения от 0 до Т;

Т — длительность жизненного цикла проекта, исчисляемая в принятых временных интервалах.

Произведем расчет (а точнее проверку ранее полученного и приведенного) показателя внутренней нормы доходности по формуле (3.1).

Вначале определим суммарную величину дохода предприятия за весь жизненный цикл проекта (данные для расчета приведены в табл. 4.1).

Теперь подсчитаем суммарные инвестиционные вложения.

Таким образом, условие формулы (4.1) или (4.2) точно выдерживается. Суммарная величина дохода предприятия за весь жизненный цикл проекта, исчисленная с учетом фактора времени и приведенная к началу инвестирования, с высокой точностью соответствует суммарным инвестиционным вложениям, так как 4701,5=4701,5, т.е. показатель внутренней нормы доходности действительно соответствует — q = 0,0698.

Как теперь найти величину искомого показателя, если рассчитать его напрямую по формулам (4.1 или 4.2) при достаточно большом количестве временных интервалов (порядка свыше 4) практически невозможно. В последнее время для расчета внутренней нормы доходности пользуются компьютерными программами, которые в считанные доли минуты определяют искомую величину показателя с достаточной для практики точностью. Разумеется, не всегда под рукой имеется компьютер, а к нему не у всех есть соответствующая программа. Но опытный расчетчик может вручную с помощью обычного калькулятора произвести необходимые вычисления и определить показатель внутренней нормы доходности, затратив на эту процедуру час или несколько больше времени. Все зависит от того, как много временных интервалов используется в расчетах и какова необходимая точность решения поставленной задачи; сама методика проведения расчетных операций не очень обременительна и предполагает постепенное приближение получаемого результата к его окончательному виду в итерационном процессе, при котором с каждым последующим шагом все расчетные операции повторяются, производится коррекция величины показателя и это делается до тех пор, пока искомый результат не будет получен.

Разберем на конкретном примере метод ручного счета внутренней нормы доходности. Для простоты описания воспользуемся проектом, условия которого представлены в табл. 4.1.

Представим всю совокупность расчетных приемов в виде системы последовательных шагов.

1-ый шаг.Определим простую сумму инвестиционных вложений и

∑K_i = (1235 + 1874 + 1963) = 5074 тыс. руб.

Затем найдем сумму доходов предприятия за весь жизненный цикл проекта:

∑Д_i = 0 + 0 + 0 + 502 + 520 +...+ 600 + 600 = 9252 тыс. руб.

Простое сравнение полученных величин свидетельствует о том, что доходная составляющая больше инвестиционной (9252 > 5074). Наличие именно такого неравенства однозначно определяет внутреннюю норму доходности как величину больше нуля. Если бы две сравниваемые величины точно совпадали, то искомый показатель был бы равен нулю. В случае, когда инвестиционная сумма больше доходной составляющей, искомый показатель внутренней нормы доходности будет отрицательной величиной, и, инвестор, скорее всего откажется от такого проекта. Он примет к рассмотрению исследуемый проект только тогда, когда доходы предприятия будут больше инвестиционных вложений. Именно такой случай рассматривается в нашем примере. Поэтому можно перейти к дальнейшему анализу и определению величины внутренней нормы доходности.

2-ой шаг.Установим какую-то величину искомого показателя на определенном уровне, предположим q = 0,1, и произведем расчеты инвестиционных вложений и доходной составляющей проекта с применением принятой нормы доходности по формуле (4.2).

В результате получится отрицательная величина, так как сумма инвестиционных вложений окажется больше доходной составляющей проекта (в чем можно убедиться, произведя соответствующие расчеты). Такой результат свидетельствует о том, что установленная эмпирическим путем величина внутренней нормы доходности должна быть в данном проекте меньше 0,1 и, следовательно, дальнейший поиск связан с некоторым уменьшением величины этого показателя. Обычно, если делать расчет чисто механически, то можно принять для дальнейших расчетов среднее значение показателя между двумя соседними расчетами, т.е., в нашем примере это будет — q = 0,05, так как этот результат и есть средняя между 0 и 0,1.

Приняв новое значение внутренней нормы доходности делают следующий шаг.

3-ий шаг.Все расчеты точно повторяются, но уже с нормой доходности — q = 0,05. При этом разность между доходной и инвестиционной частями проекта может быть либо больше, либо меньше нуля. Если указанная разность меньше нуля, то cледует уменьшить внутреннюю норму доходности (например, до величины — q = 0,025) и все расчеты повторить. Когда разность двух составляющих проекта положительна, т.е., больше нуля (именно так случится в нашем примере, если все расчеты произвести по аналогии с ранее выполняемыми вычислениями), то значение принимаемой нормы доходности надо будет вновь увеличить, доведя ее до величины — q = 0,075. Это значение будет достаточно близким к истинной величине искомой нормы доходности, которое было получено на уровне — q = 0,0698 с помощью компьютерной технологии.

Такие расчеты можно продолжать многократно до получения искомого результата такой степени точности, которая нужна инвестору. В конечном счете, потребность в информации о величине внутренней нормы доходности проекта возникает не так часто, чтобы, снижая трудоемкость операционной работы, отказываться от необходимой точности расчетов.

Показатель внутренней нормы доходности применяется на многих предприятиях и многими инвесторами, но особенно важное значение этот показатель имеет для крупных производств, для масштабных проектов, при реализации которых оценивается их стратегичность и растянутость жизненного цикла, в течение которого проект будет приносить высокий доход.