Приведенный эффект и область его использования
В условиях рынка применение критерия минимума приведенных затрат оказалось достаточно ограниченным и далеко не всегда позволяло отобрать лучший вариант проектного решения. Так возникла потребность модификации минимума приведенных затрат и перехода к более универсальному критерию.
Для решения поставленной задачи посмотрим, к чему приведет нарушение условия 1, если при этом применять показатель минимума приведенных затрат для отбора лучших вариантов. Очевидно, что эти затраты будут больше у того варианта, где больше производственная программа. И если вся выпущенная продукция будет реализована, то такой вариант обеспечит предприятию гораздо лучший результат, чем тот вариант, у которого выпуск продукции будет меньше. Но приведенные затраты у отобранного лучшего варианта окажутся больше, следовательно, в данном случае применять показатель минимума приведенных затрат просто невозможно во избежание искажения результата отбора вариантов.
Аналогичная погрешность будет иметь место при различных уровнях качества выпускаемой продукции, поскольку с улучшением качества затраты на производство продукции возрастают, и, следовательно, приведенные затраты окажутся меньше у варианта с худшим качеством производимой продукции. Проигрыш в этом случае, если останется в действии критерий приведенных затрат, налицо. Поэтому оценка сравнительной эффективности вариантов вложений, если условия 1 и 2 будут нарушены, должна строиться по критерию не минимума затрат, а максимума результата. И это легко проследить с помощью рис. 3.5.
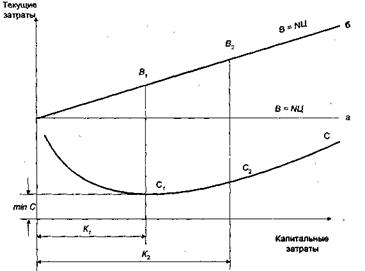
Рис. 3.5. Влияние капитальных затрат на величину результата (прибыли) производства
Когда результат производства в виде выручки предприятия остается постоянным (прямая линия — а) по сравниваемым вариантам в силу того, что у них будут одинаковыми и объем производства, и качество продукции, то становится ясным, почему критерий минимума приведенных затрат обеспечивает правильный отбор лучшего варианта вложений. Он — этот критерий — при постоянной выручке максимизирует результат производства в виде прибыли предприятия посредством минимизации затрат. Но так как постоянная величина на конечный результат сравнения вариантов влияния не оказывает, ее можно отбросить (тем более что эта величина очень часто остается неизвестной и тратить силы и время на ее обоснование нет необходимости). Так как критерий из максимума результата переходит в минимум затрат, то он прекрасно выполняет функцию отбора лучших вариантов вложений для частного случая. Однако распространенность этого частного случая очень велика, и поэтому данный критерий нашел довольно широкое применение не только в плановой экономике (где ему в силу специфики хозяйственного механизма был обеспечен оперативный простор), но и в рыночной экономике при выдерживании указанных условий.
Что же произойдет, если указанные условия будут нарушены и объемы производства по сравниваемым вариантам будут отличаться, либо будут отличаться уровни качества производимой продукции, либо и то, и другое?
В этом случае затраты по вариантам будут существенно возрастать, но также очевидно будут возрастать и результаты производства в виде выручки предприятия (см. линию «б» на рис. 3.5). Тогда, очевидно, критерий должен быть заменен. С минимума затрат надо перейти на максимум результата. Запишем условие выгодности более капиталоемкого варианта из двух альтернативных вариантов:
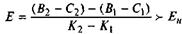(3.14)
где B1 и B2 — выручка по 1-му и 2-му вариантам вложений за год соответственно;
С1 и С2 — себестоимость годового объема производства продукции по 1-му и 2-му вариантам соответственно;
ЕН — норма сравнительной экономической эффективности дополнительных капитальных вложений.
Умножив обе части неравенства на величину — (К2 — К1), получим следующее выражение, которое будет отражать наше исходное условие о том, что более капиталоемкий вариант является выгоднее:
В2 — С2 — ЕНК2 > В1 — С1 — EHK1
Заменим — В1 = N1 ц1 и В2 = N2 ц2
где N1 и N2 — годовые объемы производства продукции по 1-му и 2-му вариантам соответственно;
ц1 и ц2 — цены реализации единицы продукции по 1-му и 2-му вариантам соответственно.
После подстановки в исходное условие получим
Н2ц2 - (С2 - ЕНК2) > Н1ц1 - (С1 - ЕНК1) (3.15)
Вынесем в правой и левой частях неравенства годовой объем производства за квадратные скобки:
Н2 [ц2 - (c2 - ЕНК2y)] > Н1[ц1 - (c1 - ЕНК1y)] (3.16)
где C1 и C2 — себестоимость единицы продукции по 1-му и 2-му вариантам вложений (С1 = N1c1 и С2 = N2c2) соответственно;
К1у и К2у — удельные капитальные вложения на единицу продукции по 1-му и 2-му вариантам (К1y = К1 : N1 и К2у = К2 : N2) соответственно.
Исходя из условия выгодности более капиталоемкого варианта левая часть выражения (3.16) больше правой части. Обобщив представленное выражение, получим критерий сравнительной экономической эффективности дополнительных капитальных вложений:
Эп = N [ц - (с + ЕнКу)] _ max, (3.17)
где Эп — показатель приведенного эффекта, который выступает в качестве критерия сравнительной экономической эффективности дополнительных капитальных вложений.
В соответствии с требованием данного критерия из всех альтернативных вариантов вложений к внедрению следует принимать тот из них, у которого приведенный эффект окажется наибольшим. Причем данный критерий полностью устраняет первые три условия, которые надо обязательно выдерживать, чтобы им можно было пользоваться для поиска наилучшего варианта. В рассматриваемом критерии могут отличаться по вариантам и объемы производства продукции, и качество продукции. Кроме того, величина этого критерия должна быть строго больше нуля, что позволяет одновременно учесть третье условие о выдерживании абсолютной оценки эффективности вариантов проекта.
Рассмотрим конкретный пример расчета сравнительной экономической эффективности вариантов проекта и отбора лучшего из них. Предположим, что имеется три варианта технологического процесса, которые отличаются количеством выпускаемой продукции, качеством готовых товаров, а также текущими и капитальными затратами. Нормативный коэффициент сравнительной экономической эффективности дополнительных капитальных вложений составляет — Ен = 0,25.
| Вариант 1-й | Вариант 2-й | Вариант 3-й |
| N1 = 16 800 изд./год | N2 = 14 000 изд./год | N3 = 15 400 изд./год |
| ц1 = 21,4 руб./изд. | ц2 = 20,8 руб./изд. | ц3 = 19,1 руб./изд. |
| с1 = 15,2 руб./изд. | с2 = 14,9 руб./изд. | с3. = 13,2 руб./изд. |
| Кy1 = 21,3 руб./изд. | Кy2= 19,3 руб./изд. | Ку3= 18,5 руб./изд. |
По представленным исходным данным произведем расчеты приведенного эффекта по всем сравниваемым вариантам (формула 3.17).
Эп1 = 16 800[21,4 - (15,2 + 0,25- 21,3)] = 14 700 руб./год
Эп2 = 14 000[20,8 - (14,9 + 0,25- 19,3)] = 15 050 руб./год
Эп3 = 15 400[19,1 - (13,2 + 0,25- 18,5)] = 19 635 руб./год
Из полученных результатов ясно, что самым выгодным оказался третий вариант, у которого наивысший приведенный эффект — 19 635 руб. за год эксплуатации. Такой результат обусловлен относительно низкими текущими и капитальными затратами на каждую единицу выпускаемой продукции.
Однако и критерий максимума приведенного эффекта в условиях рынка не является всеобъемлющим критерием; его использование ограничивается условиями от 4-го и далее. Вот почему при определении лучшего варианта в условиях рыночного хозяйствования, если не выдерживаются указанные условия на практике, следует применять систему показателей, разработанных мировой экономической наукой и апробированных на протяжении многих десятилетий экономической практикой.
Дата добавления: 2016-02-11; просмотров: 947;