Коэффициент сравнительной экономической эффективности капитальных вложений

Формула для исчисления себестоимости продукции в общем виде выглядит следующим образом:

С = 3 + М + а • К, (3.7)

где С — себестоимость годового объема производства продукции;

3 — затраты на заработную плату трудового коллектива со всеми начислениями за год;

М — затраты материальных и топливно-энергетических ресурсов, расходуемых на производство продукции за год;

К — капитальные вложения в основные производственные фонды предприятия;

а — годовая норма амортизации основных производственных фондов

Разложим представленную формулу на две составляющие

С = (З + М) + а • К

Затраты, стоящие в скобке, — это часть текущих затрат предприятия, которые с увеличением фондоемкости производства, с насыщением предприятия средствами механизации и автоматизации, с применением прогрессивной технологии имеют тенденцию к сокращению, т.е. это затраты, которые естественным образом сокращаются по мере роста технической вооруженности, механовооруженности и энерговооруженности труда. Другая составляющая формулы (3.7) отражает амортизационные отчисления с основных производственных фондов; по мере роста последних она увеличивается.

Описанная закономерность достаточно наглядно представлена на рис. 3.4.

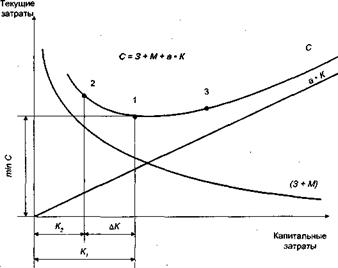
Рис. 3.4. Влияние капитальных затрат на величину себестоимости продукции

По оси Y откладываются текущие затраты на производство продукции (себестоимость), а по оси X — капитальные вложения в производство продукции.

Когда фондоемкость производства низкая и почти все производственные операции выполняются с помощью ручного труда, себестоимость продукции самая высокая. При этом капитальные вложения в основные производственные фонды незначительны.

По мере насыщения производственного процесса техникой, а, следовательно, и увеличения капитальных вложений в производство, происходит снижение себестоимости продукции. При этом закономерность снижения текущих затрат по мере возрастания вложений в производство будет выглядеть в виде гиперболической зависимости (кривая — З + М). Каждая последующая порция капитальных вложений будет приводить к снижению затрат на зарплату и материальные ресурсы, но при этом темпы такого снижения будут замедляться, так как резервы экономии указанных затрат постепенно сокращаются. Сами эти затраты, однако, не могут превратиться в ноль, сколько бы ни вкладывалось средств в развитие технической базы производства.

Совсем иначе ведет себя другая составляющая себестоимости — амортизационные затраты, которые возрастают прямо пропорционально капитальным вложениям в производство. На графике эти затраты представлены в виде прямой линии, исходящей из начала координат.

Если просуммировать обе составляющие себестоимости, то закономерность ее изменения по мере насыщения производства основными производственными фондами будет выглядеть в виде кривой, у которой вначале наблюдается падение текущих затрат до определенного уровня, а затем, пройдя точку перегиба, их возрастание.

Это и есть кривая изменения себестоимости продукции в зависимости от размера капитальных вложений в производство (кривая — С). Выделим на ней три точки — 1, 2 и 3. Точка 1 соответствует минимальному значению себестоимости выпускаемой продукции. В точках 2 и 3 себестоимость продукции выше, чем в точке 1. Но если себестоимость в точке 2 менее привлекательна, чем в точке 1, то капитальные затраты здесь представляют для инвестора определенный интерес. Вот почему точку 2 следует рассматривать как альтернативу точке 1, так как обе эти точки в чем-то взаимно уравновешивают друг друга (выигрыш в себестоимости и проигрыш в капитальных затратах и наоборот).

Совсем иначе обстоит дело с точкой 3. Она проигрывает точке 1 и в себестоимости, и в капитальных затратах, а потому не представляет интереса ни для предпринимателя, ни для инвестора. Таким образом, точку 1 следует рассматривать в качестве правой границы анализируемых вариантов эффективности капитальных вложений. Все точки, лежащие левее этой границы, могут представлять экономический интерес и должны включаться в сравнительный анализ для выбора лучшего из рассматриваемых вариантов.

Поэтому в дальнейшем будем рассматривать только две точки — 1 и 2. Точка 1 — единственная в своем роде, это пограничная точка эффективности вложений; точка 2 представляет собой любую возможную альтернативную точку, которая может оказаться более привлекательной, чем точка 1. Поэтому дальнейший теоретический анализ сравнительной эффективности вложений на примере двух указанных точек можно рассматривать как необходимый и достаточный.

Итак, первый вопрос, на решение которого нацелен анализ, заключается в том, чтобы определить, какой из рассматриваемых альтернативных вариантов более предпочтителен. Напомним при этом, что по всем остальным признакам варианты полностью удовлетворяют и предпринимателя, и инвестора.

Сравним оба рассматриваемых варианта. Итак, если внедрить первый вариант, то за год можно сэкономить на себестоимости продукции величину — (С₂ — С₁). Эта экономия, разумеется, сравнительная, так как она показывает, какой выигрыш получит предприниматель, отдав предпочтение первому варианту перед вторым. Однако здесь есть не только выигрыш, но и проигрыш: внедряя первый вариант, предприниматель несет более весомые капитальные затраты. И этот проигрыш можно точно подсчитать — (К₁ — К₂) или, как говорят экономисты, его внедрение потребует дополнительных капитальных вложений в размере — ∆К.

Теперь соизмерим полученную выгоду с дополнительными единовременными вложениями от внедрения первого варианта по сравнению со вторым:

(С₂ — С₁) : (К₁ — К₂).

Такое соотношение называется коэффициентом сравнительной экономической эффективности дополнительных капитальных вложений и записать его можно в следующем виде:

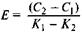(3.8)

где Е — величина искомого коэффициента эффективности;

С₁ и С₂ — соответственно себестоимость годового объема производства продукции в руб./год по 1-му и 2-му вариантам;

К₁ и К₂ — капиталовложения в 1-й и 2-й варианты соответственно.

Иногда вместо коэффициента эффективности определяют обратное ему выражение, которое представляет собой показатель срока окупаемости дополнительных капитальных затрат. Его величина рассчитывается по формуле

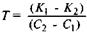(3.9)

где Т — срок окупаемости дополнительных капитальных вложений, лет.

Рассчитав показатель коэффициента эффективности по формуле (3.8) или срока окупаемости по формуле (3.9), еще невозможно ответить на вопрос, какой из двух рассматриваемых вариантов является наилучшим. Для этого необходимо сравнить полученные расчетные показатели с заранее установленным нормативом. Их обозначают соответственно Е_Н и Т_Н. Тогда условие выгодности более капиталоемкого варианта можно представить в виде следующих неравенств:

Е > Е_Н или Т < Т_Н (3. 10)

Указанные выражения можно записать иначе (это будут условия выгодности более капиталоемкого варианта по сравнению с менее капиталоемким из двух рассматриваемых и сопоставляемых между собой вариантов):

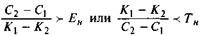(3.11)

В дальнейшем мы будем пользоваться первой из представленных формул, т.е. формулой коэффициента сравнительной эффективности дополнительных капитальных вложений.

Итак, пусть имеется два альтернативных варианта вложений. По 1-му варианту себестоимость производства продукции за год составляет — С₁ = 10 000 руб., а по 2-му — С₂= 12 000 руб. Потребность в капитальных вложениях будет соответственно равна - К₁ = 200 000 руб. и К₂ = 190 000 руб.

Тогда коэффициент эффективности по формуле (3.8) составит:

Е= 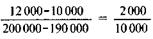=0,2

Полученная величина свидетельствует о том, что дополнительные капитальные вложения дадут отдачу в размере — 0,2 руб. экономического эффекта от снижения себестоимости продукции на каждый руб. дополнительных вложений. Хорошо это или плохо, какой из двух рассматриваемых вариантов лучше отсюда еще не ясно. Прежде чем ответить на этот вопрос, рассмотрим норматив эффективности; пусть он будет — Е_Н = 0,15. Тогда согласно формуле (3.11) можно утверждать, что предпочтительным является более капиталоемкий вариант, т.е. 1-й вариант, так как в соответствии с формулой (3.10) имеем, что 0,2 > 0,15. Если норматив принять на уровне — Е_Н = 0,25, более выгодным становится менее капиталоемкий вариант, 2-й вариант.

Таким образом, при выборе лучшего варианта из двух рассматриваемых важную роль играет величина принятого норматива эффективности дополнительных вложений, т.е. норма — Е_Н.

В условиях рыночной системы централизованные нормативы уже не действуют, и каждая фирма сама устанавливает для себя его значение.

Ответить на вопрос о том, чем руководствуются фирмы при определении величины норматива эффективности дополнительных капитальных вложений, практически невозможно. У каждой из них могут быть в каждый данный момент свои особые проблемы, свои возможности, свои потребности в капитальных вложениях, свои свободные денежные ресурсы, и, наконец, просто свои представления о том, какой должна быть норма эффективности вложений.

Тем не менее все они учитывают некоторую рекомендацию при установлении для себя нормы эффективности капитальных вложений, а именно чистые дивиденды, которые выплачивает на вложенные денежные средства по годовому депозиту высоконадежный коммерческий банк. Данная рекомендация исходит из того, что у предпринимателя есть альтернатива несколько иначе использовать свободные денежные ресурсы, получая гарантированный доход от их вложения на один год в указанный банк. Вот этот доход и будет принят предпринимателем в качестве нормы эффективности вложений свободных денежных ресурсов.

Можно вложить деньги в конкретный проект, который при его реализации принесет на каждый рубль капитальных затрат эффект на экономии текущих затрат, скажем, 0,3 руб. Однако можно не вкладывать свободные деньги в проект, а положить их в банк, где можно гарантированно получать на внесенные деньги чистые дивиденды в размере, скажем, 0,2 руб. Следовательно, последняя цифра и будет тем самым ориентиром, с которым предприниматель будет сопоставлять свои возможные Доходы от реализации проектного решения. Если получаемые от проекта доходы будут больше, чем он может получить в банке, то следует, очевидно, вкладывать деньги в реализацию проекта. Когда доход от проекта меньше, чем гарантирует банк, то лучше вкладывать деньги именно в банковский депозит. Таким образом, гарантированный дивиденд и есть тот самый норматив эффективности дополнительных капитальных вложений, который в первом приближении может принять фирма для решения своих предпринимательских задач в соответствии с условием формулы (3.11). Разумеется, каждая фирма может установить определенную поправку на величину такого норматива. Так, она может учесть риск вложений в проект, и тогда норма эффективности вложений несколько возрастет. Здесь также можно порекомендовать формулу для определения величины указанного норматива:

Е_Н = Е_Г+ Е_Р + Е_П, (3.12)

где Е_Н — норматив сравнительной экономической эффективности дополнительных капитальных вложений;

Е_Г — гарантированная норма доходности вложений в высоконадежный коммерческий банк;

Е_Р — дополнительная страховая норма, учитывающая риск вложений в проект (эта норма должна учитывать страхование проектной деятельности и от полноты страховки норматив будет либо равен нулю, либо примет весьма значительные размеры);

Е_П — минимальная предельная норма доходности вложений, которая принимается предпринимателем для положительного решения о дополнительных вложениях в реализацию отобранного варианта проекта.

По экономической сущности последнее слагаемое формулы (3.12) и есть тот самый дополнительный эффект от снижения себестоимости продукции при реализации более капиталоемкого варианта, ради которого он и принимается к внедрению. Два первых слагаемых при этом играют роль воспроизведения гарантированного дохода от вложений денежных средств в высоконадежный банк.