Оценка облигации с фиксированной ставкой

Пусть r – ставка дисконта, r_k – купонная процентная ставка. Обладатель облигации каждый год до момента погашения облигации через n лет получает процентный платеж от номинальной стоимости F, равный .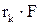

Тогда, текущая стоимость облигации равна:

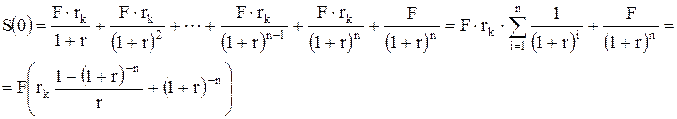(3.22)

Пример 44.

Оценить текущую стоимость облигации (PV) по номинальной стоимости

1 млн руб. с купонной ставкой r_k=16 %, дисконтом r=10 %. Срок погашения 5 лет.

Решение.

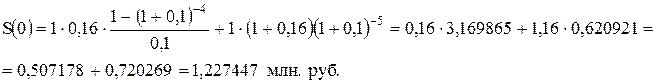
При оценке облигации на фондовом рынке часто используется эффективная процентная ставка купонной облигации. Предполагается что, известна курсовая стоимость облигации S(0), номинальной стоимости F, количество n платежей, размер 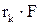. и время получения купонных платежей t₀, t₁, t₂, … t_n.

Финансовые операции с купонной облигацией описываются двухсторонний поток платежей C₀, C₁, C₂, … C_n в моменты времени t₀, t₁, t₂, … t_n , где

C₀ = - S(0), C_i = 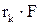(i = 1, 2, … n). Эффективная ставка r построенного потока платежей, называется эффективной ставкой купонной облигации. Она является решением уравнения (3.21).

Воспользуемся приведенной схемой для расчета эффективной ставки купонной облигацией на следующем примере:

Пример 45.

Оценить эффективную процентную ставку купонной облигации. Курсовая стоимость облигации PV = 330 тыс. руб. (370 тыс. руб.) по номинальной стоимости 300 тыс. руб. с купонной ставкой r_k=20 %. Срок погашения через 5 лет.

Решение.

Ежегодный купонный платеж равен 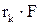=0,2*300=60 тыс. руб. Финансовой операции с данной купонной облигацией соответствует двухсторонний поток платежей:

1) при курсовой стоимости облигации PV = 330 тыс. руб.

-330, 60, 60, 60, 60, 360 (тыс. руб.);

1) при курсовой стоимости облигации PV = 370 тыс. руб.

-370, 60, 60, 60, 60, 360 (тыс. руб.).

Вычисления в Excel по программе ЧИСТВНДОХ() дают для первого случая эффективную процентную ставку 16,86 % для второго случая 13,3 %.