Оценка бессрочных облигаций с постоянным доходом
Для бессрочных купонных облигаций ежегодно выплачивается доход c и срок погашения отсутствует. Тогда текущая стоимость облигаций равна:
.
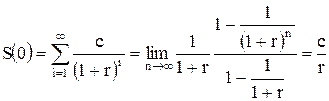Пример 46.
Оценить текущую стоимость бессрочной облигации, если по ней ежегодно выплачивается доход 10 тыс. руб. Ставка дисконта r=9 %.
Решение.
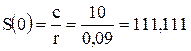тыс. руб.
Пример 47.
Какую сумму надо положить на счет инвестиционного фонда, чтобы ежемесячно получать 25 тыс. руб. Фонд инвестирует средства по ставке 12 % годовых.
Решение.
Месячная ставка равна r=1% (1/мес.), ежемесячные выплаты c=25 тыс. руб. Тогда, в инвестиционный фонд следует вложить:
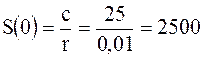тыс. руб.=2,5 млн. руб.
Оценка обыкновенных акций
Пусть D1, D2, ¼, Dn, ¼ – величина дивиденда, выплачиваемая за 1, 2, ¼,
n, ¼ период и r – ставка дисконта. Тогда курсовая цена акции равна ее текущему значению.
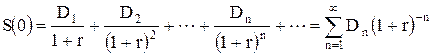. (3.23)
Постоянный дивиденд. Если дивиденды, выплачиваемые на одну акцию, постоянны и равны D, то стоимость акции равна:
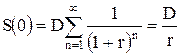. (3.24)
Пример 48.
Оценить текущую стоимость акции, если каждый год дивиденд равен 100 тыс. руб. Ставка дисконта r=10 %.
Решение.
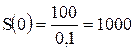тыс. руб.
Формула Гордона.
Оценим акции с равномерно возрастающими дивидендами. Пусть q – ставка, определяющая постоянный темп роста дивидендов и D – начальное значение дивиденда. Тогда, полученные дивиденды для 1, 2, ¼, n, ¼ года равны соответственно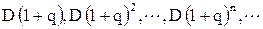 
.
Учитывая ставку дисконта r (r>q) для текущей стоимости акции получим формулу:
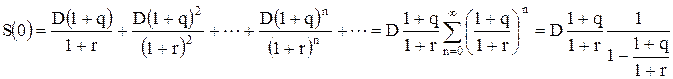Окончательно получаем формулу Гордона:
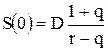. (3.25)
Пример 49.
Компания начальный дивиденд D=50 тыс. руб. ежегодно наращивает с темпом роста q=5 %. Найти текущую стоимость акций компании при ставке дисконта r=10 %.
Решение.
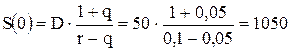тыс. руб.
Формула Модильяни
Пусть в начальный момент при t=0 капитал акционерного общества равен K, выпущено N простых акций. Процентная ставка равна r.
Тогда, доход акционерного общества равен Qt = a Kt-1.. Он зависит от капитала акционерного общества в предыдущий момент времени Kt-1 и показателя a эффективности работы акционерного общества (a>0).
Часть полученного дохода направляется на дивиденды:
dt = b Qt = a b Kt-1 
0<b<1 (3.26),
где b- определяет часть дохода, направляемую на дивиденды (0 < b < 1).
Остальной доход увеличивает капитал акционерного общества на величину:
∆t = Qt - dt = (1-b) Qt = a (1-b) Kt-1. (3.27)
Тогда, капитал в момент t будет равен:
Kt = Kt-1 + ∆t (3.28)
Подставляя формулу (3.27) в (3.28), получаем рекуррентную формулу для капитала:
Kt = (1+ a (1-b)) Kt-1 (3.29)
В начальный момент при t=0 капитал фирмы равен K. Тогда, через год капитал фирмы будет равен:
K1 = (1+ a (1-b)) K
Через 2 и 3 года капитал фирмы будет равен соответственно:
K2 = (1+ a (1-b)) K1 =(1+ a (1-b))2 K
K3 = (1+ a (1-b)) K2=(1+ a (1-b))3 K
Очевидно, что для капитала фирмы в момент времени t имеем:
Kt = (1+ a (1-b))t K (3.30)
Найдем теперь величину дивидендов на каждую акцию. Величина дивидендов на каждую акцию равна частному от деления общего объема средств dt, выделяемых на дивиденды (3.26) на количество акций N. При этом капитал вычисляется по формуле (3.30). Отсюда, дивиденды, выплачиваемые на одну акцию в момент t, будут равны:
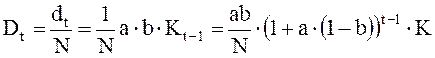(3.31)
Для оценки стоимости акций построим поток платежей (см. рис 3.9.)
S(0)
Рис 3.11.
Стоимость акции равна современной стоимости данного потока платежей при процентной ставке r. Следовательно, стоимость акции равна:
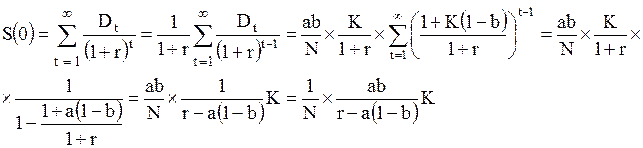
Окончательно формула Модильяни для оценки акций имеет вид:
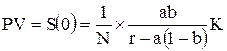,. (3.32)
где K- начальный капитал,
N - общее число обыкновенных акций,
a - коэффициент, характеризующий успешность работы акционерного общества,
b – коэффициент, определяющий долю доходов направляемых на дивиденды,
r - процентная ставка.
Пример 50.
Пусть начальный капитал акционерного общества составляет K=60 млн руб., коэффициент, характеризующий успешность работы акционерного общества равен a=10 %, доля доходов отправляемых на дивиденды составляет b=30 %, ставка дисконта равна r=12 %, а общее количество акций N=10 тыс.=104. Найти текущую стоимость акции компании.
Решение.
Воспользовавшись формулой (3.32) для текущей стоимости акции компании получим:
Дата добавления: 2016-03-15; просмотров: 2464;