Динамика поворота автомобиля на эластичных колесах

Общий случай

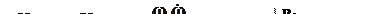
Рассмотрим два последовательных положения автомобиля через интервал времени Δt и спроецируем новые скорости на старые, затем вычтем старые: ;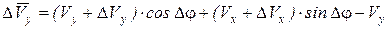

Т.к. Δtà0, то Δφà0 => cosΔφà1, sinΔφàΔφ, тогда получим

четвертым членом пренебрегаем и берем производную:

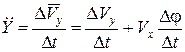à 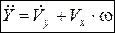– полное боковое ускорение.

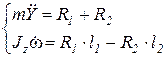– равновесие сил и моментов сил;

.

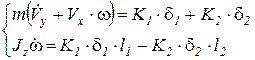Найдем δ_1,2 и R_1,2.

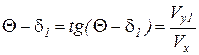, учитывая V_y1 = V_y + l₁ · ω получим

;

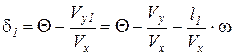учитывая V_y2 = l₁ · ω – V_y получим .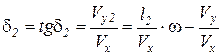

;

.

Теперь система уравнений примет вид:

перегруппируем уравнения:

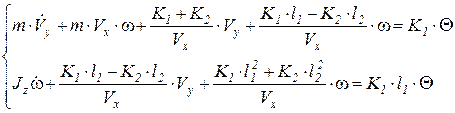
Разделим первое уравнение на m, а второе на J_z и сгруппируем первое:

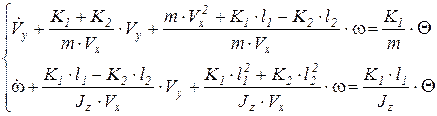
Введем коэффициенты а_1,2,3,4

; ;

; ;

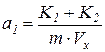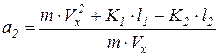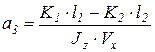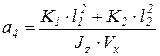общая система уравнений движения автомобиля.

При анализе динамики движения автомобиля рассматривают три основных процесса:

Ø Рывок руля

Θ = К_Θ · t,

Где К_Θ – коэффициент скорости поворота руля.

Ø Переставка.

Ø Синусоида
Θ = А_Θ · sin βt,

где А_Θ – амплитуда поворота колес, рад; β – частота поворота колес.

7.7.2. Частный случай: прямолинейное движение

При прямолинейном движении Θ = 0:

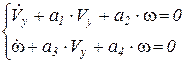
решение будем искать в виде V_y = A₁· e^ψt ω = A₂· e^ψt.

Учитывая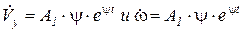

получим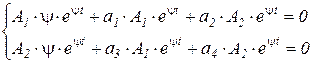

сократим e^ψt и сгруппируем:

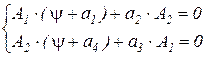à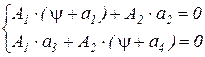

система имеет решение, если определитель равен нулю:

D = (a₁+ψ) · (a₄+ψ) – a₂ · a₃ = 0;

ψ² + (a₁ +a₄) · ψ +(a₁· a₄ – a₂ · a₃) = 0;

.

Движение устойчиво, если ψ<0.

(a₁ +a₄) всегда больше 0, следовательно, движение устойчиво, если корень меньше первого члена.

Решение существует, если неотрицательно подкоренное выражение и оно было бы минимальным.Для этого (a₁· a₄ – a₂ · a₃)>0.

Условие устойчивости: (a₁· a₄ – a₂ · a₃) = 0.

Еще раз запишем:

; ;

; ;

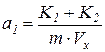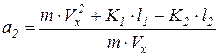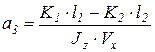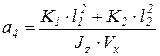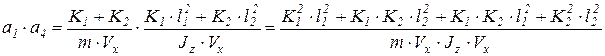
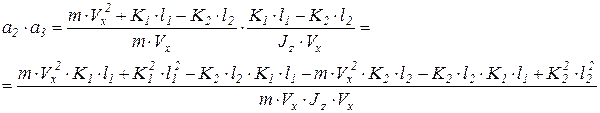
тогда

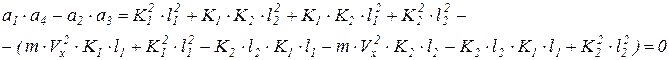
Сократим и сгруппируем:

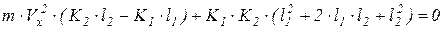
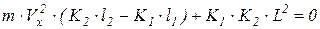поделим на К₁·К₂·L:

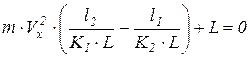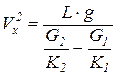à à – такое же выражение было получено и ранее.