Динамика поворота автомобиля на жестких колесах

Найдем боковые силы (реакции R_y1,2), действующие на каждую ось.

Рассмотрим «велосипедную» схему.

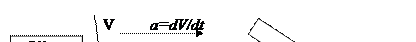Поворот ц.м. автомобиля можно представить в виде суммы двух поворотов относительно О` со скоростью ω и относительно О`` также со скоростью ω:

a` = V²/R.

V`` = ω · L₂;

а``=dV``/dt = d(ωL₂)/dt.

Т.к. ω =V/R= V·tgΘ/L.

Найдем производную произведения:

.

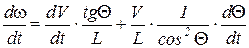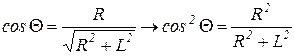
Тогда .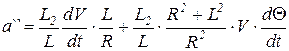

Полное боковое ускорение .

Боковая сила F_y = m · a_y.

Реакции на передней и задней оси зависят от распределения боковой силы и момента инерции автомобиля:

; ,

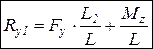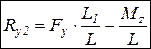где M_z = J_z dω/dt.

Для увеличения боковой устойчивости автомобиля необходимо в первую очередь снизить боковую нагрузку на заднюю ось, один из вариантов уменьшения боковой нагрузки на задней оси R₂ – увеличение момент инерции автомобиля J_z.

Динамика поворота автомобиля на эластичных колесах

Силовой увод шины

Под воздействием боковой силы F_y беговая дорожка колеса деформируется – образуется угол наклона беговой дорожки α.

Если на вращающее колесо начнет действовать боковая сила, то вектор скорости колеса отклонится от первоначального на некий угол δ – угол силового увода (угол между линией пересечения плоскости вращения колеса с дорогой и вектором скорости колеса):

Пояснение к схеме:

Ø т. А – Беговая дорожка только вошла в контакт с дорогой и пока не деформирована;

Ø т. В – середина контакта беговая дорожка деформирована на некоторую величину;

Ø т. С – конец зоны контакта – максимальная деформация беговой дорожки.

Увод колеса с эластичной шиной зависит от боковой силы:

1 – зона чистого увода – сила пропорциональна углу увода

2 – зона увода со скольжением

3 – зона чистого скольжения (занос):

F_y = F_ymax= R_z·φ_y

Вторая зона крайне не устойчивая, поэтому ею часто пренебрегают.

В зоне чистого увода вводят коэффициент сопротивления уводу:

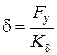[рад] è 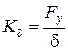[Н/рад].

Пример: шина 6,45 – 13 К_δ = 36000 Н/рад.

При нормальных условиях (ведомый режим при паспортной (номальной) вертикальной нагрузке) задают К_δн.

В очень большом приближении только при отсутствии опытных данных К_δн допустимо определять:

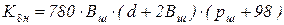– для радиальных шин;

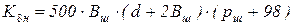– для диагональных шин,

где р_ш – давление в шине, кПа; В_ш – ширина профиля шины, м; d – посадочный диаметр шины, м.

Коэффициент сопротивления уводу К_δ зависит от:

Ø конструкции шины (радиальная жестче диагональной);

Ø давления в шине: с увеличением давления растет К_δ;

Ø продольной реакции R_x:

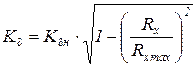
т.к. R_{x max} = R_z · φ_x, то .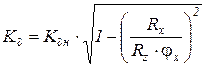

или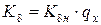

R_х = 0,20 · R_{х max} à К_δ = 0,979·К_δ0

R_х = 0,40 · R_{х max} à К_δ = 0,916·К_δ0

R_х = 0,60 · R_{х max} à К_δ = 0,800·К_δ0

R_х = 0,80 · R_{х max} à К_δ = 0,600·К_δ0

Ø нормальной реакции R по Литвинову:

R_z = – 20 % à К_δ = 0,973·К_δн

R_z = + 20 % à К_δ = 0,979·К_δн

R_zн – номинальная нагрузка на колесо.

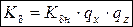
Выводы:

1. Колесо в ведущем режиме имеет К_δ меньше, чем в ведомом.

2. При номинальной вертикальной нагрузке колесо имеет максимальный коэффициент сопротивления уводу.

3. Коэффициент сопротивления уводу оси в целом равен сумме коэффициентов сопротивления силовому уводу колес:
– силовой увод оси (только за счет эластичности шин).

4. Коэффициент сопротивления силовому уводу оси всегда уменьшается при крене кузова. Уменьшение тем существеннее, чем больше угловая жесткость подвески.

Пример:

R_z1н = 5200 Н; R_z1в =2050 Н; R_zн =3625 Н; К_δн =31500 Н/рад; R_x`= 148 Н;R_x``=75 Н.

;

;

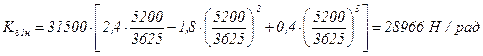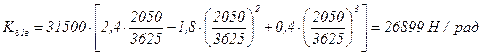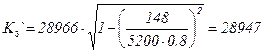Н/рад;

Н/рад.

.

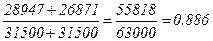Коэффициент сопротивления силовому уводу двух колес уменьшается на 11,4 %. (и это всего-то в ведомом режиме!!! В ведущем или тормозном режиме снижение К_δ существенно больше.