Стратегия поиска в глубину

Определим глубину вершины в дереве поиска следующим образом:

Глубина корня дерева равна 0.

Глубина вершины х, не являющейся корнем, равна глубине верши­ны у, такой, что x Î Г(y), сложенной с единицей.

В стратегии поиска в глубину каждый раз раскрывается вершина, глубина которой максимальна. Опишем алгоритм, реализующий стра­тегию поиска в глубину:

(1) Поместить начальную вершину в список, называемый ОТ­КРЫТ.

(2) Если список ОТКРЫТ пуст, то неудача всего алгоритма, иначе следующий шаг.

(3) В списке ОТКРЫТ взять вершину a с максимальным значением глубины и пронести ее в список ЗАКРЫТ.

(4) Если глубина a равна граничной глубине, то перейти к п. (2), иначе - следующий шаг.

(5) Раскрыть вершину a. Поместить каждую вершину b Î Г(a) в список ОТКРЫТ, если b не принадлежит ни списку ОТКРЫТ, ни списку ЗАКРЫТ.

(6) Если в Г(a) есть целевая вершина, то конец, иначе перейти к п. (2).

Для иллюстрации стратегии поиска в глубину обратимся к задаче отыскания маршрута, связывающего произвольные две вершины в графе. Рассмотрим граф, показанный на рис. 3.7. Пусть требуется найти маршрут, ведущий из вершины 1 в вершину 7. Начальная вершина 1 образует исходный список ОТКРЫТ = {1}.

Далее находим:

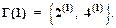
В скобках рядом с номером вершины помечено значение глубины вершины в графе. Полагаем ОТКРЫТ = 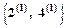, ЗАКРЫТ = .

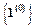Выбираем для раскрытия вершину 2:

Г(2) = {3,4,6}.

Поскольку вершина 4 уже фигурирует в списке ЗАКРЫТ, то уста­навливаем:

ОТКРЫТ = {4⁽¹⁾, 3⁽²⁾, 6⁽²⁾}; ЗАКРЫТ = {1⁽⁰⁾, 2⁽¹⁾}.

Выбираем в списке ОТКРЫТ вершину с максимальной глубиной, например, 3, и находим

Г(3) = {4}.

Вершина 4 не включается в список ОТКРЫТ, т.к. она там присут­ствует. Устанавливаем

ОТКРЫТ = {4⁽¹⁾, 6⁽²⁾}; ЗАКРЫТ = {1⁽⁰⁾, 2⁽¹⁾, 3⁽²⁾}.

Выбираем для раскрытия вершину 6:

Г(6) ={1, 5}

Полагаем

ОТКРЫТ = {1⁽¹⁾, 5⁽³⁾}; ЗАКРЫТ={1⁽⁰⁾, 2⁽¹⁾, 3⁽²⁾, 6⁽²⁾}.

Далее аналогичнонаходим

Г(5) = {3, 8};

ОТКРЫТ = {4⁽¹⁾, 8⁽⁴⁾};

ЗАКРЫТ = {1⁽⁰⁾, 2⁽¹⁾, 3⁽²⁾, 5⁽³⁾, 6⁽²⁾}.

Г(8) = {6, 9}

ОТКРЫТ = {4⁽¹⁾, 9⁽⁵⁾};

ЗАКРЫТ = {1⁽⁰⁾, 2⁽¹⁾, 3⁽²⁾, 5⁽³⁾, 6⁽²⁾, 8⁽⁴⁾}.

Наконец, Г(9) = {7}: Конечная вершина достигнута. Искомый маршрут определяется в обратном порядке через множества Г(a). Так, конечная вершина 7 принадлежит Г(9). Следовательно, вершина 9 долж­на быть предпоследней вершиной маршрута. Устанавливаем, что 9ÎГ(8). Таким образом, вершина 8 должна предшествовать вершине 9 и т.д. Окончательный список вершин, образующий маршрут из вершины 1 в вершину 7 таков: <1, 2, 6, 5, 8, 9, 7> (рис.3.8).

Рассмотренный алгоритм не использует каких-либо дополнительных предположений относительно свойств вершин - состояний. В частности, например, знание некоторых свойств, которыми должна обладать конечная вершина - состояние, позволило бы не раскрывать те вершины, которые в силу этих свойств не могут принадлежать результирующему маршруту (см. раздел 2.2). Это свойство используется различными стратегия­ми перебора с отсечениями.