Метод ветвей и границ
Метод ветвей и границ разработан Литлом, Мерти, Суини и Карелом. Рассмотрим основные идеи этого метода. Прежде всего, этот метод связан с некоторой общей схемой допущения и оценки альтернатив. Схема построения альтернативных предположений в общем виде может быть представлена, как это показано на рис. 3.9.
Вершины на рис. 3.9 соответствуют, как и ранее, состояниям задачи. Из каждой вершины выходит только два альтернативных направления, что, впрочем, не ограничивает общности рассмотрения. Направления отмечены буквами П с индексами. Идентификатор R(bi) есть некоторая числовая оценка, приписываемая вершине bi.
Вообще говоря, не имеется ограничений на глубину построения дерева, хотя ясно, что нужно стремиться к минимальной глубине. Этим, в частности, обосновывается выбор того или иного предположения Пm:сначала следует стремиться доказать предположение, достоверность которого в наибольшей степени сомнительна, или наоборот, попытаться опровергнуть предположение, достоверность которого в наибольшей степени правдоподобна, т.е. действовать по принципу reductio ad absurdum, поскольку вероятность получения противоречия здесь наибольшая, это позволяет отсечь соответствующую альтернативу у ее "истоков", вместо того, чтобы строить новые альтернативные предположения.
Пусть ищется состояние b*, в котором R(b*) минимально. Допустим далее, что известно некоторое текущее решение bx с текущим рекордом R(bx). Тогда ясно, что любое состояние bi, в котором наилучшее достижимое значение R(bi) ³ R(bx), может быть удалено (соответствующая часть дерева поиска отмечена, как показано с помощью заштрихованной области на рис. 3.9).

Рис. 3.9
Рассмотрим задачу коммивояжера в следующей частной постановке. Пусть дано множество N из 4 городов, соединенных дорогами. Будем интерпретировать N сетью, в которой вершины соответствуют городам, причем дугам, соединяющим вершины, приписаны веса сij, учитывающие затраты на переход коммивояжера из города i в город j (рис. 3.10а).
|
 Полагаем сij ³ 0 и сii = ¥ , причем необязательно, чтобы сij = сji. Будем кодировать задачу матрицей затрат С = [сij], показанной на рис. 3.10,б.
Полагаем сij ³ 0 и сii = ¥ , причем необязательно, чтобы сij = сji. Будем кодировать задачу матрицей затрат С = [сij], показанной на рис. 3.10,б.
А) б)
Рис. 3.10
В задаче коммивояжера требуется найти цикл с минимальной суммой затрат образующих его дуг, который обходит каждую вершину не более одного раза, за исключением одной вершины, из которой цикл "стартует" и в которой он же "заканчивается".
Рассмотрим решение этой задачи методом ветвей и границ. Решающими оказываются следующие два обстоятельства.
А1) Решению задачи коммивояжера соответствует выбор ровно одного элемента в каждой строке матрицы затрат С и ровно одного элемента в каждом столбце этой матрицы, причем сумма выбранных элементов минимальна и они образуют цикл. Последнее замечание существенно. Например, элементы (1, 2), (2, 3), (3, 1), (4, 4) не образуют цикл.
А2) Если из любой строки (столбца) вычесть (добавить) одну и ту же константу D, то результирующее значение С* суммарных затрат в оптимальном цикле Ц* уменьшится (увеличится) ровно на эту величину D.
Воспользуемся свойством А2. Выпишем минимальные элементы hj в каждом столбце j, после чего вычтем их из элементов соответствующих столбцов. Затем в полученной матрице выпишем минимальные элементы hi в строках i. Получим приведенную матрицу на рис. 2.11, а. Вычтем из каждой строки соответствующее значение hi (рис. 3.11, б).
Из матрицы на рис. 3.11, б легко устанавливается, что минимально возможное значение С* (которое обозначим 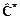 ) вычисляется следующим образом
) вычисляется следующим образом
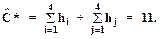
Теперь будем строить предположения для приведенной матрицы затрат на рис. 3.11, б.
Сделаем допущение, что дуга 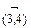 принадлежит Ц*; альтернативное допущение означает, что
принадлежит Ц*; альтернативное допущение означает, что 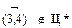 . Если дуга
. Если дуга 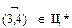 , то полагаем для дуги
, то полагаем для дуги 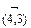 с4,3 = ¥, а также удаляем из матрицы затрат на рис. 2.11, б строку 3 и столбец 4, что в итоге дает матрицу, показанную на рис. 2.12, а. Приведенная матрица изображена на рис.2.12, б.
с4,3 = ¥, а также удаляем из матрицы затрат на рис. 2.11, б строку 3 и столбец 4, что в итоге дает матрицу, показанную на рис. 2.12, а. Приведенная матрица изображена на рис.2.12, б.
Для матрицы на рис. 2.12,б находим 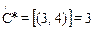 . Таким образом, получаем, что длина оптимального цикла, содержащего дугу
. Таким образом, получаем, что длина оптимального цикла, содержащего дугу 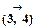 суть
суть
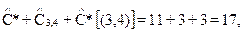
|
 определено из матрицы на рис. 2.12, б.
определено из матрицы на рис. 2.12, б.
| hi | hi | ||||||||||||
| ¥ | ¥ | ||||||||||||
| ¥ | ¥ | ||||||||||||
| ¥ | ¥ | ||||||||||||
| ¥ | ¥ | ||||||||||||
| hj | hj |
А) б)
Рис. 3.11
| hi | ||||||||||
| ¥ | ¥ | |||||||||
| ¥ | ¥ | |||||||||
| ¥ | ¥ | |||||||||
| hj | hj |
А) б)
Рис. 3.12
В то же время длина цикла 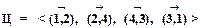 равна 5+2+3+2=12, следовательно, делаем вывод, что дуга
равна 5+2+3+2=12, следовательно, делаем вывод, что дуга 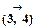 не входит в оптимальный цикл. Полагаем с3,4 = ¥.
не входит в оптимальный цикл. Полагаем с3,4 = ¥.
Допустим теперь, что дуга 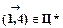 . Проведя аналогичные выкладки устанавливаем, что минимальная суммарная величина затрат для цикла, содержащего дугу
. Проведя аналогичные выкладки устанавливаем, что минимальная суммарная величина затрат для цикла, содержащего дугу 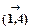 , составляет 13 единиц. Следовательно, это допущение также отбрасывается, т.к. оно не улучшает текущий рекорд. Полагаем с1,4 = ¥.
, составляет 13 единиц. Следовательно, это допущение также отбрасывается, т.к. оно не улучшает текущий рекорд. Полагаем с1,4 = ¥.
В результате в столбце 4 матрицы на рис. 3.10, б останется единственный допустимый элемент с2,4 = 2 . Полагаем,  . Это допущение позволяет удалить строку 2 и столбец 4. В результате получаем приведенную матрицу, изображенную на рис. 3.13, для которой Ц* равно 12.
. Это допущение позволяет удалить строку 2 и столбец 4. В результате получаем приведенную матрицу, изображенную на рис. 3.13, для которой Ц* равно 12.
Допустим, что дуга 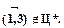 Тогда автоматически следует, что дуга
Тогда автоматически следует, что дуга 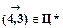 . Удалим строку 4 и столбец 3: получим приведенную матрицу, изображенную на рис. 3.14, из которой автоматически следует, что дуга
. Удалим строку 4 и столбец 3: получим приведенную матрицу, изображенную на рис. 3.14, из которой автоматически следует, что дуга 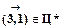 . Таким образом, из исходного предположения о том, что дуга
. Таким образом, из исходного предположения о том, что дуга  , устанавливаем следующий оптимальный цикл, не содержащий дуги
, устанавливаем следующий оптимальный цикл, не содержащий дуги 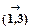 :
:
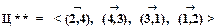
с суммарными затратами, равными 2 + 3 + 2 + 5 = 12.
| hi | hi | ||||||||||||||
| ¥ | |||||||||||||||
| ¥ | ¥ | ||||||||||||||
| hj | |||||||||||||||
| hj |
Рис. 3.13 Рис. 3.14 Рис. 3.15
Проверим теперь другую альтернативу: 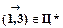 . Из этого допущения получим приведенную матрицу, изображенную на рис. 3.15. Непосредственно устанавливаем из рис.3.11, б и 2.15, что оптимальный цикл, содержащий дугу
. Из этого допущения получим приведенную матрицу, изображенную на рис. 3.15. Непосредственно устанавливаем из рис.3.11, б и 2.15, что оптимальный цикл, содержащий дугу 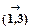 , имеет минимально возможные суммарные затраты, равные
, имеет минимально возможные суммарные затраты, равные
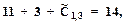
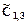 определяется ич матрицы на рис. 3.13.
определяется ич матрицы на рис. 3.13.
Таким образом, эта альтернатива отсекается, и мы получаем оптимальный цикл
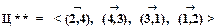 ,
,
суммарной величиной затрат, равной 12. Дерево поиска, которое было построено в ходе решения задачи, изображено на рис. 3.16.

Рис. 3.16
Символом “Х” обозначены отсекаемые направления, раскрытие которых гарантированно не улучшает рекорд. Отметим, что в этой задаче был сразу использован в качестве текущего рекорда оптимальный цикл, что, впрочем не снижает общности рассуждений, однако сокращает размеры построения дерева решения.
Дата добавления: 2016-03-05; просмотров: 883;

