Специфика решения задач в СИИ
Особенности задач, решаемых в СИИ, в значительной мере определяют выбор методов и подходов к решению задач в СИИ. Следующие особенности отличают задачи с технологией решения, ориентированной на СИИ:
(1) модель может быть частично определенной;
(2) критерий, как правило, отсутствует;
(3) решающая процедура основана на так называемых слабых методах;
(4) доказательство отсутствует.
Частичная определенность модели связана с недостаточными знаниями о предметной области (слабо или средне документированные предметные области). Для некоторых задач это свойство является характерным. Например, это относится к задачам логического вывода, а также комбинаторным оптимизационным задачам, с которыми приходится иметь дело при проектировании сложных систем, в частности. Кроме того, некоторые знания не формализуемы или плохо формализуемы (слабо или средне структурированные предметные области). В частично определенных моделях пространство состояний задачи не полно, в силу чего заключения СИИ носят предположительный или рекомендательный характер.
Наличие критерия свойственно вычислительным и оптимизационным задачам, для которых существует богатый арсенал математических детерминированных методов. Возможность использования точного математического алгоритма вообще не требует помощи эксперта, исключая, разве что, выбор самого алгоритма на основании анализа свойств задачи. Как правило, наличие критерия и строгая формализованность модели взаимосвязаны.
Важным аспектом, характерным для задач ориентированных на технологию СИИ, является использование слабых методов. К ним относятся:
- ограниченный направленный перебор;
- исключение и отсечение;
- эвристики;
- индукция.
Механизм логического вывода является в той или иной мере, разновидностью стратегии направленного перебора. При этом проблема заключается либо в выборе подходящей продукции на каждом шаге вывода из некоторого множества альтернативных продукций, для которых выполняются часть "ЕСЛИ ..." в текущем состоянии задачи, либо в выборе новой подцели (как, например, в языке Пролог). В первом случае вывод называется управляемым данными,во втором - управляемым, исходя из цели.Более подробно эти варианты вывода рассмотрены ниже.
Исключение (отсечение) - это эффективный механизм сокращения области поиска. Если решение не обладает свойством Р, то все варианты, которые устанавливают Р или вытекают из него, отбрасываются. Иначе говоря, если
W ® Р,
где ® - импликация, W - частное решение, Р - свойство искомого решения, то W отбрасывается равно как и любое другое решение U, логически предполагающее W. Отметим, что если
P ® W,
то отсечение в этом случае является лишь правдоподобным.
Наиболее интересная реализация механизма отсечения связана с построением предложений. Справедливо следующее правило:
"Снятие" некоторого условия задачи порождает альтернативы, а "допущение" условия - их снимает.
Всегда нужно искать такие условия, "снятие" которых порождает минимум альтернатив, а "допущение" - устраняет максимум альтернатив. Как следует из теоремы дедукции, гипотеза принимается, если принятие обратной гипотезы ведет к противоречию.
Пусть F - множество условий задачи. Пусть f - дополнительные условия и {FÈf} - условия для некоторой частной задачи, решение R которой найдено. Это решение будет решением исходной задачи, если F |¾ f, где |¾ - символ операции выводимости. Решение R можно считать опорным, если
(F |¾ f) &( F |¾ 
),
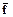т.е. из F не следует ни f, ни .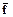
Опорное решение может не быть оптимальным, но оно не противоречит условиям задачи. Эффективная стратегия отсечения базируется на введении взаимоисключающих условий f и .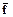
Пусть F - множество условий задачи. Если, например, допущение f ведет к противоречию (F, {f} |¾ ), то автоматически предполагается 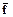и наоборот. При этом рациональным вариантом отсечения является допущение такой альтернативы, которая наиболее вероятно не имеет места (на этом, в частности, основывается идея доказательства от противного).
Эвристики.В сущности, эвристика - это эмпирическое правило, эффективность которого достаточна, чтобы применять это правило на практике. Значительная часть экспертных знаний представляют эвристики. Эвристика, например, используется для выбора продукции из множества альтернативных продукций. Формальный механизм организации эвристического поиска известен под названием Алгоритма А* Нильсона.
Индукция.Следующая логическая схема иллюстрирует механизм индукции
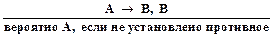(3.2)
Эта индукционная схема устанавливает, что если из формулы А следует В и имеет место В, то вероятно справедлива формула А, если не установлено противное.
Рассмотрим более детально связь методов решения задач в СИИ с классами задач, на которые они ориентированы.
Класс 1:малое пространство поиска с надежными знаниями и данными. Для этого класса задач основным методом решения является исчерпывающий перебор. При исчерпывающем поиске максимальный размер пространства поиска зависит от времени, необходимого на просмотр одного решения. Если на просмотр одного решения тратится 25 мс., то 10! решений могут быть последовательно просмотрены за 24 ч. Такой размер пространства часто соответствует верхнему пределу для реальных задач при полном переборе.
Класс 2:малое пространство поиска с ненадежными знаниями. В этом случае используются методы последовательного анализа вариантов на диаграмме состояния задачи. Стержнем методов является теорема Байеса, другие вероятностные подходы, например, метод Вальда.
Класс 3:модель задачи изменяется во времени. Например, задачи планирования и предсказания требуют рассуждений о всех возможных будущих ситуациях или событиях. Методы этой группы образуют так называемое ситуационное исчисление. Основу ситуационного исчисления составляет математическая логика и ее современные варианты, например, временная логика.
Класс 4:большое пространство состояний. Основным подходом к решению задач такого типа является механизм отсечений, использующий порождение гипотез и их проверку. Ключевым моментом является выполнение отсечений на наиболее ранних этапах построения решения, что сокращает перебор и обеспечивает повышение эффективности поиска решения. Существуют различные стратегии, использующие отсечение: механизм эвристического поиска, метод ветвей и границ, принцип сжимающих отображений.
Класс 5:задачи, требующие выдвижение гипотез и правдоподобные рассуждения. Методы, используемые для решения этих задач, основаны на различных неклассических логиках: вероятностной, нечеткой, немонотонной, логики возможностей и др. Соответствующие теоретические основы таких логик рассмотрены в главе 3. В настоящей главе подробно рассматриваются основные методы, используемые при решении укачанных классов задач.
Дата добавления: 2016-03-05; просмотров: 912;