Обзор формальных моделей вычислений
Описанная выше алгебраическая модель СП является обобщением ряда известных моделей, среди которых отметим реляционную модель А.С. Клещева, К-системы В.Е. Кузнецова, реляционную модель S.Vere, и модель управляемой СП V.Georgeff.
Реляционная модель вычислений, предложенная А. С. Клещевым, в качестве языка описания использует язык исчисления предикатов первого порядка. Элементами множества состояний являются конституанты, которые представляют собой атомные формулы вида:
P(c1,…, ck),
где р — некоторый k-арный предикатный символ, a ci, с2, ..., сk — константы. Множество переходов между элементами множества состояний задаетсяс помощью теории Т в языке исчисления предикатов первого порядка L, каждое предложение которой содержит в точности один знак импликации.
Для каждого множества конституант S определим связанную с ним структуру Ms языка L с помощью следующих условий
- все ms имеют один и тот же счетный универсум;
- в Ms истинны те и только те конституанты, которые входят в S.
Через Mq будем обозначать структуру, соответствующую пустому множеству конституант. Пусть Т — множество предложений языка L вида
f®ψ,
где ф и ψ — конъюнкции конституант, S0 — конечное множество конституант такое, что 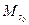 , не является моделью Т. Тогда процесс вычислений по программе Т над исходными данными S0 определяется следующим образом.
, не является моделью Т. Тогда процесс вычислений по программе Т над исходными данными S0 определяется следующим образом.
Для каждого ее a Î Т обозначим: na, wa — множества конституант, входящих в условие и в следствие а соответственно. Пусть на i-м шаге вычислено множество конституант Si такое, что S0 Í Si. Если некоторое a Î Т ложно в структуре 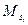 , то
, то
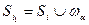 .
.
Выбор на i-ом шаге предложений a Î Т, ложных в структуре 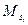 соответствует различному порядку выполнения действий при вычислениях.
соответствует различному порядку выполнения действий при вычислениях.
Процесс вычислений заканчивается, если для некоторого t структура 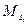 , — модель Т; St будем называть результатом вычисления.
, — модель Т; St будем называть результатом вычисления.
Аналогично определяется вывод в случае, когда в правилах языка используются переменные и кванторы, т.е. правила имеют вид "n1, …, nn(f®$u1, …, umy).
А..С. Клещевым исследована корректность вычислений в реляционной модели и доказано, что результат вычислений не зависит от порядка применения продукций. Эти исследования послужили теоретической основой для технологического комплекса СИНАП, успешно реализованного в ИАПУ ДВНЦ СССР.
Другой интересной формальной моделью СП являются К-системы, предложенные Кузнецовым В.Е.
Как уже было отмечено, одна из основных проблем при выводе в СП — это выбор соответствующих правил для применения. Замечено, что база продукций, представленная в виде сотен локальных правил, не описывает в явном виде отношение "общее-частное" над правилами. В К-системах введено отношение "общее-частное" над продукциями следующим образом: если q = {xi/ti} — подстановка, а р, q — продукции, и
p = qq,
где qq — это продукция, получаемая из q заменой всех вхождений переменных xi на ti то продукция р является частным случаем продукции q, а q — обобщение продукции р.
В К-системах введено несколько типов обобщений: подстановочное, категориальный синтез, отбрасывание посылок, исследованы свойства этих обобщений. На основании этих понятий вводится понятие исключение из правила.
Правило р является исключением из q (a q — общее правило по отношению к р), если область определения правила р является строго частным случаем области определения правила q. В К-системах реализована (встроена) следующая стратегия выбора правил: исключения всегда имеют больший приоритет чем общие правила. Данная стратегия близка к стратегии, реализованной в языке РЕФАЛ [З].
Предложенный подход оправдан с точки зрения здравого смысла и был успешно применен к задачам, связанным с синтаксическим анализом естественных языков.
Формальная модель СП, предложенная S.Vere [128], называется реляционной СП и определяется как пятерка
(C, V, L,s0 , P).
Здесь С — множество констант (обозначаемых строчными буквами); V - конечное множество символов переменных, принимающих значения в области констант (обозначаются заглавными буквами); L — множество литералов вида (е1 e2 ... еn) или Ø(e1 e2 . . . еn), п ³ 1, еi Î С È V; s0
— начальная ситуация, определяемая как конъюнкция литералов; Р — конечное множество правил вида
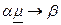 ,
,
где a — условие применимости (антецедент), b — следствие (консеквент), m — аспект (грань), a, b, m — конъюнкции литералов. Для того чтобы отделить аспект от антецедента, будем его подчеркивать в правилах.
Продукции предназначены для описания всевозможных преобразований исходной ситуации к некоторой ситуации s.
Продукция 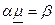 применима к ситуации s тогда и только тогда, когда aq Í s, где q — подходящая подстановка вида
применима к ситуации s тогда и только тогда, когда aq Í s, где q — подходящая подстановка вида
{t1/n1, …, tn/nn},
где ti — термы, ui — переменные.
Например, пусть s = (асе)(bес). Продукция (асХ)( 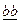 ) —> (саХ) применима к этой ситуации, так как
) —> (саХ) применима к этой ситуации, так как
(асе) = (acX){e/X},(ace) Î s.
Заметим, что в общем случае продукция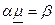 может применяться к ситуации несколькимиспособами, поскольку различные подстановки могут удовлетворять условиюa.
может применяться к ситуации несколькимиспособами, поскольку различные подстановки могут удовлетворять условиюa.
В дальнейшем конъюнкция литералов рассматривается как множество. Определим над нимитакие операции как объединение(È),пересечение(Ç),подмножество(Í)идополнение(—).
Если продукция р = 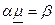 применима к ситуацииs, то рпреобразуетsв
применима к ситуацииs, то рпреобразуетsв
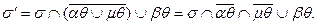
Будем говорить, что 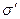 непосредственно выводимо из
непосредственно выводимо из 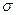 по продукции p.
по продукции p.
Рассмотрим пример. Если s = (ace)(bec), a
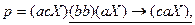
тогда 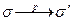 , где
, где
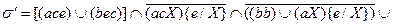
(caX){e/X} = (cae)(bec)
Основное направление исследований в рамках регуляционных моделей состоит в определении синтаксических условий вложенности регуляционных систем друг в друга и возможности декомпозиции регуляционной системы продукций на независимые подсистемы.
Все описанные модели описываются как частные случаи предложенной алгебраической модели.
Исследование формальных моделей сопровождалось проведением серии экспериментов по созданию прикладных систем продукций для предметных различных областей.
Дата добавления: 2016-03-05; просмотров: 744;
