Язык управления применением продукций

Описание процедур разрешения конфликта сводится обычно к заданию порядка применения продукций, называемому иногда дисциплиной при­менения. При этом порядок может быть либо детерминированным, когда на каждом шаге задается ровно одна продукция, либо недетерминиро­ванным, когда проверяются условия нескольких продукций, но их число значительно меньше общего количества правил в системе.

По способу задания можно выделить встроенный и настраиваемый порядки применения продукций. К встроенным относятся средства, ко­торые непосредственно запрограммированы в интерпретаторе системы. Примером встроенного порядка применения правил может служить схе­ма выбора правил в нормальных алгоритмах Маркова. На каждом шаге вывода проверяются условия только одного правила (на первом ша­ге — первого), если оно не применимо, то происходит переход к следую­щему. Если оно применилось, то на следующем шаге снова проверяются условия первого правила и т.д. В системе продукции можно упорядочивать по частоте использования или по самым длинным спискам условий, по приоритету и т.п. Кроме этого, в различных системах широко использовалось введение меток и тегов, специальных логических символов внутри продукции для задания последовательности выбора. Такие средства управления порядком применения продукций ак­тивно использовались в начальный период конструирования СП, когда под каждую процедуру разрешения конфликта программировался свой интерпретатор. Позднее эти средства подверглись острой критике мно­гими авторами, поскольку их введение означало отход от идеологии СП к традиционным средствам программирования. Это послужило толчком к развитию настраиваемых средств управления.

Первой попыткой в этом направлении было использование в систе­ме HEARSAY-II разбиения правил на подсистемы таким образом, чтобы в каждый момент времени рассматривалось лишь их приемлемое чис­ло [90]. Другим средством задания порядка являются метапродукции, использованные в комплексе систем MYCIN-TEIRESIAS [84]. Однако по­следовательность управляющей информации невозможно описать одни­ми метапродукциями (необходимо введение метаметапродукций и т.д.). По существу, идея введения метапродукций состоит в попытке задать всю возможную информацию в системе однородным образом.

Еще одним средством управления порядком применения правил явля­ется использование языков управления. Опишем неформально управля­ющие формулы и их использование при выводе.

Пусть Рr = {< q_i r_i >}, i = 1 ... n, п ³ 0 — множество продукций, d — текущее состояние базы данных. На языке управления порядком за­дается управляющая формула, описывающая множество продукций, для которых на текущем шаге вывода t проверяются условия применимости. Такие множества будем называть множествами активированных продукций a_r , a_r ÍРr.

Каждая продукция рr =< q,r > в задаваемом множестве может быть в одном из трех состояний:

- рr+ — условие продукции рr, активированной на шаге вывода t, должно быть истинно после проверки, т.е. найдется подстановка q такая, что qq Í d;

- рr- — условие продукции рr, активированной на шаге вывода t, должно быть ложно после проверки, т.е. не существует подстановки q такой, что qq Í d;

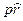- — продукция должна быть активирована, а значение ее условий (истинное или ложное) не влияет на переход к следующему шагу вывода.

Если, например, А_r = 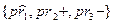, то переход к A_r+1 произой­дет в том случае, если условия рr₂ истинны, а рr₃ ложны. Истинность условий pr_i не влияет на переход к A_r+1. Требование ложности условий рr₁ является одним из средств задания отрицательного контекста, если он необходим при выводе.

Язык управления представляет собой множество правильно постро­енных формул {F} над состояниями продукций и бинарными операциями между ними, среди которых выделены следующие проверки условий: по­следовательная (•), одновременная (,) и альтернативная (;). Такие фор­мулы называются управляющими, а множество продукций с заданной на нем управляющей формулой — системой структурированных продукций.

Опишем неформально процесс вывода в Рr с управляющей формулой F на некотором шаге t. Для каждого шага вывода t по F формируется множество А_r, которое состоит из

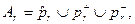
где

s) 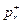— множество продукций, помеченных состоянием +, т.е. про­дукций, условия которых должны быть истинны на текущем шаге вывода r;

t) — множество продукций, помеченных состоянием -, т.е. продук­ций, условия которых должны быть ложны на шаге вывода r;

u) 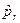— множество продукций, для которых не требуется однозначно­го ответа на вопрос, истинны ли их условия применимости на теку­щем шаге вывода, однако по мнению эксперта их разумно включить в число правил, у которых следует проверить условия применимо­сти, и если они истинны, то применить правила.

После проверки условий A_r распадается на два непересекающихся подмножества:

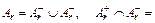Æ

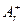где и 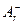множества всех активированных продукций с истинными и ложными условиями применимости соответственно.

Если выполнено условие , то применяются все продукции из множества 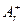и происходит переход к следующему шагу вывода. Вывод заканчивается успешно, если очередное A_r пусто. Если указанное условие не выполнено или A_r содержит специальный выделен­ный символ l, то вывода "зависает".

Как видно из неформального описания, введение средств управления позволяет сокращать число активируемых правил. Однако это возлагает большую ответственность на эксперта, поскольку выбранная им дисци­плина применения правил может оказаться неудачной.

Рассмотрим пример использования языка управления для решения задачи определения языка, порождаемого следующей формальной грам­матикой:

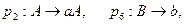
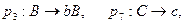
Приведенная контекстно-свободная грамматика порождает язык:

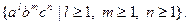
Введем над этой грамматикой управляющую формулу, которая описы­вается выражением

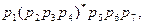
где ()* задает итеративное применение правил p2, p3 p4.

Данное выражение может быть изображено сетью переходов на рис.1.6

Рис. 1.6. Сеть переходов для языка управления

В результате использования управляющего языка множество слов будет представлять собой язык {aⁿbⁿcⁿ|n³1} , который не является контекстно - свободным.

Как видно даже из этого небольшого примера язык управления при­менением правил позволяет значительно упрощать основные продукции.