Теорема о циркуляци вектора напряженности магнитного поля
Ранее было показано (см. 9.1), что для поля в вакууме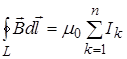 
.(10)
В случае поля в веществе эта теорема о циркуляции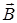 
запишется так
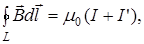(11)
где I и I’ соответственно алгебраические суммы макротоков и микротоков, охватываемых контуром L. Можно показать, что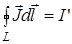 
. (12)
С учетом этого (11) перепишется в виде 
, (13)
или, принимая во внимание (7), найдем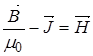 
и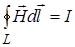 
, где I= 
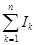- алгебраическая сумма макротоков.
В итоге имеем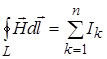 
. (14)
Выражение (14) представляет собой теорему о циркуляции вектора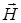 
и гласит: Циркуляция вектора напряженности магнитного поля 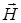по любому замкнутому контуру L равна алгебраической сумме макротоков, охватываемых контуром. Вектор напряженности магнитного поля 
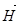, являясь аналогом электрического смещения 
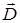, определяется только макротоками. Из (14) следует, что Н измеряется в А/ м.
Виды магнетиков
В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на три группы:
1) диамагнетики, у которых c отрицательна и мала 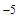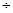(10 
10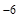 
); для них 
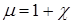несколько меньше единицы; диамагнетиками являются Zn, Au, Hg, Si, P, С (графит), Bi (висмут)... Диамагнетики незначительно ослабляют внешнее магнитное поле.
2) парамагнетики, у которых c положительна и мала 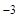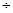(10 
10 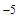); и с ростом температуры 
уменьшается по закону Кюри: c ~ 1/T, для них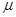 
несколько больше единицы; диамагнстиками являются щелочные металлы, кислород... Парамагнетики незначительно усиливают внешнее магнитное поле.
3) ферромагнетики, у которых c положительна и очень велика: может достигать, например, у супермалоя 800000; для Fe магнитная проницаемость 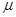= 5000. Таким образом, ферромагнетики являются сильномагнитными веществами.
m
|
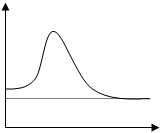
Рис. 2 Н
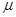для них зависит от H , (рис. 2) и для каждого ферромагнетика имеется определенная температура, называемая точкой Кюри, при которой он теряет магнитные свойства, т. к. области спонтанного намагничивания (домены) распадаются и ферромагнетик становится парамагнетиком - это фазовый переход II рода. Для железа 
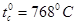или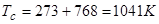 
.
Дата добавления: 2016-03-04; просмотров: 860;