Лекция 12. Основы теории Максвелла для электромагнитного поля

В 60-х годах прошлого века (около 1860 г.) Максвелл, основываясь на идеях Фарадея, обобщил законы электростатики и электромагнетизма: теорему Гаусса – Остроградского для электростатического поля 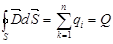и для магнитного поля 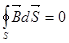; закон полного тока 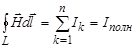; закон электромагнитной индукции 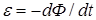, и в результате разработал законченную теорию электромагнитного поля.

Теория Максвелла явилась величайшим вкладом в развитие классической физики. Она позволила с единой точки зрения понять широкий крут явлений, начиная от электро­статического поля неподвижных зарядов и заканчивая электромагнитной природой света.

Математическим выражением теории Максвелла служат четыре уравнения Максвелла. которые принято записывать в двух формах: интегральной и дифференциальной. Дифференциальные уравнения получаются из интегральных с помощью двух теорем векторного анализа – теоремы Гаусса и теоремы Стокса. Теорема Гаусса:

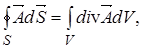(1)

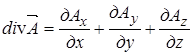(2)

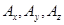- проекции вектора на оси; V - объем, ограниченный поверхностью S.

Теорема Стокса: . (3)

здесь rot - ротор вектора , который является вектором и выражается в декартовых коор­динатах следующим образом: 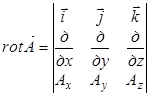, (4)

S - площадь, ограниченная контуром L.

Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей.

Уравнения Максвелла в дифференциальной форме показывают как связаны между собой характеристики электромагнитного поля и плотности зарядов и токов в каждой точке этого поля.

12.1. Первое уравнение Максвелла

Оно является обобщением закона электромагнитной индукции ,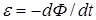

и в интегральной форме имеет следующий вид 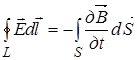(5)

и утверждает.что с переменным магнитным полем 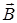неразрывно связано вихревое электри­ческое поле 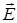, которое не зависит оттого находятся в нем проводники или нет. Из (3) следует, что 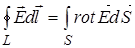. (6)

Из сравнения (5) и (6) находим, что 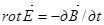(7)

Это и есть первое уравнение Максвелла в дифференциальной форме.

12.2. Ток смещения. Второе уравнение Максвелла

Максвелл обобщил закон полного тока 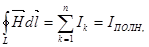предположив, что переменное электрическое поле, также как и электрический ток, является источником магнитно­го поля. Для количественной характеристики "магнитного действия" переменного электрического поля Максвелл ввел понятие тока смещения.

По теореме Гаусса - Остроградского поток электрического смещения сквозь замкну­тую поверхность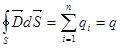

Продифференцировав это выражение по времени, получим для неподвижной и недеформирусмой поверхности S 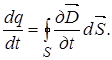(8)

Левая часть этой формулы имеет размерность тока, который, как известно, выражает­ся через вектор плотности тока 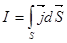. (9)

Из сравнения (8) и (9) следует, что 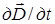имеет размерность плотности тока: А /м². Максвелл предложил назвать 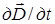плотностью тока смещения:

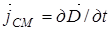. (10)

Ток смещения 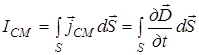. (11)

Из всех физических свойств, присущих действительному току (току проводимости), связанному с переносом зарядов, ток смещения обладает лишь одним: способностью соз­давать магнитное поле. При "протекании" тока смещения в вакууме или диэлектрике не вы­деляется тепло. Примером тока смещения может служить переменный ток через конденсатор. В общем случае токи проводимости и смещения не разделены в пространстве и мож­но говорить о полном токе, равном сумме токов проводимости и смещения: 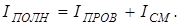(12)

С учетом этого Максвелл обобщил закон полного тока, добавив в правую часть его ток смещения . (13)

Итак, второе уравнение Максвелла в интегральной форме имеет вид:

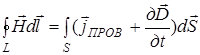. (14)

Из (3) следует, что 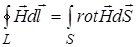. (15)

Из сравнения (14) и (15) находим, что . (16)

Это и есть второе уравнение Максвелла в дифференциальной форме.

12.3. Третье и четвертое уравнения Максвелла

Максвелл обобщил теорему Гаусса - Остроградского для электростатического поля. Он предположил, что эта теорема справедлива для любого электрического поля, как стационарного, так и переменного. Соответственно, третье уравнение Максвелла в интегральной форме имеет вид: 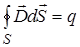. (I7) или . (18)

где 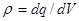- объемная плотность свободных зарядов, [ 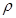]= Кл / м³

Из (1) следует, что 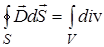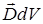. (19)

Из сравнения (18) и (19) находим,что 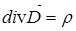. (20)

Четвертое уравнение Максвелла в интегральной и дифференциальной формах имеет

следующий вид: 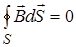, (21) 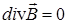. (22)

12.4. Полная система уравнений Максвелла в дифференциальной форме

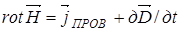. (23)

, .

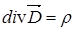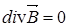Эту систему уравнений необходимо дополнить материальными уравнениями, характе­ризующими электрические и магнитные свойства среды:

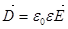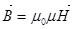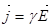, , . (24)

Итак, после открытия взаимосвязи между электрическими и магнитным полями ста­ло ясно, что эти поля не существуют обособлено, независимо одно от другого. Нельзя соз­дать переменное магнитное поле без того, чтобы одновременно в пространстве не возникло и электрическое поле.

Отметим, что покоящийся в некоторой системе отсчета электрический заряд создает только электростатическое поле в этой системе отсчета, но он будет создавать магнитное поле в системах отсчета, относительно которых он движется. То же самое относится и к неподвижно­му магниту. Заметим также, что уравнения Максвелла инвариантны к преобразованиям Лоренца: причем для инерциальных систем отсчета К и К’ выполняются следующие соотношения: 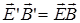, 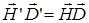. (25)

На основании изложенного можно сделать вывод, что электрические и магнитные поля являются проявлением единого поля, которое называют электромагнитным полем. Оно распространяется в виде электромагнитных волн