Построение диаграммы (графика, картины) частот вращения валов привода
Диаграмма частот вращения (ДЧВ) строится для выяснения действительных частот вращения валов коробки скоростей и действительных передаточных отношений групповых и одиночных передач. В отличие от структурных сеток ДЧВ, в общем случае, несимметрична. На ней лучи, отклоняющиеся от горизонтали вверх, изображают ускоряющие передачи, вниз - замедляющие. передачи 1:1 изображаются горизонтальными линиями.
Передаточное отношение передачи выражается в виде 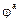 или 1/
или 1/ 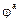 ,
,
где а – число интервалов между горизонталями, перекрытых лучом, изображающим данную передачу.
ДЧВ строится на весь привод, т.е. на групповые и одиночные передачи. При этом должны быть известны частоты вращения первого (электродвигатель) и последнего (шпиндель) валов:
nдв и 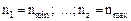 .
.
Отношение nmin/nдв является минимальным передаточным отношением привода. Выразим его через знаменатель геометрического ряда частот вращения шпинделя:
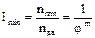 ,
,
где m – число интервалов между nmin и nдв на ДЧВ или по ряду предпочтительных чисел с принятым 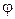 (см. табл. 3.6).
(см. табл. 3.6).
Число m может получиться целым или дробным. В последнем случае дробная часть принимается приближенно в несколько десятых, а погрешность от этого приближения устраняется далее при подсчете передаточного отношения какой-либо одиночной передачи.
Минимальное передаточное отношение Imin разбивают по групповым передачам. Остаток Imin распределяют между одиночными передачами.
При разбивке учитывают граничные условия для передач:
зубчатых – 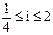 , ремённых –
, ремённых – 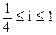 .
.
Разбивку Imin стараются вести так, чтобы было возможно меньше ускоряющих передач.
После разбивки минимальное передаточное отношение представляется на ДЧВ в виде так называемой линии редукции, на которой в соответствии с выбранной структурной сеткой достраиваются лучи, изображающие остальные передачи групп.
Пример. Построить ДЧВ привода с кинематической схемой по рис. 2.10, структура которого 12=3(1)·2(3)·2(6), частоты вращения шпинделя должны изменяться от nmin=33,5 об/мин до nmax=1500 об/мин, частота вращения вала электродвигателя nдв=1440 об/мин.
а) Определяем знаменатель ряда частот вращения шпинделя: 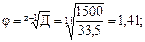
б) Выписываем из таблиц рядов предпочтительных чисел (см. табл. 3.6) для 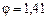 проектные значения частот вращения от nmin до nmax (или до nдв, если nдв>nmax):
проектные значения частот вращения от nmin до nmax (или до nдв, если nдв>nmax):
33,5 – 47,5 – 67 – 95 – 132 – 190 – 265 – 375 – 530 – 750 – 1060 – 1500;
в) проводим (рис. У.12) столько вертикальных линий, сколько валов в приводе (6: I, II, …, VI), и столько горизонтальных, сколько выписано частот вращения (12);
г) отмечаем на правой вертикальной линии – "валу VI" – точки, означающие частоты вращения шпинделя от nmin до nmax, а на левой линии – nдв;
д) определяем 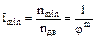 . Для этого подсчитываем m как число интервалов между nmin и nдв по таблице рядов предпочтительных чисел (см. табл. 3.6) или по ряду выписанных частот (см. п/п. б). От 33,5 до 1500 имеется 11 интервалов, а поскольку nдв=1440<1500, то примем приближённо m =10,9.
. Для этого подсчитываем m как число интервалов между nmin и nдв по таблице рядов предпочтительных чисел (см. табл. 3.6) или по ряду выписанных частот (см. п/п. б). От 33,5 до 1500 имеется 11 интервалов, а поскольку nдв=1440<1500, то примем приближённо m =10,9.
Минимальное передаточное отношение привода, таким образом, равно:
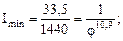
е) Рассмотрим все возможные варианты передаточных отношений в групповых передачах, исходя из граничных условий 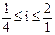 . Последнее при
. Последнее при 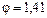 можно представить в виде:
можно представить в виде:
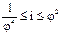 (т.к.
(т.к. 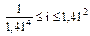 ).
).
Построим с этой целью ряд структурных графиков (рис. У.9; У.10; у,11):
а) б) в) г) д)
3(1)

| 1:φ2 | 1:φ | 1:1 | φ:1 | φ2:1 |
| 1:φ3 | 1:φ2 | 1:φ | 1:1 | φ:1 |
| 1:φ4 | 1:φ3 | 1:φ2 | 1:φ | 1:1 |
Рис. У.9. Структурные графики для группы "а" (ра=3) в качестве основной,
показывающие возможные комбинации передаточных отношений в группе
Сопоставляя возможные варианты передаточных отношений в каждой группе, выбираем те, которые обеспечили бы наилучшие условия для работы передач. В качестве таковых принимаем для групп pо, pI, pII варианты по рис. У.9,в, У.10,б, У.11. В них обеспечивается
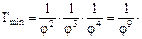
Примечание. При разбивке передаточного отношения φ можно принимать и в целых, и в дробных степенях. Но в последнем случае надо соблюдать некоторые условности, заключающиеся в следующем. Принимают дополнительно какое-либо φmin (1,015; 1,03 или 1,06) и должно выполняться условие φ±b= φmin±t, где b – число дробное, но t – число целое.
а) б) в) г) 2(6)
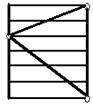 2(3)
2(3)
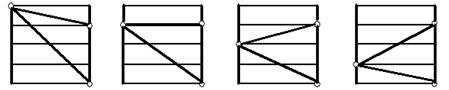
| 1:φ | 1:1 | φ:1 | φ2:1 | φ2:1 |
| 1:φ4 | 1:φ3 | 1:φ2 | 1:φ | 1:φ4 |
| Рис. У.10. Структурные графики для группы "б" (рб=2) в качестве I множительной, показывающие возможные комбинации передаточных отношений в группе | Рис. У.11. Структурный график для группы "в" (рв=2) в качестве II множительной |
ж) Т.к. 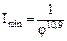 , то остаток передаточного отношения
, то остаток передаточного отношения 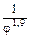 распределяем между одиночными передачами. Пусть
распределяем между одиночными передачами. Пусть 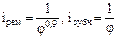 и тогда
и тогда 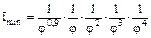 ;
;
з) Построим на заготовке для ДЧВ (см. рис. У.12) ветвь Imin – линию редукции. Затем, используя выбранные структурные графики или структурную сетку, достраиваем остальные лучи – передаточные отношения (см. рис. У.12);
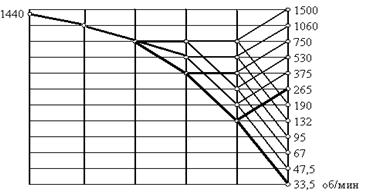
I II III IV V VI
Рис. У.12. Построение диаграммы частот вращения шпинделя
и) Определим диаметры шкивов ременной передачи, исходя из действительных частот вращения валов, связываемых данной передачей. Это позволит устранить погрешность, допущенную при определении m и Imin (см. п/п. д).
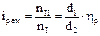 и
и 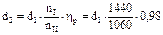 .
.
Приняв d1 =90 мм, получим d2 =120 мм.
Примечания.
1 Если применяется клиноремённая передача, то, приняв желаемое число ремней (чаще: 3-4), определяют по справочникам, ремни какого сечения (0, А, Б, …) при желаемом их числе суммарно обеспечат передачу полной мощности приводного электродвигателя. По этому сечению принимают минимальный расчётный диаметр меньшего шкива, например, для сечения 0 – диаметр 63, А – 90, Б – 125, В – 200 мм и т.д.
2 Если в приводе нет ременной передачи, то аналогичным образом, т.е. исходя из действительных частот вращения, подсчитываются числа зубьев колёс одиночной зубчатой передачи. К примеру, если в рассматриваемом приводе вместо ременной была бы зубчатая передача Z':Z", то можно было бы принять по передаточному отношению Z':Z"=1060:1440 различные варианты чисел зубьев, и в том числе 53:72; 35:48; 30:41 и т.п.
к) Из ДЧВ выписываем: 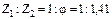 . По i=1:1,41 можно принять множество вариантов чисел зубьев колёс передачи, например 20:28, 25:35; 30:42; 35:49; 40:56 и т.д., которые будут в той или иной степени близки к заданному передаточному отношению;
. По i=1:1,41 можно принять множество вариантов чисел зубьев колёс передачи, например 20:28, 25:35; 30:42; 35:49; 40:56 и т.д., которые будут в той или иной степени близки к заданному передаточному отношению;
л) Из ДЧВ выписываем все передаточные отношения групповых передач
| валы III - IV – гр. "а" | валы IV - V – гр. "б" | валы V - VI – гр. "в" |
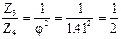
| 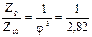
| 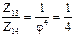
|
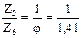
| 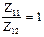
| 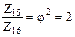
|
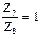
|
м) Далее определяются числа зубьев всех шестерён и на ДЧВ проставляются подсчитанные числа зубьев и диаметры шкивов. Также проставляются фактические (после подсчёта) частоты вращения валов.
Считается, что фактические значения частот вращения не должны превосходить стандартных значений более чем на ±10(φ–1) %.
Пример правильного оформления ДЧВ показан на рис. 3.8.
ДЧВ отражает всё то, что содержится в структурной сетке и кроме того показывает:
- количество одиночных передач и относительное расположение их среди групповых;
- передаточные отношения всех передач привода;
- частоты вращения валов при любых вариантах включения передач.
Выбор оптимального варианта ДЧВ
Разбивка Imin может быть произведена по-разному. ДЧВ при этом также будут различаться. Например, для привода на 6 вариантов с двумя одиночными зубчатыми передачами при φ=1,41 и Imin=1/φ10 возможно несколько ДЧВ, в том числе показанные на рис. 3.2. Чтобы проанализировать их, рассмотрим следующее.
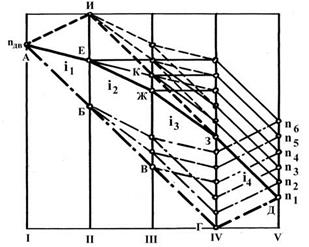 Рис. 3.2. К выбору оптимального варианта
диаграммы частот вращения
Рис. 3.2. К выбору оптимального варианта
диаграммы частот вращения
| 1) Крутящий момент, передаваемый шестерней, шкивом, муфтой, валом, обратно пропорционален частоте вращения:
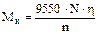 , Н×м,
где N – мощность привода в кВт;
η – КПД кинематической цепи от электродвигателя до рассматриваемого элемента привода;
n – частота его вращения, об/мин.
Поскольку модули шестерен (m), диаметры валов (d) и размеры других элементов привода находятся в прямой зависимости от крутящего момента (например, , Н×м,
где N – мощность привода в кВт;
η – КПД кинематической цепи от электродвигателя до рассматриваемого элемента привода;
n – частота его вращения, об/мин.
Поскольку модули шестерен (m), диаметры валов (d) и размеры других элементов привода находятся в прямой зависимости от крутящего момента (например, 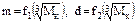 и т.д.), то снижение частот вращения элементов привода обуславливает возрастание их размеров.
В этом плане привод по ДЧВ с линией редукции АБВГД, имеющий сначала три предельно допустимые замедляющие передачи (передаточное и т.д.), то снижение частот вращения элементов привода обуславливает возрастание их размеров.
В этом плане привод по ДЧВ с линией редукции АБВГД, имеющий сначала три предельно допустимые замедляющие передачи (передаточное
|
отношение каждой – 1/4), а в конце – ускоряющую передачу с максимально возможным передаточным отношением (2), будет самым невыгодным.
Размеры элементов привода, а значит габариты и масса всего привода, могут получиться наименьшими при выборе передаточных отношений по ДЧВ с линией редукции АИКЗД, где первое передаточное отношение максимальное, а остальные – минимально возможные. Однако в этом случае частота вращения II вала nII будет в два раза выше nдв и при значительном nII окружные скорости колес могут оказаться больше допустимых, возрастёт опасность вибраций. При больших частотах вращения возрастают требования к системе смазки и т.д.
С учётом отмеченных конструктивного и динамического факторов оптимальным будет являться вариант ДЧВ с линией редукции АЕЖЗД, в которой i1>i2>i3>i4.
2) Ременная передача плохо работает на низких скоростях, поэтому её одну без переборного устройства не используют в качестве шпиндельной передачи. Передаточное отношение ременной передачи берется от 1/4 до 1, т.к. она хорошо работает на замедление и плохо на ускорение.
Поэтому в приводе ременную передачу часто используют для связи электродвигателя с первым валом коробки скоростей и делают её замедляющей (на рис. 3.2 – i1).
3.9.3 Расчёт чисел зубьев передач групп
Числа зубьев некоррегированных колёс, исходя из условия отсутствия подрезания при их изготовлении и из конструктивных соображений, не следует принимать менее
Zmin=(17-)20-22.
Числа зубьев в группе передач, содержащей шестерни одинакового модуля, можно определить различными способами, и в том числе:
- способом наименьшего общего кратного;
- упрощенным способом;
- с помощью логарифмической линейки;
- по специальным таблицам.
Рассмотрим суть упрощенного способа расчёта чисел зубьев.
Пусть в группе передач 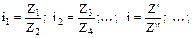 при этом
при этом 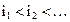 и
и
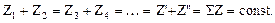 Т.к.
Т.к. 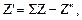 а
а 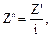
то 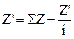 или
или 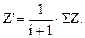 Приняв
Приняв 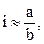 получим:
получим:
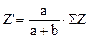 и
и 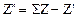 (3.1)
(3.1)
При расчёте чисел зубьев принимают Z1=Zmin, определяют 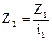 и SZ=Z1+Z2; обычно SZ£120. Затем определяют все остальные числа зубьев по формулам (3.1).
и SZ=Z1+Z2; обычно SZ£120. Затем определяют все остальные числа зубьев по формулам (3.1).
Пример. Определить числа зубьев передач группы на три скорости, представленной на фрагменте ДЧВ (рис. У.13,а), φ=1,26.
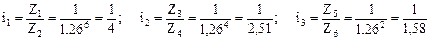 .
.
Принимаем Z1=20, тогда Z2=20:(1/4)=80 и SZ=20+80=100;
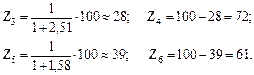
Подсчитанные числа зубьев проставляем на ДЧВ рис. У.13.б).
а) б)
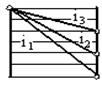 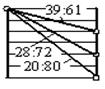 Рис. У.13. Фрагменты ДЧВ: а – до расчёта чисел зубьев; б – с проставленными числами зубьев
Рис. У.13. Фрагменты ДЧВ: а – до расчёта чисел зубьев; б – с проставленными числами зубьев
| 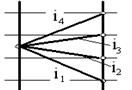 Рис. У.14а. Фрагмент ДЧВ для сменных обратимых шестерён
Рис. У.14а. Фрагмент ДЧВ для сменных обратимых шестерён
|
3.9.4 Особенности расчёта приводов со сменными обратимыми зубчатыми колёсами
При использовании в приводе сменных колёс (см. п/п. 2.2.4.1 и рис. У.5) можно уменьшить их количество, сделав обратимыми, т.е. обеспечив с помощью, например, двух колёс Z1¹Z2 (а¹б) два передаточных отношения
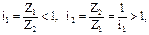 с помощью 4 колёс – 4 и т.д.
с помощью 4 колёс – 4 и т.д.
На ДЧВ группа из сменных обратимых колёс имеет симметричные лучи. Фрагмент ДЧВ для группы на четыре варианта из обратимых сменных шестерён показан на рис. У.14а. Передаточные отношения группы будут следующими:
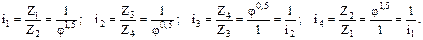
В данном случае 2 пары сменных обратимых колёс являются основной группой.
Суммы зубьев сменных колёс для станков принимают обычно равными 72, 90 или 120.
3.9.5 Особенности расчёта приводов с многоскоростными электродвигателями
Применение в приводе многоскоростного электродвигателя позволяет несколько упростить механическую часть привода и обеспечить возможность переключения скоростей на ходу.
При расчёте коробок скоростей такой двигатель играет роль первой в кинематическом плане группы передач, т.е. рассматривается как некая фиктивная "электрогруппа" со знаменателем jэ=jр, где р – произведение чисел передач групп, предшествующих "электрогруппе" по порядку переключения для обеспечения последовательно возрастающего геометрического ряда частот вращения шпинделя.
Правильный геометрический ряд частот вращения шпинделя может быть получен при применении электродвигателей с jэ=2. К таким относятся асинхронные электродвигатели, у которых синхронные частоты вращения равны 750/1500; 1500/3000; 750/1500/3000.
С учётом отмеченного 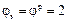 , откуда
, откуда 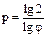 .
.
Решение последнего выражения для ряда значений φ дано ниже:
| φ: | 1,06; | 1,09; | 1,12; | 1,18; | 1,26 (1,25); | 1,41 (1,4); | |
| p: | 12; | 8; | 6; | 4; | 3; | 2; |
Очевидно, "электрогруппа" при φ <2 должна быть множительной группой. К примеру, при φ=1,26 и 1,41 она должна быть I множительной с числом передач в основной 3 и 2 соответственно.
Пример. Построить структурную сетку для привода 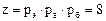 с двухскоростным электродвигателем и φ =1,41.
с двухскоростным электродвигателем и φ =1,41.
При φ =1,41 "электрогруппе" должна предшествовать по порядку переключения основная группа на две скорости. Примем структурный вариант 8=2(2)·2(1)·2(4) и построим для этого случая структурную сетку (рис. У.14б), предварительно проверив, какое φmax допускается выбранной структурой и возможна ли её реализация при заданном φ.
Итак 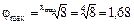 и реализация структуры при φ =1,41 возможна.
Минимальное передаточное отношение привода будет равно: и реализация структуры при φ =1,41 возможна.
Минимальное передаточное отношение привода будет равно:
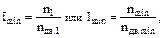 где nдв.min – минимальная частота вращения вала многоскоростного электродвигателя.
Примечание. На сетке (см. рис. У.14б) пунктиром показана часть, относящаяся к группе 2(2), которой на самом деле нет, а есть лишь две частоты вращения вала электродвигателя nдв.1 и nдв.2. В связи с этим то, что показано пунктиром, обычно на структурных сетках и ДЧВ не изображается.
где nдв.min – минимальная частота вращения вала многоскоростного электродвигателя.
Примечание. На сетке (см. рис. У.14б) пунктиром показана часть, относящаяся к группе 2(2), которой на самом деле нет, а есть лишь две частоты вращения вала электродвигателя nдв.1 и nдв.2. В связи с этим то, что показано пунктиром, обычно на структурных сетках и ДЧВ не изображается.
| 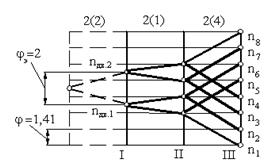 Рис. У.14б. Построение структурной сетки
для привода с многоскоростным
электродвигателем
Рис. У.14б. Построение структурной сетки
для привода с многоскоростным
электродвигателем
|
Дата добавления: 2016-02-20; просмотров: 5334;
