Применение составных (ломаных) геометрических рядов

В станках средняя часть диапазона скоростей шпинделя используется чаще, чем его крайние значения. В связи с этим можно проектировать структуры с составным (ломаным) геометрическим рядом, т.е. рядом, имеющим в различных интервалах неодинаковые знаменатели.

Удобно использовать ломаные ряды со знаменателем φ_б для крайних и 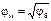для средних ступеней диапазона частот вращения шпинделя.

В качестве φ_б и φ_м могут быть приняты следующие знаменатели основных рядов 1,58 и 1,26; 1,26 и 1,12; 1,12 и 1,06; а также выборочных 2,5 и 1,58; 2 и 1,41; 1,41 и 1,18; 1,18 и 1,09.

Один из способов проектирования привода с составным (ломаным) геометрическим рядом следующий: уменьшают характеристику последней множительной группы по сравнению с расчётной величиной на 0,5·u, где u = 1, 3, 5, 7, ... – какое-либо нечетное число.

То есть x_k.лом=x_k–0,5·u. При p_k=2 x_k=z/2 и x_k.лом=(z–u)/2.

На структурной сетке или ДЧВ u равно числу интервалов ряда частот вращения со знаменателем φ_м, т.е. u+1 частот вращения шпинделя составляет ряд со знаменателем φ_м.

Пусть, к примеру, z=12, u=7, тогда х_k.лом =(12–7)/2=2,5 и z=12=3(1)·2(3)·2(2,5).

Структурная сетка для этого случая показана на рис. 3.5. На ней лучи передач последней группы проведены несколько несимметрично с целью упрощения построения сетки.

Диапазон регулирования привода с ломаным геометрическим рядом

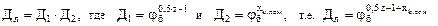
или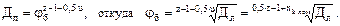

x_max и φ_б.max следует определять в k-той и (k–1)-й множительных группах и φ_б принимать не превосходящим меньшего из двух найденных φ_б.max.

Значения φ_б.max для ряда x_max даны в таблице на рис. 3.1,ж и 3.5,б.

В рассматриваемом примере:

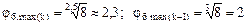и можно принять .

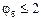При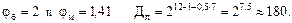

Для сравнения: нормальная множительная структура на 12 вариантов 12=3(1)·2(3)·2(6) при 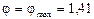обеспечивает 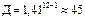, что в 4 раза меньше.