Основные газовые законы.

Сила взаимодействия между молекулами, как известно, зависит от расстояния между ними. Силы межмолекулярного взаимодей­ствия (так называемые силы когезии) за пределами расстояния, большего 10^{-7 см от центра молекулы, настолько ослабевают, что ими можно пренебречь.}

Средней кинетической энергии теплового движения молекул газа вполне достаточно, чтобы преодолеть силы когезии (силы межмолекулярного взаимодействия). При столкновении молекул друг с другом, когда одна молекула попадает в силовое поле при­тяжения другой молекулы, между ними возникает мгновенное когезионное взаимодействие.

Чем больше давление, тем больше число столкновений молекул газа в 1 с, а следовательно, и суммарные мгновенные когезионные взаимодействия между ними оказывают большее влияние на свой­ства данного газа. И наоборот, в состоянии сильного разрежения размеры молекул по сравнению с межмолекулярными расстояния­ми и силы взаимодействия между молекулами ничтожны.

В силу хаотического движения молекул газа концентрация их в любой части занимаемого газом пространства одинакова, как и плотность его во всей массе.

Однако это справедливо лишь в том случае, если речь идет о средней плотности газа в макрообъеме. В микрообъеме же вслед­ствие хаотичности молекулярного движения могут происходить значительные отклонения от средней плотности. Это явление назы­вается флуктуацией (лат. fluctuatio — колебание). Флуктуационные отклонения плотности тем больше, чем меньше микрообъем. В отдельных случаях они могут достигать 20% и более по сравне­нию со средней плотностью газа во всей его массе.

Газы широко распространены в природе и используются в раз­личных отраслях народного хозяйства в качестве топлива, тепло­носителей, сырья для химической промышленности, рабочего тела для выполнения механической работы (газовые турбины) и во мно­гих других случаях. Отсюда вытекает необходимость знания зако­нов, которым подчиняются газы.

Основные газовые законы выведены для идеального газа. Иде­альным называется газ, находящийся в таком состоянии, при ко­тором можно пренебречь силами межмолекулярного взаимодей­ствия и собственным объемом его молекул.

Свойства идеального газа, таким образом, определяются тем­пературой и давлением, при которых газ находится в данный мо­мент.

Газы, реально существующие в природе (реальные газы), в большей или меньшей степени отступают от газовых законов.

Закон Бойля-Мариотта. Объем данной массы газа (V) при постоянной температуре изменяется обратно пропорционально дав­лению (р), под которым газ находится:

1.1

или p₁V₁ = p₂V₂. Аналогичное равенство можно написать и для дру­гих значений р и V:

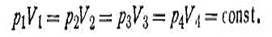
1.2

Отбросив индексы, получим:

1.3

при условии, что t = const.

Таким образом, произведение объема газа на его давление при постоянной температуре есть величина постоянная. Величина кон­станты в уравнении (1.2) зависит от природы газа, его количества и температуры, но не зависит от изменения объема или изменения давления.

Из закона Бойля-Мариотта вытекает следующее: концентра­ция и плотность данной массы газа изменяются при постоянной температуре прямо пропорционально изменению давления и обрат­но пропорционально изменению объема.

Таким образом, исходя из уравнения (1.1) можно записать:

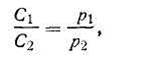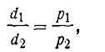
1.4

где С₁, С₂ и d₁,d₂ - соответственно концентрации и плотности дан­ной массы газа.

Закон Гей-Люссака. При нагревании данной массы газа на 1 К при постоянном давлении объем его увеличивается на 1/273,16 часть того объема, каким обладал бы газ при 273,16 К и при том же давлении. Так, если объем газа при 273,16 К был V₀, при нагре­вании газа на ∆T градусов стал Vт, а прирост объема ∆V, то

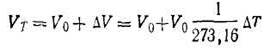
1.5

Или

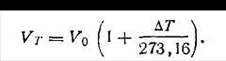
1.6

В уравнении (1.6) величина 1/273,16 =a, носит название коэф­фициента термического расширения. Этот коэффициент не зависит от природы идеального газа, его давления, объема и температуры. Таким образом,

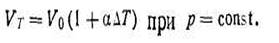
1.7

Если объем газа остается постоянным, то по такому же закону растет и давление:

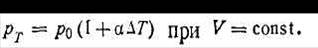
1.8

В этом случае величина a, равная 1/273,16, называется терми­ческим коэффициентом упругости газа.

Математическую зависимость, выражающую закон Гей-Люссака, можно значительно упростить, если в уравнение (1.5) вместо ∆Т ввести Т.

Учитывая, что

1.9

преобразуем уравнение (1.5) следующим образом:

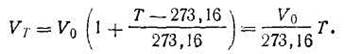
1.10

Отбросив индексы и объединив постоянные величины в одну кон­станту, получим V = const T при р = const. Аналогично можно пре­образовать и уравнение (1.8), получив р = const Т при V = const.

На основании приведенных уравнений можно сделать вывод: объем и давление изменяются прямо пропорционально изменению термодинамической температуры газа:

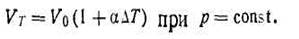
	1.11
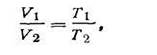
	1.12

Графически закон Гей-Люссака выражается пучком прямых ли­ний, выходящих из начала координат.

Из закона Гей-Люссака вытекает: плотность и концентрация газа, находящегося под постоянным давлением, обратно пропор­циональны термодинамическим температурам

1.13

Закон Авогадро. В равных объемах различных газов при оди­наковой температуре и дав­лении содержится одинако­вое число частиц (молекул или атомов).

Из закона Авогадро вы­текает важное следствие. Число молекул, которое со­держится в одном киломоле любого газа, есть величина постоянная: N₀= 6,02·10²⁶ (постоянная Авогадро).

Полезно отметить, что термин кмоль определяется как 6,02·10²⁶ «формульных единиц» (не обязательно молекул!). Следовательно, при одинаковых условиях 1 кмоль лю­бого газообразного вещества должен занимать постоянный объем. Так, при нормальных условиях (T = 273,16 К; р= 101 325 Па) 1 кмоль любого газа занимает объем 22,4 м³. Этой величиной час­то пользуются в расчетах.

Состояние газа характеризуется тремя величинами: давлением р, объемом V и температурой Т. Эти три величины связаны урав­нением, которое получило название уравнения состояния идеально­го газа.

Оно выводится путем объединения законов Бойля-Мариотта, Гей-Люссака и Авогадро. Если 1 кмоль газа при нормальных усло­виях (р₀, Т₀ и V₀) нагреть до определенной температуры Т при том же давлении, то согласно закону Гей-Люссака объем газа при этой температуре V_T будет равен:

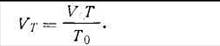
1.14

Если при постоянной температуре Т изменить давление газа от р₀ до любого значения р, то объем газа также изменится и станет равным V. На основании закона Бойля-Мариотта pV = p₀V_Т.

Подставив в это уравнение значение V_Т (I.11),

получим pV = Tp₀V₀ /T₀, откуда

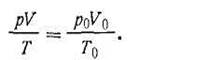
1.15

Поскольку p₀, V₀ и Т₀ — величины постоянные, отношение P_oV_o/T_o есть также величина постоянная для всех газов независимо от их химической природы. Эту постоянную величину обозначают буквой R и называют универсальной газовой постоянной. С учетом этого уравнение (I.15) преобразится:

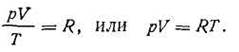
1.16

Уравнение (I.16) справедливо для 1 кмоль газа. Если в объеме газа будет содержаться n кмоль, то это уравнение будет иметь бо­лее общий вид:

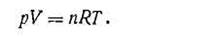
1.17

Уравнение (I.17) является основным уравнением газового со­стояния и называется уравнением Клапейрона - Менделеева. Впервые это уравнение было выведено Клапейроном в 1834 г. Д. И. Менделеев в своих работах в 1874 г. указал, что благодаря закону Авогадро уравнение Клапейрона приобретает наибольшую общность, когда оно относится не к обычной единице массы (грам­му или килограмму), а к 1 кмоль газа.

Число киломолей газа n можно рассчитать по формуле

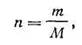
1.18

где m — масса газа, содержащегося в объеме V при давлении р и температуре Т ; М — масса киломоля газа.

Подставив значение n в уравнение (I.17), получим

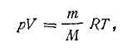
1.19

Откуда

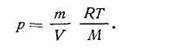
1.20

Отношение m/V есть не что иное, как плотность газа d, откуда d = Mp/RT. Если обе части уравнения (I.20) разделить на объем V, получим

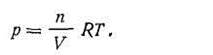
1.21

Поскольку отношение n/V есть концентрация газа С, то уравнение Клапейрона - Менделеева будет иметь вид:

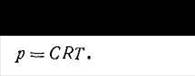
1.22

Численное значение универсальной газовой постоянной зависит от того, в каких единицах измерены нормальное давление р₀ и объем V₀ одного моля таза.