Свойства логарифмов

1. log_b x + log_by = log_b(xy).

2. log_b x – log_by = log_b(x/y).

3. k log_b x = log_b(x^k).

4. b^log_b^x = x.

5. log_ax = (log_ab) ∙ log_bx.

Поскольку 1n10 ≈2,3026 (т.е. натуральный логарифм 10 приблизительно равен 2,3026), по свойству 5 имеем:

ln x ≈ 2,3026 1g х.

Любое число, выраженное в виде десятичной дроби, может быть записано в «стандартной» форме как произведение целой степени 10 и числа между 1 и 10. Так, например, 0,002 = 2 ∙ 10 ^{– 3}; 352 = 3,52 ∙ 10²; 4,32 = 4,32 ∙ 10⁰.

Благодаря свойству логарифмов 1 :

1g 0,002 = 1g 2 + 1g 10 ^{– 3} = 1g 2 – 3;

lg 352 = lg 3,52 + lg 10² = lg 3,52 + 2;

lg 4,32 = lg 4,32 + lg 10⁰ = lg 4,32 + 0.

Эти замечания иллюстрируют общее положение, согласно которому всякий десятичный логарифм можно выразить в виде суммы целого числа и логарифма числа, заключенного между 1 и 10. Последний логарифм сам является числом, заключенным между 0 и 1, и поэтому приближенно может быть выражен положительной десятичной дробью. Эта десятичная дробь на­зывается мантиссой, причем таблицы десятичных логарифмов и представляют собой таблицы мантисс. Показатель степени 10, который входит в стандартную форму числа, называется характеристикой. Таким образом, характеристика числа 0,002 есть – 3, характеристика 352 есть 2, а характеристика 4,32 есть 0.

В вычислениях с логарифмами принято писать отрицатель­ные характеристики в так называемой форме 9 – 10. В этой форме 1g 0,002 = 7,3010 – 10. Данное выражение можно записать также в виде 1g 0,002 = 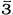,3010, где черта над 3 означает, что характеристика равна – 3, а десятичная часть + 0,3010. Оба равенства означают, что 1g 0,002 = 0,3010 – 3 = – 2,6990.

Пример А.6. Найдем 1g 352.

Решение:

352 = 3,52 ∙ 10²;

1g 352 = 1g 3,52 + 1g 10².

Из таблиц 1g 3,52 = 0,5464, а по определению 1g 10² = 2. Таким образом,

1g 352 = 2 + 0,5464 = 2,5464.

Пример А.7. Найдем 1g 0,002.

Решение:

1g 0,002 = 1g (2 ∙ 10 ^{– 3}) = 1g 2 + lg 10 ^{– 3} = 0,3010 + (–3) = – 2,6990.

Пример А. 8. рН раствора представляет собой отрица­тельный десятичный логарифм [Н⁺], где [Н⁺] — активность ионов водорода (приблизительно равная концентрации ионов водорода, выраженной в г–ион/л), т.е. рН = – 1g[Н⁺]. Найдем, чему равен рН раствора, если [Н⁺] = 0,000243.

Решение:

рН = – 1g (0,000243) = – 1g (2,43 ∙ 10 ^{– 4}) = – (0,386 – 4) = 3,614.

Для того чтобы найти число по известному логарифму, можно использовать аналогичный подход.

Пример А. 9. Найдем [Н⁺], если рН = 2,602.

Решение:

– lg [Н⁺] = 2,602

1g [Н⁺] = – 2,602 = 0,398 – 3.

Из таблиц находим, что 0,398 = 1g 2,5, поэтому

[Н⁺]=2,5 ∙ 10 ^{– 3} = 0,0025.

Перед тем как обратиться к таблицам, мы выразили – 2,602 в виде суммы положительной десятичной дроби и целого числа – 3, поскольку таблицы содержат только положительные десятичные дроби.

Пример А. 10. Для того чтобы найти рН, с помощью рН – метра измеряют электрическое напряжение ξ и по формуле рН = ξ – 0,336/ 0,059 получают величину рН.

Найдем [Н⁺], если ξ = 0,525.

Решение:

ξ = 0,525 – 0,336/0,059 = 3,20.

–lg[Н⁺] = 3,20,

lg[Н⁺] = – 3,20 = 0,80 – 4,

[Н⁺] = 6,3 ∙ 10^-4.

Пример А. 11. Для того же рН – метра, что и в преды­дущем примере, определим, какое значение ξ соответство­вало бы концентрации ионов водорода 2,3 ∙ 10 ^{– 7}.

Решение:

рН = – 1g [Н⁺] = – 1g (2,3 ∙ 10 ^{– 7}) = – (0,3617 – 7) = –(– 6,6383) = 6,6383.

Подставляя полученное значение рН в формулу, приведен­ную в примере А. 10, находим ξ :

ξ – 0,336/0,059 = 6,638;

ξ = 0,059 ∙ 6,638 + 0,336 = 0,728.