Основные требования к построению математических структурных моделей
Часто объектом изучения в математике служит множество вместе с определенной на нем структурой, например: множество треугольников с отношением подобия, множество вещественных функций со свойством линейности и операцией дифференцирования, множество узлов и сетевых элементов ТК-систем со своими взаимосвязями и другие. В математической логике уточняется понятие структуры, заданной на множестве, с помощью таких понятий как алгебраическая система и сигнатура.
Определение. Упорядоченная тройка  называется сигнатурой, если выполняются следующие условия:
называется сигнатурой, если выполняются следующие условия:
а) множества  и
и  не имеют общих элементов;
не имеют общих элементов;
б) 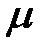 - местная операция, которая задается на множестве
- местная операция, которая задается на множестве  .
.
Для того чтобы построить модель 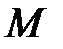 непротиворечивой теории
непротиворечивой теории  алгебраической системы
алгебраической системы  сигнатуры
сигнатуры 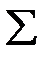 , необходимо:
, необходимо:
1) на множестве 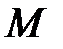 задать алгебраическую систему
задать алгебраическую систему 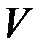 сигнатуры
сигнатуры 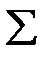 ;
;
2) установить изоморфизм  :
:  , т.е. доказать, что алгебраические системы
, т.е. доказать, что алгебраические системы  и
и  изоморфны.
изоморфны.
Рассмотрим строгое обоснование построения математической модели ТК-системы – матрицы инциденций с позиций теории моделей. Обозначим элементы ТК-системы  через
через  , где
, где  принимает значения 1,2,…,
принимает значения 1,2,…,  , коммутации через
, коммутации через  ,
, 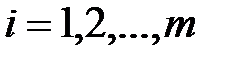 . Сигнатуру
. Сигнатуру  ТК-системы
ТК-системы 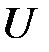 определим следующим образом:
определим следующим образом: 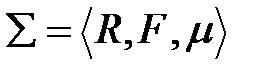 ,
, 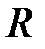 - множество элементов ТК-системы,
- множество элементов ТК-системы, 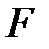 - множество коммутаций. В качестве местной операции
- множество коммутаций. В качестве местной операции  возьмем свойство инцидентности:
возьмем свойство инцидентности:

Рассмотрим ТК-систему 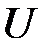 как алгебраическую систему сигнатуры
как алгебраическую систему сигнатуры 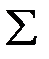 . Построим модель ТК-системы
. Построим модель ТК-системы 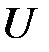 следующим образом. Пусть
следующим образом. Пусть  , тогда
, тогда 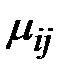 можно рассмотреть как элементы матрицы, которая называется матрицей инциденций. Таким образом, любому элементу
можно рассмотреть как элементы матрицы, которая называется матрицей инциденций. Таким образом, любому элементу  ТК-системы
ТК-системы 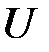 из множества
из множества  и любой коммутации
и любой коммутации 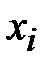 из
из  мы ставим в соответствие элемент
мы ставим в соответствие элемент  матрицы инциденций, т.е. нами установлен гомоморфизм алгебраической ТК-системы
матрицы инциденций, т.е. нами установлен гомоморфизм алгебраической ТК-системы 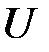 сигнатуры
сигнатуры  на матрицу
на матрицу 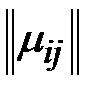 той же сигнатуры
той же сигнатуры 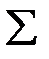 . Каждому элементу
. Каждому элементу 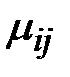 матрицы инциденций можно поставить в соответствие элемент ТК-системы
матрицы инциденций можно поставить в соответствие элемент ТК-системы  и коммутацию
и коммутацию 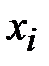 , т.е. установлен и обратный гомоморфизм. Следовательно, ТК-система
, т.е. установлен и обратный гомоморфизм. Следовательно, ТК-система 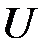 изоморфна матрице инциденций
изоморфна матрице инциденций 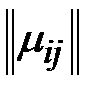 , т.е. матрица инциденций является строго обоснованной адекватной математической моделью ТК-системы, однако описанная модель, как и любая другая, далеко не совершенна, ибо в общем случае не обладает свойствами инвариантности. Кроме того, результаты спектрального анализа этих матриц имеют ограниченную применимость в силу того, что компоненты их спектра зависят не только от состояния отдельных направлений, но и от порядка нумерации элементов графа сети.
, т.е. матрица инциденций является строго обоснованной адекватной математической моделью ТК-системы, однако описанная модель, как и любая другая, далеко не совершенна, ибо в общем случае не обладает свойствами инвариантности. Кроме того, результаты спектрального анализа этих матриц имеют ограниченную применимость в силу того, что компоненты их спектра зависят не только от состояния отдельных направлений, но и от порядка нумерации элементов графа сети.
Рассмотрим конкретные типы моделей.
4.5. Математические модели типа „черного ящика”
Во многих случаях структура системы априори не известна или сама система является слабо структурированной. В этом случае систему 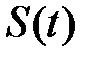 представляют в виде двух-, четырех- или
представляют в виде двух-, четырех- или  -полюсника с соответствующими входами
-полюсника с соответствующими входами  и выходами
и выходами  . Такое представление носит название „черного ящика” (рис.4.2). В данной системе
. Такое представление носит название „черного ящика” (рис.4.2). В данной системе  изучаются влияния входных сигналов
изучаются влияния входных сигналов  на выходные
на выходные  , то есть анализируются причинно-следственные связи без конкретизации ее внутренней структуры. В простейшем линейном представлении (1 вход, 1 выход) эта связь имеет вид
, то есть анализируются причинно-следственные связи без конкретизации ее внутренней структуры. В простейшем линейном представлении (1 вход, 1 выход) эта связь имеет вид
 . (4.4)
. (4.4)
В случае  -входов и
-входов и 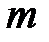 -выходов функции
-выходов функции 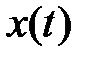 и
и 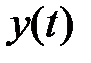 являются векторами, а
являются векторами, а 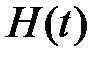 - матрицей.
- матрицей.
В более сложных нелинейных системах 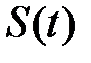 - это представление (4.4) нелинейно
- это представление (4.4) нелинейно
 .
.
Матрица  и функция
и функция  носят название передаточных функций системы
носят название передаточных функций системы 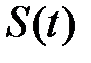 .
.
| выход |
| вход |

|
 
|
| S(t) |
Рис. 4.2. Пример системы  в виде «черного ящика»
в виде «черного ящика»
с  -входами
-входами 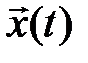 и
и  -выходами
-выходами 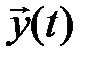
С помощью передаточной матрицы  можно моделировать электрические схемы, устройства, узлы и каналы связи и др. Наиболее распространенным является представление векторного канала связи. Так, в задачах пространственно-временного кодирования (MIMO – много входов, много выходов), используемого в системах Wi-Fi, Wi-MAX, на передающей стороне может излучаться несколько пространственно-разнесенных информационных сигналов, а на приемной – осуществляться их прием на
можно моделировать электрические схемы, устройства, узлы и каналы связи и др. Наиболее распространенным является представление векторного канала связи. Так, в задачах пространственно-временного кодирования (MIMO – много входов, много выходов), используемого в системах Wi-Fi, Wi-MAX, на передающей стороне может излучаться несколько пространственно-разнесенных информационных сигналов, а на приемной – осуществляться их прием на 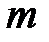 -антенн. Передавая периодически известные тестовые сигналы, находят значения передаточных функций
-антенн. Передавая периодически известные тестовые сигналы, находят значения передаточных функций 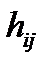 (BLAST-алгоритм). Это позволяет на интервале между тестами считать канал связи с известными параметрами, что, в конечном счете, обеспечивает бóльшую пропускную способность и надежность связи. Очевидно, вместо или одновременно с пространственным разнесением можно использовать и поляризационное. В этом случае входные
(BLAST-алгоритм). Это позволяет на интервале между тестами считать канал связи с известными параметрами, что, в конечном счете, обеспечивает бóльшую пропускную способность и надежность связи. Очевидно, вместо или одновременно с пространственным разнесением можно использовать и поляризационное. В этом случае входные 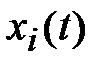 и выходные
и выходные  , компоненты рассматривают как ортогонально-поляризованные составляющие электромагнитного поля.
, компоненты рассматривают как ортогонально-поляризованные составляющие электромагнитного поля.
Однако модель «черного ящика» является упрощенной. Так для динамических систем, где внутренняя структура и ее состояния изменяются во времени требуется детальная конкретизация. Часто используют одновременно две модели: композицию модели наблюдения в виде черного ящика и динамической модели состояния, описываемой системой дифференциальных уравнений (рис. 4.3).
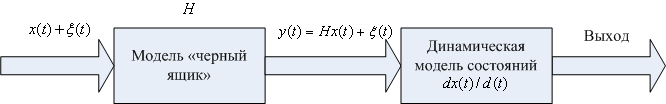
Рис. 4.3. Составная модель наблюдения  и состояния
и состояния 
При этом модель «черного ящика» по отношению модели состояний играет роль модели наблюдения, где 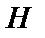 матрица усиления,
матрица усиления,  - помехи.
- помехи.
Дата добавления: 2016-02-20; просмотров: 953;
