Формализация моделей систем

Формализация – это процедура представления и изучения какой-либо области знаний в виде определенного вида вычислений. Формализация основывается на методах формальной логики и математических методах научных исследований.

Для формализации используются искусственные языки, которые характеризуются точными правилами построения выражений и их понимания. Основным формализованным языком является логико-математический, который объединяет математическую и логическую символику. Формализованный язык основывается на алфавите, то есть на перечне символов (букв), из которых строятся все выражения языка, и синтаксисе – правилах построения определенных выражений.

Для обозначения конкретных объектов используются переменные и константы, которые называются термами. Например, выражение 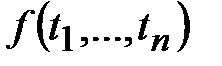– представляет собой n-местный функциональный символ, являющийся термом. Термами являются также переменные 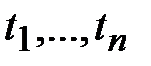. Из термов с помощью предикатных символов и символов логических операций строятся формулы – выражения, соответствующие высказывания.

Символами логических операций являются знаки: 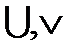– дизъюнкции, 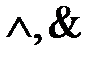– конъюнкции, 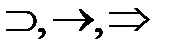– импликации, – отрицание, а также кванторы: "– обобщения и $ – существования.

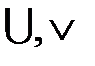– дизъюнкция (латинское слово, означает отличие) – логическая операция; заключается в соединении двух высказываний 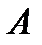и В в новое высказывание А или В. Изображается: , читается: А или B, а также имеет место А или имеет место В, то есть истинное хотя бы одно из них: B или .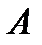

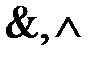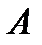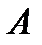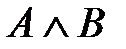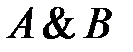– конъюнкция (латинское слово, обозначающее союз, связь) – логическая операция; заключается в соединении двух высказываний и B в новое высказывание и B. Изображается: или 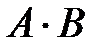, или , или 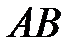. Читается 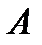и B, а также имеет место 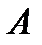,и имеет место B; то есть высказывание 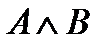истинно только при истинности обоих высказываний 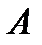и B одновременно.

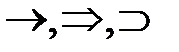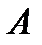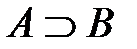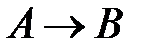– импликация (латинское слово, означает: сплетение, тесная связь), логическая операция; заключается в соединении двух высказываний и B в новое высказывание если А, то B. Изображается: или , или 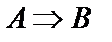. Читается, если А, то B; А вызывает B. Высказывание А называется посылкой высказывания, B – его окончанием. В данном случае рассматривается причинная связь между 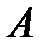и B: если А истинно и B – истинно, то 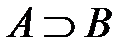– истинно, если А – истинно, а B – неистинно, то 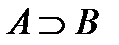– неистинно, если A–неистинно, а B – истинно, то 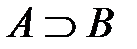– истинно, если А – неистинно и B – неистинно, то 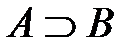– истинно.

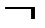– отрицание, логическая операция, в результате которой из данного высказывания 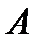получается новое высказывание не .

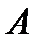– квантор обобщения (латинское слово, означает сколько). 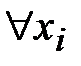значит, что для всех ....

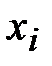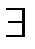– квантор существования, 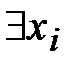означает, что “для некоторых 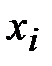... ” или “существует ... ”

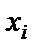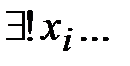– квантор единства. означает, что “для одного и только для одного …”.

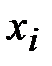Предикатными символами (предикат – латинское слово, означает сказанное) являются такие символы, которые служат для формализации логических выводов, в которых учитывается как логическая структура суждений (то есть, каким образом данное суждение получено из других с помощью логических операций), так и их субъективно выраженная структура, между субъектами суждения (о чем говорится в данном суждении) и предикатом (что говорится о субъекте). Предикатом является функция высказывания, определенная на некотором множестве 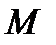, то есть n-местнаяфункция P, которая каждому упорядоченному набору 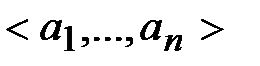элементов множества ставит в соответствие некоторое высказывание, изображаемое как 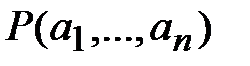. При этом 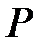– называется n-местнымпредикатом на 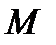. Например, предикатом может быть логическая последовательность действий по переводу ТК-системы в состояние или режим, где термы 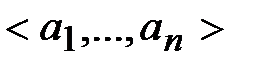обозначают соответствующие упорядоченные действия.

Сейчас в математике чаще всего применяется формализованный логико-математический язык на основе алфавита, буквами которого являются символы логических операций и кванторы, а также функциональные символы сложения и умножения.

Формализованный язык разделяется на два основных уровня или порядка. Если язык первого порядка представляется в некотором смысле элементарно, то в языках второго порядка могут использоваться предикатные и функциональные переменные и кванторы при таких переменных, а также предикатные и функциональные символы второго порядка, примененные к обычным функциональным и предикатным символам. Примером таких символов второго порядка являются операторы возведения в степень, интеграции, дифференцирования и др.

Проблема формализации модели включает в себя следующие основные этапы: замыкание, структуризацию, параметризацию, описание. Рассмотрим эти этапы более детально.

4.3.1. Замыкание системы – это неформальное, субъективное выделение, вычленение той достаточной части окружающего мира, которую можно назвать системой и рассматривать самостоятельно без связи с окружающей средой. Процедура замыкания системы зависит от практических потребностей. Один и тот же объект в зависимости от задачи может считаться замкнутой или разомкнутой (открытой) системой.

Окружающий мир 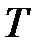можно представить как некоторую метасистему множеств, состоящую из взаимодействующих 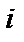-систем 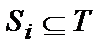, которая сама представляет замкнутую систему:

.

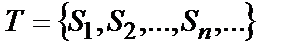
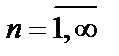4.3.2. Структуризация системы – построение модели в виде элементов и связей.

На этапе структуризации осуществляется выявление в системе отдельных элементов и связей между этими элементами. Встречаются системы с хорошей или четкой структурированностью, например, телекоммуникационная сеть, которая включает узлы (элементы), объединенные линиями связи. В то же время включение в нее облачной компоненты приводит к слабой или нечеткой структурированности. Вместе с тем, модель организационно-штатной структуры ТК-системы может быть определена достаточно четко.

Структурные свойства ТК-систем адекватно отображаются с помощью теории графов, структура при этом образует сеть.

Структурой системы определяется множество бинарных отношений между элементами системы S. Очевидно, структура 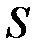отображается на множестве расположений элементов системы :

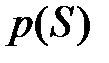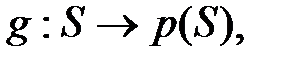
где 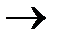означает знак отображения 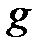. Это отображение может быть определено для каждого элемента 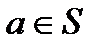, поскольку существует 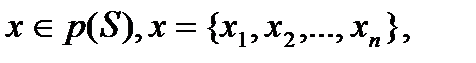элементы которого 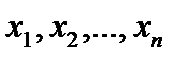формируют пары в данной структуре D:

.

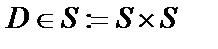Очевидно, в структуре D нево всех парах 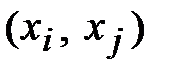определено значение 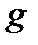, отличное от нуля. Если же 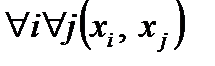существует отличное от нуля значение, то такая структура является полносвязной. Данные связи могут быть постоянны, при постоянном закреплении каналов, или переменными, как в системах связи с коммутацией каналов.

Структурные связи, образующие множество бинарных отношений между элементами системы, обладают свойствами симметричности, рефлексивности и транзитивности. Симметричность бинарных отношений между 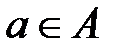и 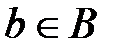обеспечивается в том случае, когда 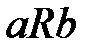вызывает 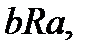что в применении к бинарным отношениям между элементами в системе связи отвечает наличие прямых и обратных каналов между соответствующими узлами.

Рефлексивность бинарных отношений – это такое свойство, которое удовлетворяется для каких-либо пар объектов с совпадающими членами, то есть, 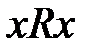для 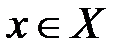. Очевидно, все пары дуплексных каналов с одинаковыми качественными показателями рефлексивны.

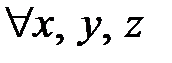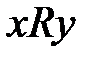Транзитивность (латинское слово, означает переходный) бинарных отношений – это свойство перенесения этих отношений с одних пар на другие: отношение называется транзитивным, если с и 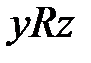следует 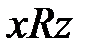. Каналы связи, ретранслируемые на каком-либо узле с сохранением качественных параметров, имеют свойства транзитивности.

4.3.3. Параметризация модели системы– процесс выбора соответствующих объективных показателей, с помощью которых можно отображать состояние системы, принимать решения, осуществлять выбор оптимальных свойств системы и ее элементов. Так, для ТК-систем эти параметры определяют такие свойства, как помехозащищенность, надежность, пропускная способность, мобильность, живучесть и др. Отдельные параметры систем обычно функционально или по вероятности связаны между собой и представляются уравнениями, таблицами или графиками. Для динамических систем состояния представляются дифференциальными уравнениями. Параметризации подлежат как структурные, так и функциональные свойства.

Изучение структурных свойств систем вместе с функциональными (поведенческими, бихейворальными) свойствами являются предметом структурно-функционального анализа, что является основным принципом системных исследований.

Возможен также так называемый непараметрический подход в моделировании систем, который часто используется в статистических задачах (задачи непараметрической статистики, определения непараметрических критериев принятия решений, инвариантность критериев и решений и др.). Однако основное применение данный подход нашел пока еще в задачах, где рассматриваются простые или малые системы. Для сложных систем его применение не очевидно.

4.3.4. Описание модели системы– последний этап формализации модели, когда выбирается формализованный язык, который дает возможность удобно исследовать состояния, функциональные и логические связи, имеющие место в системе. Выбранное средство формализации должно допускать адекватный перевод на удобный язык машинного программирования, что является необходимым для проведения достаточно полного и глубокого анализа рассматриваемой системы. Однако часто ограничиваются и не формализованными описаниями моделей систем. Такими являются дескриптивные (латинское слово, что означает – описательные) модели, где сама модель является логико-лингвистической конструкцией, которую, например, в терминах предикатов, можно свести к формализованному виду, удобному для перевода на язык машинных программ. Модель может быть представлена таблицей, графиком, наконец, она может быть просто объяснена словами. В последнем случае модель называется вербальной (латинское слово, означает – словесный).