Статические и динамические модели

Открытые системы по разному реагируют на одинаковые входные воздействия (см. категорию сложность поведенческая). Эти воздействия можно разделить на управляющие (полезные) и возмущающие (вредные) (рис.4.1).

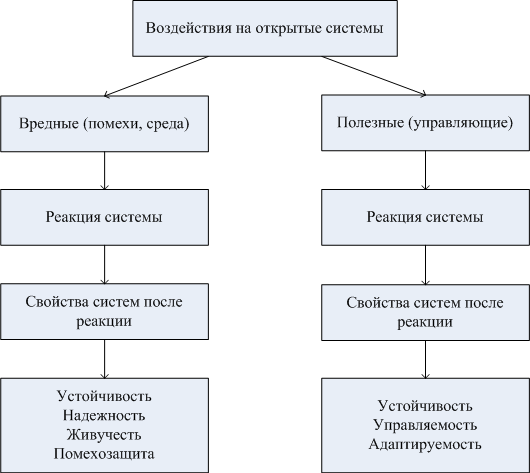
Рис.4.1. Содержание реакции открытых систем на различные внешние воздействия

К вредным воздействиям относятся электромагнитные (естественные или искусственные помехи; помехи, определяющие электромагнитную совместимость); информационные (вирусы, спам); физические (удары, тепло) и др. Борьбе с вредными воздействиями посвящены многие самостоятельные научные теории.

По характеру реакции на воздействия все системы разделяются на два вида – статические (безынерционные) и динамические (инерционные). Когда изучается способность системы реагировать на входные воздействия, то выступает такое свойство как причинность.

Статические системы. Система 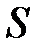называется статической (безынерционной) тогда и только тогда, когда значение ее выходной реакции в любой момент времени зависит исключительно от текущего значения входного воздействия и состояния , с которого началась эволюция системы. При этом, если снимаются входные воздействия , когда , такая система немедленно переходит в начальное равновесное состояние. С использованием логических операций статическая система определяется выражением

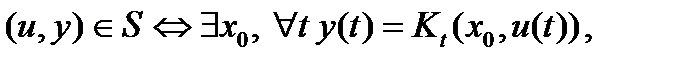(4.1)

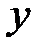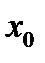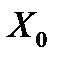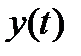что интерпретируется следующим образом: система, у которой определенные значения входов и выходов ( и ), будет тогда и только тогда статической системой S, когда существует начальное состояние , которое принадлежит к множеству возможных начальных состояний и для всех моментов времени выходная реакция определяется начальным состоянием 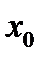и входными воздействиями 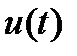, которые обеспечивают отображение 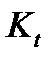в эту выходную реакцию .

Другими словами в статической безынерционной системе S отсутствуют переходные режимы при возникновении или исчезновении воздействий, возмущающих эту систему на входе. Не следует путать со статическим равновесным состоянием инерционной или динамической системы, которая находится в состоянии покоя после переходных процессов, в которых скорость . Статические системы являются определенной абстракцией и альтернативой реальным системам, которым присущи инерционность и динамические переходные режимы. Часто статические системы являются одновременно и системами без памяти (инвариантными), то есть системами, в которых наличие или отсутствие начальных состояний 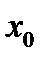не играет роли и соответственно . Несмотря на определенную ограниченность модели статических систем часто используются для анализа стационарных состояний. Математические модели случайных статических систем отображают состояние постоянных параметров, которые могут быть неизвестны, случайны. Случайные статические системы представляются в терминах теории вероятностей, то есть моделями случайных событий и случайных величин.

Динамические системы.Динамической называется инерционная (нестатическая) система, у которой определены функции перехода состояний и исходной реакции , когда . Они бывают стационарными и нестационарными.

Стационарными динамическими называют класс динамических систем, состояние и структура которых не зависит от того, в какой момент времени будет рассматриваться воздействие. О них говорят, что эти системы инвариантны относительно временного сдвига:

(4.2)

то есть для каждого момента времени можно определить оператор сдвига времени 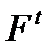такой, что реакция системы на входное воздействие в момент времени зависит лишь от разницы между временем его начала и текущим временем, а не от текущего времени, при этом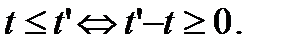

Для стационарной системы , где 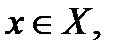, воздействие и реакция являются стационарными, если

(4.3)

Важным свойством стационарных систем является то, что функцию перехода состояния для любого момента времени можно получить как результат применения оператора сдвига к начальной реакции системы.